The document discusses the longest common subsequence (LCS) problem and how to solve it using dynamic programming. It begins by defining LCS as the longest sequence of characters that appear left-to-right in two given strings. It then describes solving LCS using a brute force method with exponential time complexity and using dynamic programming with polynomial time complexity. Finally, it provides an example of finding the LCS of two strings and discusses applications and references.

1. Longest Common
Subsequence Using
Dynamic Programming
Submitted By:
Swati Nautiyal
Roll No.162420
ME-CSE(R)
Submitted To:
Mrs. Shano Solanki
(Assistant Professor CSE)

2. Contents
•Difference in substring and subsequence
•Longest common subsequence
•LCS with brute force method
•LCS with dynamic programming
•Recursion tree of LCS
•LCS example
•Analysis of LCS
•Applications
•References

3. Substring and Subsequence
A substring of a string S is another string S ′ that occurs
in S and all the letters are contiguous in S
E.g. Amanpreet
substring1 : Aman substring2 : preet
A subsequence of a string S is another string S ′ that
occurs in S and all the letters need not to be contiguou
s in S
E.g Amanpreet
subsequence1 : Ant subsequence2 : mnet

4. Longest Common Subsequence
The Longest Common Subsequence (LCS) problem is
as follows. We are given two strings: string A of length x
and string B of length y. We have to find the longest
common subsequence: the longest sequence of
characters that appear left-to-right in both strings.
Example, A= KASHMIR
B= CHANDIGARH

5. Longest Common Subsequence
The Longest Common Subsequence (LCS) problem is
as follows. We are given two strings: string A of length x
and string B of length y. We have to find the longest
common subsequence: the longest sequence of
characters that appear left-to-right in both strings.
Example, A= KASHMIR
B= CHANDIGARH
LCS has 3 length and string is HIR

6. Brute Force Method
Given two strings X of length m and Y of length n, find a longest subse
quence common to both X and Y
STEP1 : Find all subsequences of ‘X’.
STEP2: For each subsequence, find whether it is a subsequence of
‘Y’.
STEP3: Find the longest common subsequence from available
subsequences

7. Brute Force Method
Given two strings X of length m and Y of length n, find a longest subse
quence common to both X and Y
STEP1 : Find all subsequences of ‘X’. 2m
STEP2: For each subsequence, find whether it is a subsequence of
‘Y’. n*2m
STEP3: Find the longest common subsequence from available
subsequences.
T.C= O(n2m)
To improve time complexity, we use dynamic programming

8. Dynamic Programing
Optimal substructure
We have two strings
X= { x1,x2,x3,……,xn}
Y= {y1,y2,y3,…….,ym}
•First compare xn and ym. If they matched, find the subsequence in
the remaining string and then append the xn with it.
•If xn ≠ ym,
• Remove xn from X and find LCS from x1 to xn-1 and y1 to ym
• Remove ym from Y and find LCS from x1 to xn and y1 to ym-1
In each step, we reduce the size of the problem into the subproblems
. It is optimal substructure.

9. Cont.
Recursive Equation
X= { x1,x2,x3,……,xn}
Y= {y1,y2,y3,…….,ym}
C[I,j] is length of LCS in X and Y
{0 ; i=0 or j=0
c[I,j] = 1+c[i-1,j-1] ; I,j>0 and xi=yi
max(c[i-1,j],c[I,j-1]) ; I,j>0 and xi≠yi

10. Recursion Tree Of LCS
BEST CASE
X={A,A,A,A}
Y={A,A,A,A}
C(4,4)
0 ; i=0 or j=0
c[I,j] = 1+c[i-1,j-1] ; I,j>0 and xi=yi
max(c[i-1,j],c[I,j-1]); I,j>0 and xi≠yi
{
1+C(3,3)
1+C(2,2)
1+C(1,1)
1+C(0,0)
0
=1
=2
=3
=4
=4
LCS = 4
T.C. = O(n)

11. Cont.
C(3,3)
C(3,2)
C(3,1)
C(3,0) C(2,1)
C(2,0) C(1,1)
C(1,0) C(0,1)
C(2,2)
C(2,1)
C(2,0) C(1,1)
C(1,0) C(0,1)
C(1,2)
C(1,1)
C(1,0) C(0,1)
C(0,2)
C(2,3)
C(2,2)
C(2,1)
C(2,0) C(1,1)
C(1,0) C(0,1)
C(1,2)
C(1,3)
WORST CASE
X={A,A,A}
Y={B,B,B}
0 ; i=0 or j=0
c[I,j] = 1+c[i-1,j-1] ; I,j>0 and xi=yi
max(c[i-1,j],c[I,j-1]); I,j>0 and xi≠yi
{
As here, the overlapping problem exits, we can apply the dynamic programming.
There are 3*3 unique subproblems. So we compute them once and save in table
for further refrence so n*n memory space required.
No of nodes O(2ⁿ+ⁿ)

12. Cont.
00 01 02 0m
10 11 12 1m
20 21 22 2m
n0 n1 n2 nm
0 1 - - m
0
1
2
-
n
(m+1)*(n+1)
=O(m*n)
Every element is
depend on
diagonal, left or
above element
C(2,2)
C(2,1) C(1,2)
We can compute either row wise or column wise

13. Algorithm
Algorithm LCS(X,Y ):
Input: Strings X and Y with m and n elements, respectively
Output: For i = 0,…,m; j = 0,...,n, the length C[i, j] of a longest string that is a
subsequence of both the strings.
for i =0 to m
c[i,0] = 0
for j =0 to n
c[0,j] = 0
for i =0 to m
for j =0 to n do
if xi = yj then
c[i, j] = c[i-1, j-1] + 1
else
L[i, j] = max { c[i-1, j] , c[i, j-1]}
return c

14. Example
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0
A
B
C
B
D
A
B
for i =1 to m
c[i,0] = 0
for j =0 to n
c[0,j] = 0

15. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0
B 0
C 0
B 0
D 0
A 0
B 0
for i =1 to m
c[i,0] = 0
for j =0 to n
c[0,j] = 0
if xi = yj
then
c[i, j] = c[i-1, j-1]+1
else
L[i, j]=max{c[i-1,j], c[i, j-1]

16. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0
B 0
C 0
B 0
D 0
A 0
B 0
if xi = yj
then
c[i, j] = c[i-1, j-1]+1
else
L[i, j]=max{c[i-1,j], c[i, j-1]

17. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 0+1
B 0
C 0
B 0
D 0
A 0
B 0
if xi = yj
then
c[i, j] = c[i-1, j-1]+1
else
L[i, j]=max{c[i-1,j], c[i, j-1]

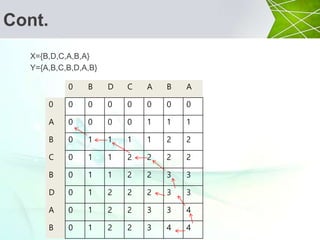
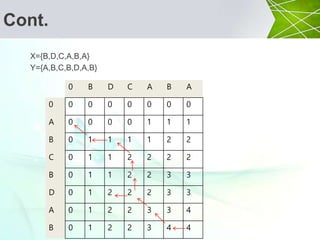
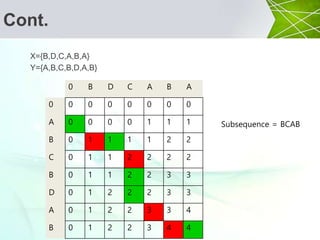
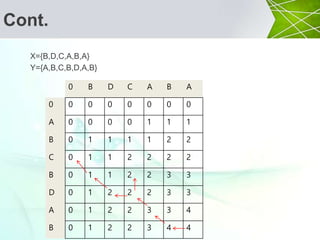
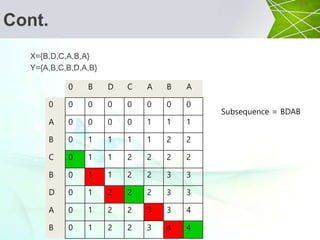
18. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4
if xi = yj
then
c[i, j] = c[i-1, j-1]+1
else
L[i, j]=max{c[i-1,j], c[i, j-1]

19. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4

20. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4

21. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4
Subsequence=BCBA

22. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4

23. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4
Subsequence = BCAB

24. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4

25. Cont.
X={B,D,C,A,B,A}
Y={A,B,C,B,D,A,B}
0 B D C A B A
0 0 0 0 0 0 0 0
A 0 0 0 0 1 1 1
B 0 1 1 1 1 2 2
C 0 1 1 2 2 2 2
B 0 1 1 2 2 3 3
D 0 1 2 2 2 3 3
A 0 1 2 2 3 3 4
B 0 1 2 2 3 4 4
Subsequence = BDAB

26. Cont
We get three longest common subsequences
BCBA
BCAB
BDAB
Length of longest common subsequence is 4

27. Analysis Of LCS
We have two nested loops
– The outer one iterates n times
– The inner one iterates m times
– A constant amount of work is done inside each
iteration of the inner loop
– Thus, the total running time is O(nm)
Space complexity is also O(nm) for n*m table

28. Application
DNA matching
DNA comprises of {A,C,G,T}.
DNA1= AGCCTCAGT
DNA2=ATCCT
DNA3=AGTAGC
DNA 1 and DNA 3 are more similar.
Edit Distance
The Edit Distance is defined as the minimum number of edits neede
d to transform one string into the other.

29. REFERENCES
•Textbook Introduction to Algorithm by Coreman
•http://www.perlmonks.org/?node_id=652798
•https://www.ics.uci.edu/~eppstein/161/960229.html
•https://en.wikipedia.org/wiki/Longest_common_subsequence_probl
em
•http://www.slideshare.net/ShahariarRabby1/longest-common-subse
quence-lcs?qid=49affff4-9c19-4957-bdb9-7877801a569e&v=&b=&fr
om_search=1

30. THANK YOU