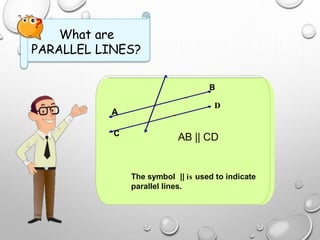
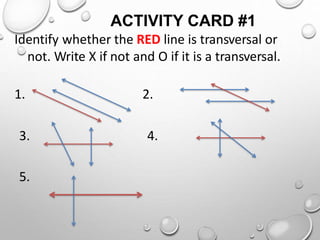
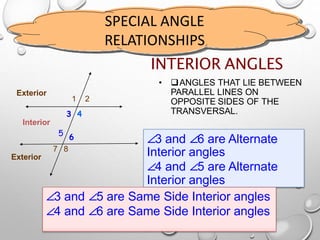
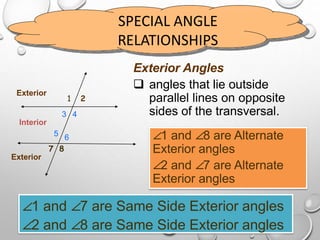
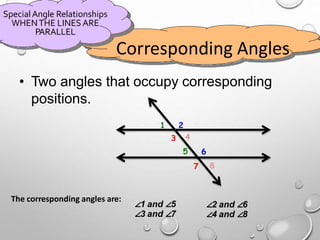
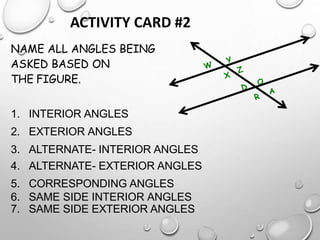
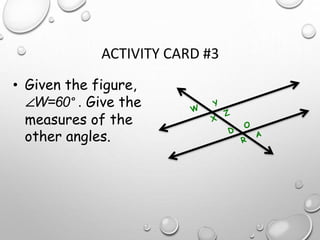
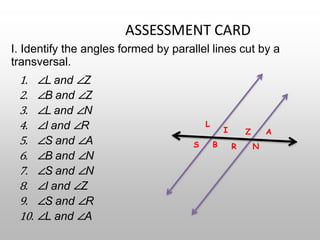
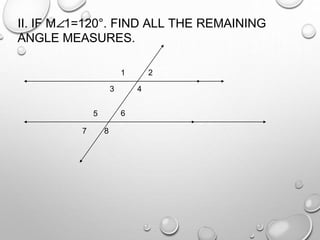
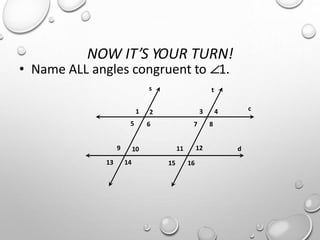
The document discusses parallel lines cut by a transversal and the angle relationships that are formed. It defines parallel lines and transversals, and describes the different types of angles formed, including alternate interior angles, alternate exterior angles, corresponding angles, same side interior angles, and same side exterior angles. Examples are given to demonstrate finding missing angle measures using properties of parallel lines cut by a transversal.

1. Angles formed
by Parallel Lines
cut by a
Transversal

2. GUIDE CARDOBJECTIVES
 Illustrates parallel lines
 Demonstrate knowledge and skills involving
angles formed by parallel lines and
transversal
 Use properties of parallel lines to find
measures of angles, sides and other
quantities involving parallelograms

3. What are
PARALLEL LINES?
PARALLEL LINES are two lines which are
equidistant from each other and do not
meet

4. What are
PARALLEL LINES?
The symbol || is used to indicate
parallel lines.
C
A
AB || CD
B
D

5. What is a
TRANSVERSAL?
A TRANSVERSAL is
line, ray, or segment
that intersects 2 or
more COPLANAR lines,
rays, or segments.
transversal

6. ACTIVITY CARD #1
Identify whether the RED line is transversal or
not. Write X if not and O if it is a transversal.
1. 2.
3. 4.
5.

7. SPECIAL ANGLE
RELATIONSHIPS
INTERIOR ANGLES
• ANGLES THAT LIE BETWEEN
PARALLEL LINES ON
OPPOSITE SIDES OF THE
TRANSVERSAL.
1 2
3 4
65
7 8
Interior
Exterior
Exterior
∠3 and ∠6 are Alternate
Interior angles
∠4 and ∠5 are Alternate
Interior angles
∠3 and ∠5 are Same Side Interior angles
∠4 and ∠6 are Same Side Interior angles

8. SPECIAL ANGLE
RELATIONSHIPS
1 2
3 4
65
7 8
Exterior Angles
 angles that lie outside
parallel lines on opposite
sides of the transversal.
Interior
Exterior
Exterior
∠1 and ∠8 are Alternate
Exterior angles
∠2 and ∠7 are Alternate
Exterior angles
∠1 and ∠7 are Same Side Exterior angles
∠2 and ∠8 are Same Side Exterior angles

9. Corresponding Angles
• Two angles that occupy corresponding
positions.
4
5 6
1 2
3
7 8
∠1 and ∠5
∠3 and ∠7
∠2 and ∠6
∠4 and ∠8
The corresponding angles are:
SpecialAngle Relationships
WHENTHE LINES ARE
PARALLEL

10. Name the pairs of the following angles formed by a
transversal.
Line M
BA
Line N
D E
P
Q
G
F
Line L
Line M
BA
Line N
D E
P
Q
G
F
Line L
Line M
BA
Line N
D E
P
Q
G
F
Line L
500
1300

11. ACTIVITY CARD #2
NAME ALL ANGLES BEING
ASKED BASED ON
THE FIGURE.
1. INTERIOR ANGLES
2. EXTERIOR ANGLES
3. ALTERNATE- INTERIOR ANGLES
4. ALTERNATE- EXTERIOR ANGLES
5. CORRESPONDING ANGLES
6. SAME SIDE INTERIOR ANGLES
7. SAME SIDE EXTERIOR ANGLES

12. Special Angle Relationships
WHEN THE LINES ARE PARALLEL
• ALTERNATE INTERIOR ANGLES
ARE CONGRUENT
• ALTERNATE EXTERIOR ANGLES
ARE CONGRUENT
• SAME SIDE INTERIOR ANGLES ARE
SUPPLEMENTARY
• SAME SIDE EXTERIOR ANGLES
ARE SUPPLEMENTARY
1 2
3 4
Interior
5 6
7 8
If the lines are not
parallel, these angle
relationships DO NOT
EXIST.
Exterior
Exterior

13. LET’S PRACTICE
M<1=120°
FIND ALL THE REMAINING
ANGLE MEASURES.
1
4
2
65
7 8
3
60°
60°
60°
60°
120°
120°
120°
120°

14. TRY IT
OUT
x + 102x + 20
What do you know about the angles?
Write the equation.
Solve for x.
SUPPLEMENTARY
2x + 20 + x + 10 = 180
3x + 30 = 180
3x = 150
x = 50

15. 2x - 60
3x - 120
What do you know about the angles?
Write the equation.
Solve for x.
ALTERNATE INTERIOR
3x - 120 = 2x - 60
x = 60
Subtract 2x from both sides
Add 120 to both sides

16. ANOTHER PRACTICE PROBLEM
FIND ALL THE
MISSING ANGLE
MEASURES
40°
120°
120°
60°
60°
40°
60°
60°
180-(40+60)= 80°
80°
80°
80°
100°
100°
12
3
4
5
6 7
8
11
10
9
12

17. ACTIVITY CARD #3
• Given the figure,
∠W=60° . Give the
measures of the
other angles.

18. ASSESSMENT CARD
I. Identify the angles formed by parallel lines cut by a
transversal.
1. ∠L and ∠Z
2. ∠B and ∠Z
3. ∠L and ∠N
4. ∠I and ∠R
5. ∠S and ∠A
6. ∠B and ∠N
7. ∠S and ∠N
8. ∠I and ∠Z
9. ∠S and ∠R
10. ∠L and ∠A
L
I Z A
S B R N

19. II. IF M∠1=120°. FIND ALL THE REMAINING
ANGLE MEASURES.
1
4
2
65
7 8
3

20. Parallel Lines w/a transversal and
Angle Pair Relationships
Concept
Summary
Congruent Supplementary
alternate interior angles- AIA
alternate exterior angles- AEA
corresponding angles - CA
vertical angles- VA
same side interior angles- SSI
same side exterior angles- SSE
Types of angle pairs formed when
a transversal cuts two parallel lines.
linear pair of angles- LP

21. NOW IT’S YOUR TURN!
• Name ALL angles congruent to ∠1.
s t
c
d
1 2
6
3 4
5 7 8
9 10 11 12
13 14 15 16

22. REFERENCE CARD
• Learner’s Material – Mathematics VIII, First Edition
2013 pp. 482- 487
•http://daniellmiddle.typepad.com/files/angle-measures-parallel-
lines-cut-by-a-transversal-ppt--tmi-lsn-6.01-ppt.ppt
•http://www.lcboe.net/userfiles/233/Classes/645/Similar%20Tria
ngle%20Criteria.ppt
• http://www.mathnstuff.com/math/spoken/here/2cla
ss/260/trans.htm

23. ANSWER CARD
Activity Card #1
1.
2.
3.
4.
5.
X
O
O
O
X
Activity Card #2
1.
2.
3.
4.
5.
∠X, ∠Z, ∠D, ∠O
∠W, ∠Y, ∠R, ∠A
∠X and ∠O; ∠Z and ∠D
∠W and ∠A; ∠Y and ∠R
∠Wand ∠D; ∠X and ∠R; ∠Y and ∠O; ∠Z
and ∠A
∠X and ∠D; ∠Z and ∠O6.
∠W and ∠R; ∠Y and ∠A
Activity Card #3
1.
2.
3.
m∠Y=120°
m∠X=120°
m∠Z=60°
4. m∠D=60°
5.
6.
7.
m∠0=120°
m∠R=60°
m∠A=120°
ASSESSMENT CARD
I.
1.corresponding angles
2. Alternate interior angles
3. Alternate exterior angles
4. Alternate interior angles
5. Alternate exterior angles
6. Corresponding angles
7. Same side exterior angle
8. Same side interior angle
9. Corresponding angles
10.Same side exterior angle II.
m∠2=60°
m∠3=60°
m∠4=120°
m∠5=120°
m∠6=60°
m∠7=60°
ms∠8=120°
NOW IT’S YOUR TURN!
∠6; ∠3; ∠8; ∠9; ∠14; ∠11; ∠16