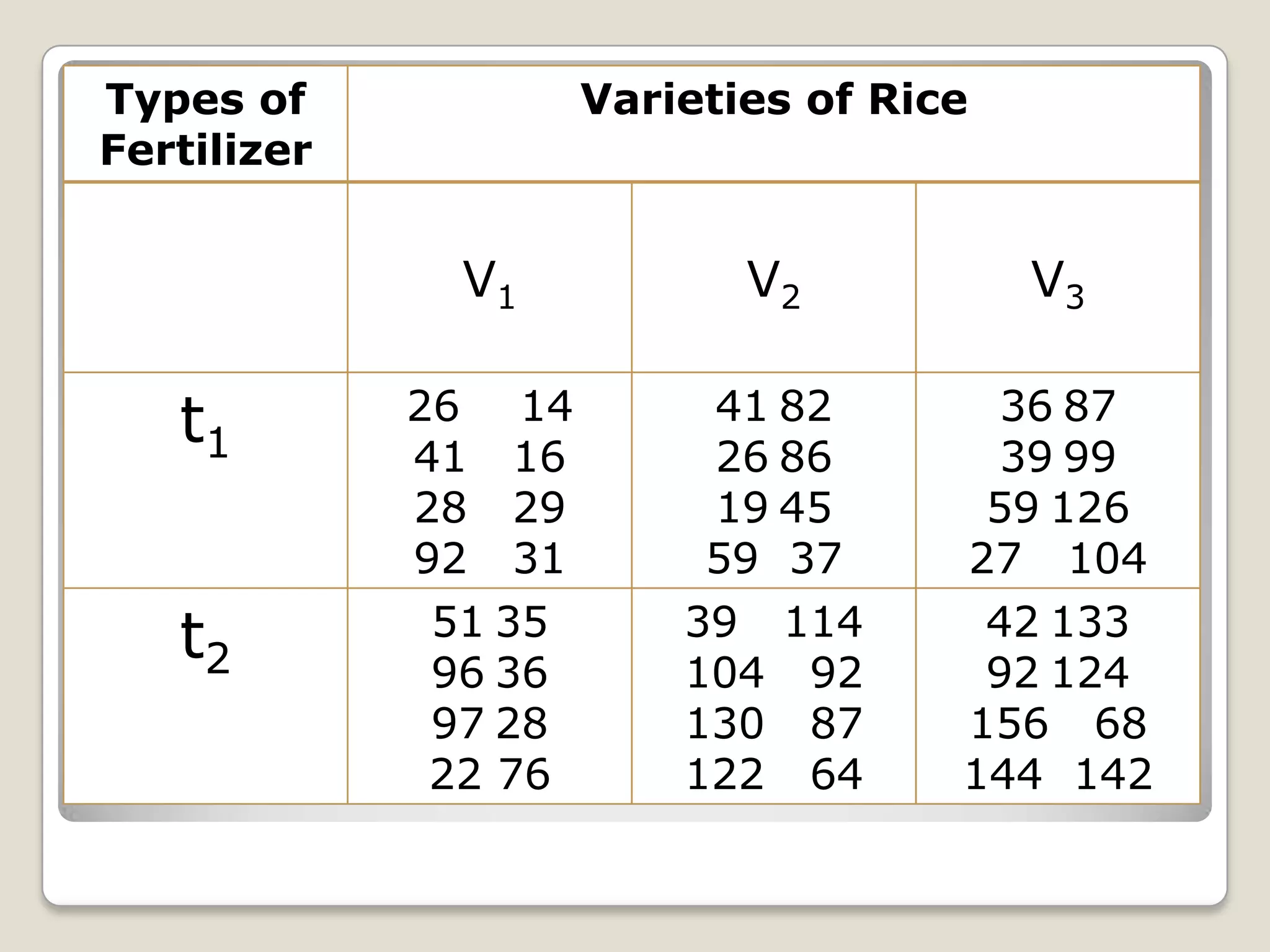
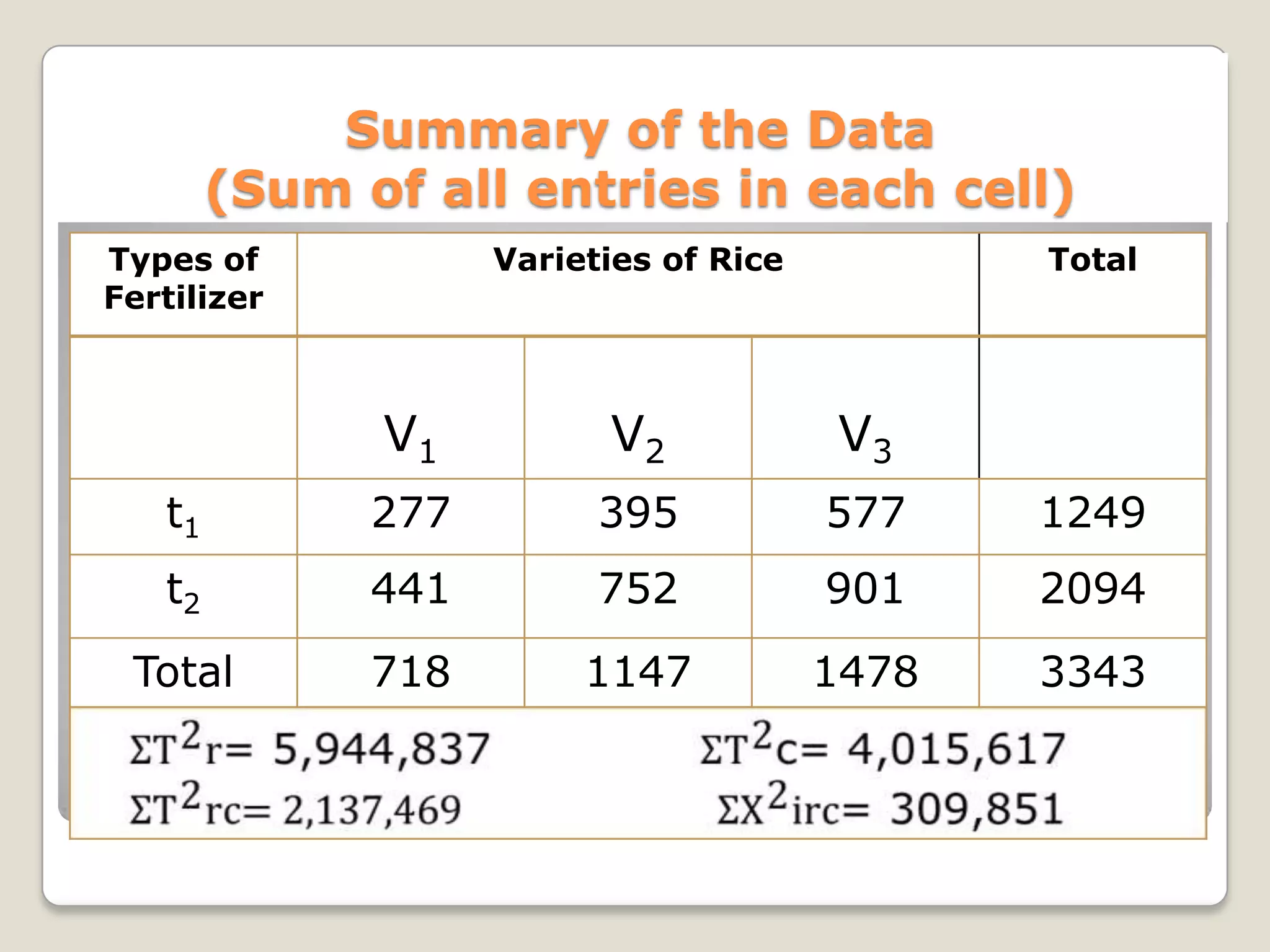
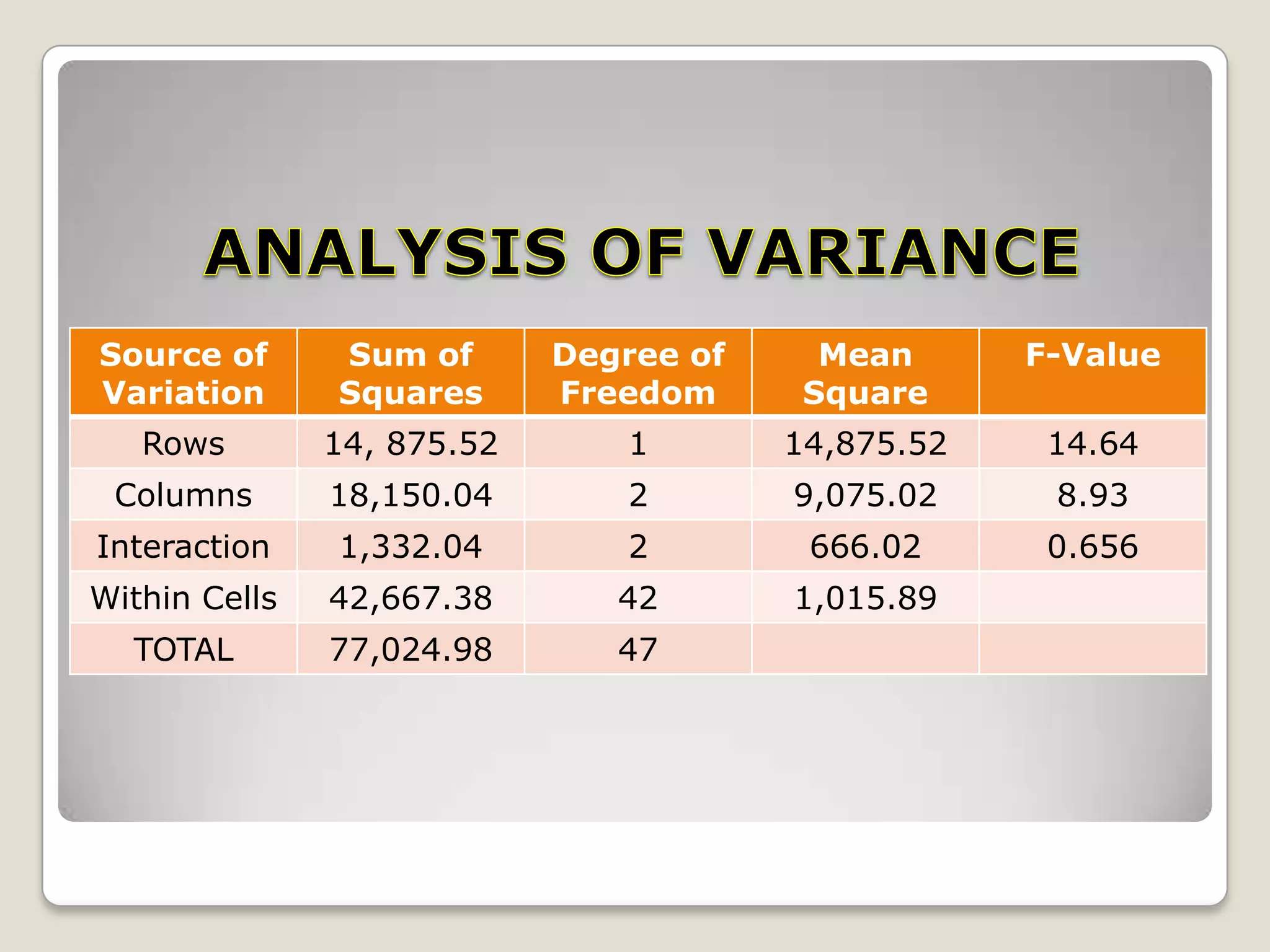
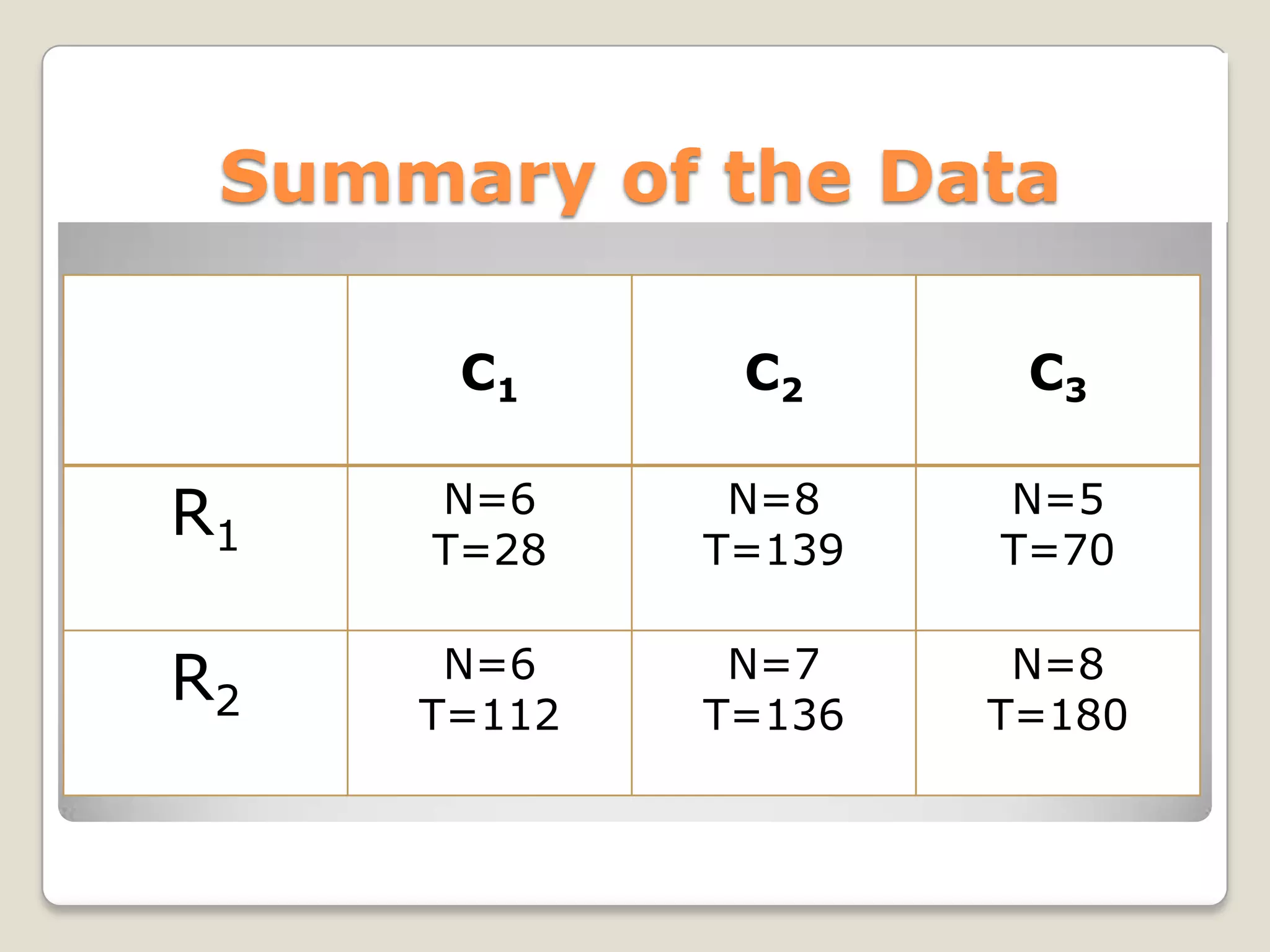
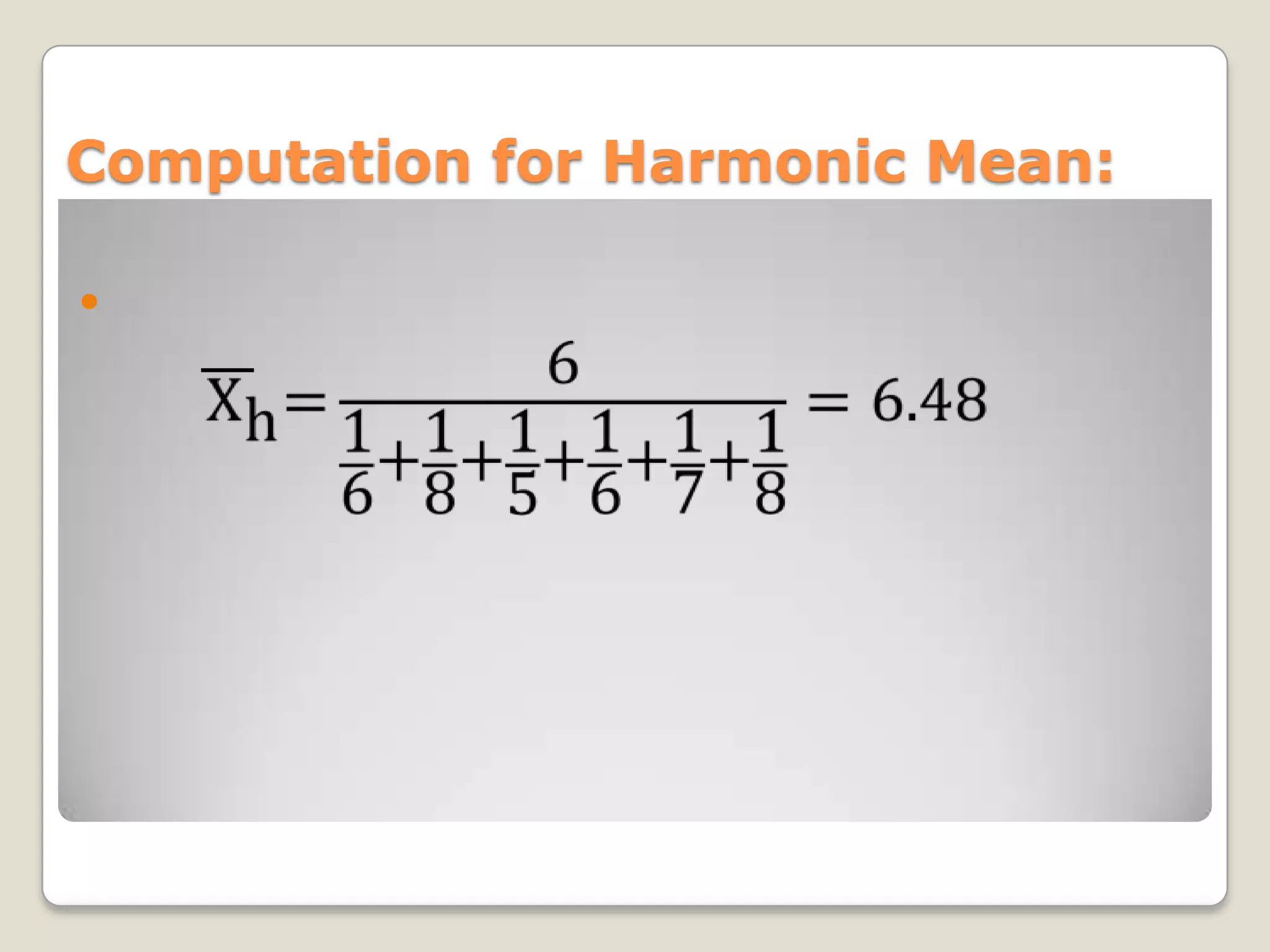
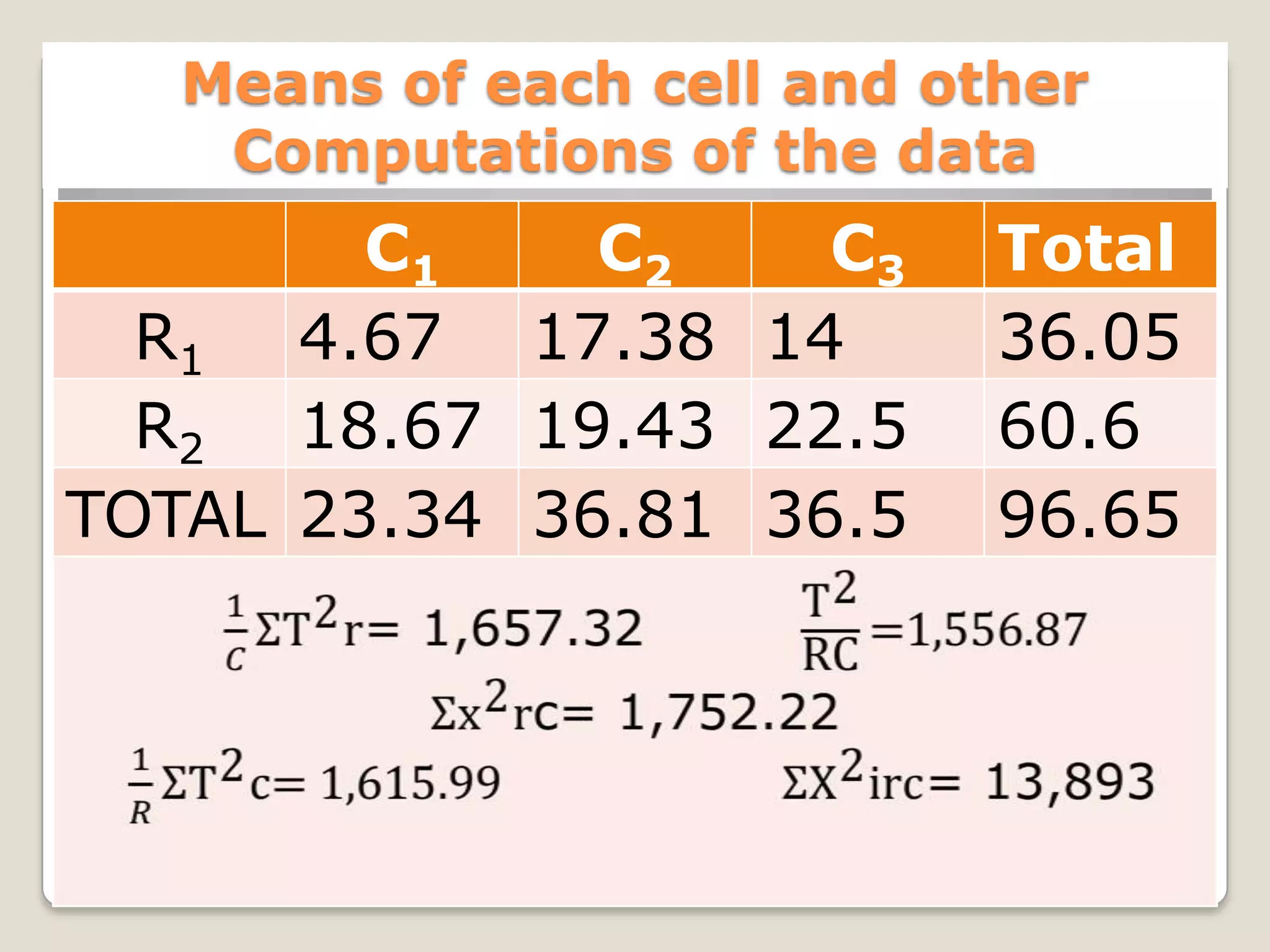
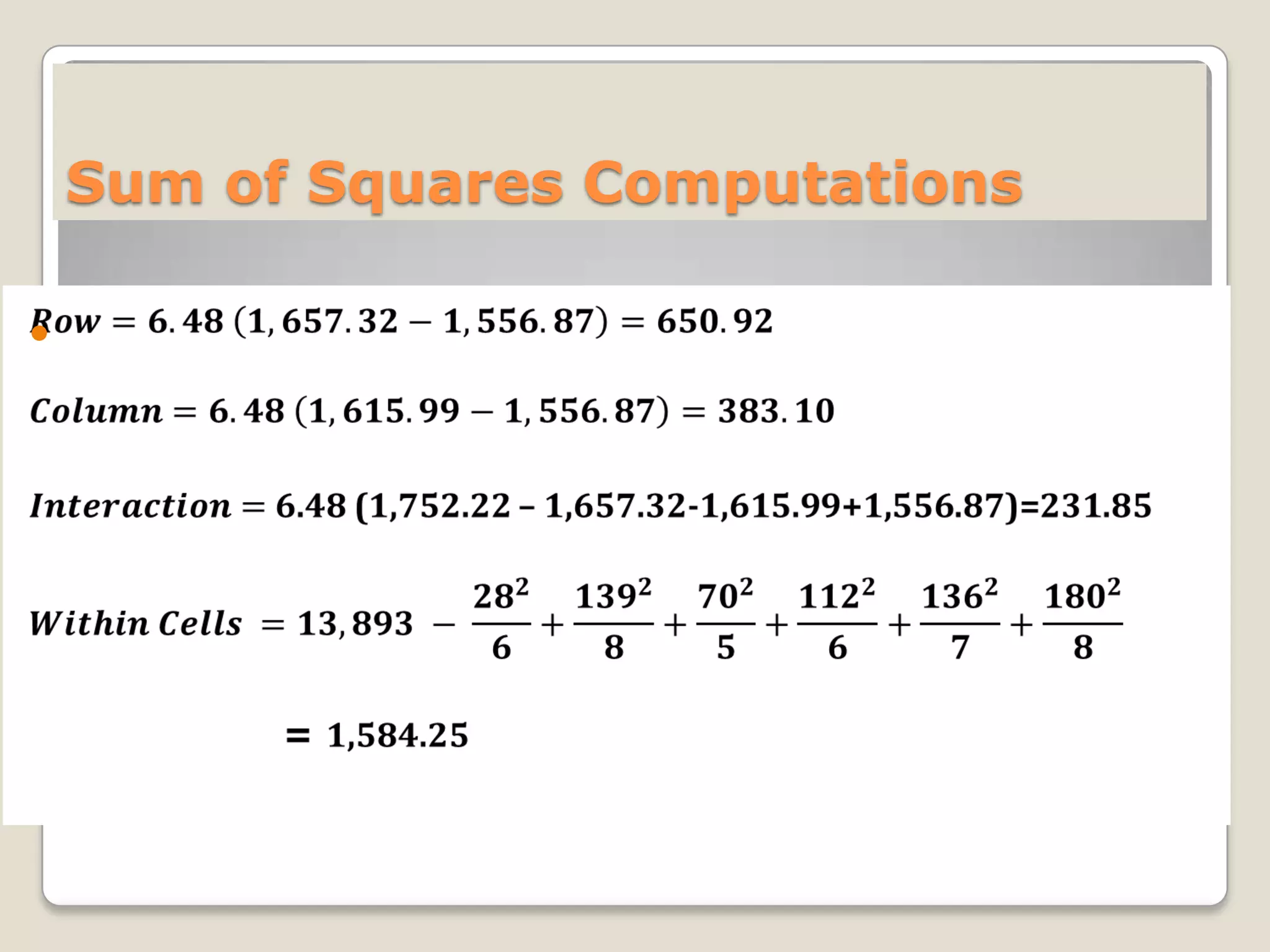
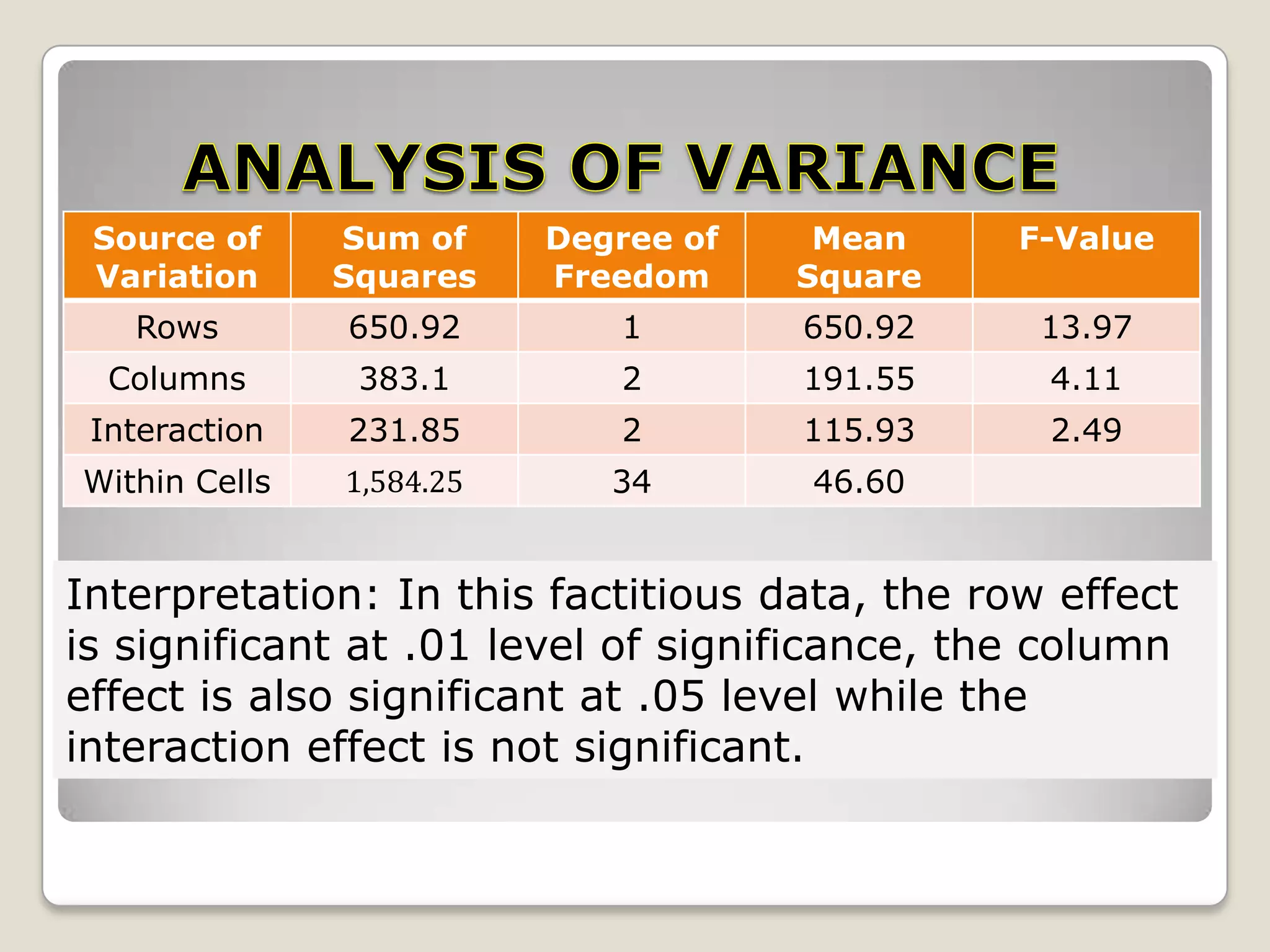
This document describes the two-way analysis of variance (ANOVA) test, which analyzes the effects of two independent variables on a continuous dependent variable. It provides formulas and an example to illustrate how to calculate the sum of squares, degrees of freedom, mean squares, and F-values for the row factor, column factor, interaction between rows and columns, and residual error. The example analyzes the yield of three rice varieties under two fertilizer types. The results show that both the variety and fertilizer type significantly affect yield, but there is no significant interaction between the two factors. The document also describes how to perform two-way ANOVA when cell frequencies are unequal by adjusting calculations using harmonic means.

1. ANALYSIS OF
VARIANCE
(F-RATIO TEST)
TWO WAY
CLASSIFICATION

2. This test is designed for more than
two groups of objects studies to see if
each group is affected by two different
experimental conditions.

3. This test is used when the
number of observation in the
subclasses are equal.

4. Formulas for Two Way ANOVA
For Equal and Proportionate Entries in the
Subclasses
Source of
Variation
Sum of Squares
Degrees
of
Freedom
Row
R–1
Column
C–1
Interaction
(R–1)(C–1)
Within cells
RC (n-1)
Total
nRC – 1
Mean
Square
Fvalue

5. 

6. Example
An agricultural experiment was
conducted to compare the yields of
three varieties of rice applied by
two
types
of
fertilizer.
The
following table represents the yield
in grams using eight plots.

7. Types of
Fertilizer
Varieties of Rice
V1
t1
t2
V2
V3
26 14
41 16
28 29
92 31
51 35
96 36
97 28
22 76
41 82
26 86
19 45
59 37
39 114
104 92
130 87
122 64
36 87
39 99
59 126
27 104
42 133
92 124
156 68
144 142

8. Hypothesis
There is no difference in the yields of the
three varieties of rice.
2. The two types of fertilizer does not
significantly affect the yields meaning
the yield is not dependent of the type of
fertilizer used.
3. There is no significant interaction
between the variety of rice and the types
of fertilizer used.
1.

9. Summary of the Data
(Sum of all entries in each cell)
Types of
Fertilizer
Varieties of Rice
Total
V1
V2
V3
t1
277
395
577
1249
t2
441
752
901
2094
Total
718
1147
1478
3343

10. Sum of Squares Computations


11. Source of
Variation
Sum of
Squares
Degree of
Freedom
Mean
Square
F-Value
Rows
14, 875.52
1
14,875.52
14.64
Columns
18,150.04
2
9,075.02
8.93
Interaction
1,332.04
2
666.02
0.656
Within Cells
42,667.38
42
1,015.89
TOTAL
77,024.98
47

12. Interpretations
1. For the different varieties of rice, we have Fc=8.93 with 2 df
associated with the numerator and 42 df with the denominator.
The values required for significance at 5% and 1% levels are 3.22
and 5.15, respectively. We conclude that the different varieties of
rice differ significantly in their yields.
2. For the different types of fertilizer, we have Fr=14.64 with 1 df
associated with the numerator and 42 df with the denominator.
The value required for the significance at 5% and 1% levels are
4.072 & 7.287 respectively. We conclude therefore that the
different types of fertilizer affect significantly the yields of rice.
3. For significant interaction, we have Frc=0.656 which is lower
than the table value. Therefore hypothesis number three is
accepted.

13. This method is applied in two way
ANOVA where the number of observations in
the subclasses or cell frequency is unequal.
The data is to be adjusted by the method of
unweight mean. This method is in effect the
analysis of variance applied to the means of
the subclasses. The sum of the squares for
rows, columns, and interaction are then
adjusted using the harmonic mean.

14. 

15. Formulas for Two Way ANOVA
For Unequal Frequency in the Subclasses
Source of
Variation
Sum of Squares
Degrees
of
Freedom
Row
R–1
Column
C–1
Interaction
(R–1)(C–1)
Within cells
N-RC
Mean
Square
Fvalue

16. Example
The following table shows of
factitious data for a two way
classification experiment with two
levels of one factor and three
levels of the other factor.

17. C1
R1
R2
7 6
6 2
4 3
23 22
14 26
9
18
C2
8
12
16
24
17
19
21
22
11 26
15 14
26 13
31
C3
16
17
10
9
27
31
42
13
14
16
17
18
20

18. Summary of the Data
C1
C2
C3
R1
N=6
T=28
N=8
T=139
N=5
T=70
R2
N=6
T=112
N=7
T=136
N=8
T=180

19. Computation for Harmonic Mean:


20. Means of each cell and other
Computations of the data
C1
C2
C3
R1 4.67 17.38 14
R2 18.67 19.43 22.5
TOTAL 23.34 36.81 36.5
Total
36.05
60.6
96.65

21. Sum of Squares Computations


22. Source of
Variation
Sum of
Squares
Degree of
Freedom
Mean
Square
F-Value
Rows
650.92
1
650.92
13.97
Columns
383.1
2
191.55
4.11
Interaction
231.85
2
115.93
2.49
Within Cells
1,584.25
34
46.60
Interpretation: In this factitious data, the row effect
is significant at .01 level of significance, the column
effect is also significant at .05 level while the
interaction effect is not significant.

23. THANK YOU 