1. การวัดการกระจายของข้อมูล
Range (พิสัย)
Quartile deviation (ส่วนเบี่ยงเบนควอไทล์)
Mean deviation (ส่วนเบี่ยงเบนเฉลี่ย)
Standard deviation (ส่วนเบี่ยงเบนมาตรฐาน)

2. Range (พิสัย)
ตัวอย่าง อายุนักเรียนกลุ่มหนึ่งคือ
18 14 22 15 16 17 21 23 19 20
Range = minmax xx 
1423
9
ตัวอย่าง อายุนักเรียนกลุ่มหนึ่งคือ
18 14 22 15 16 17 21 23 19
20 15 17 17 19 20 21 22 18

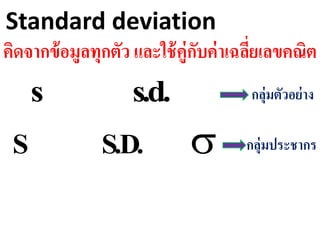
3. ข้อมูลแบบแจกแจงความถี่
น้าหนักของพนักงาน 70 คน (หน้า 189)
589.
น้ำหนัก จำนวนพนักงำน
60 – 64 4
65 – 69 10
70 – 74 16
75 – 79 15
80 – 84 14
85 - 89 11
Range = ขอบบนชั้นสูงสุด -ขอบล่างชั้นต่าสุด
Range = 559.
30
พิสัยของน้าหนักพนักงาน= 30 ก.ก.

4. Standard deviation
คิดจากข้อมูลทุกตัว และใช้คู่กับค่าเฉลี่ยเลขคณิต
.d.ss
.D.SS
กลุ่มตัวอย่าง
กลุ่มประชากร

5. Standard deviation
n
)xx(
s
n
i
i 
 1
2
21
2
)x(n
)x(
s
n
i
i


 

6. ตัวอย่าง (หน้า 206) คะแนนของนักเรียน 5 คน
23 28 32 30 37
n
x
x
n
i
i
 1
5
5
1

 i
i
x
5
3730322823 

305
150


7. ตัวอย่าง (หน้า 191) คะแนนของนักเรียน 5 คน
23 28 32 30 37
21
2
)x(n
x
s
n
i
i


 
2
22222
305
3730322823
)(
)()()()()(
s 


30
9005
4606
s 9002921  .
221.s  64.

8. Standard deviation ข้อมูลแจกแจงความถี่
n
)xx(f
s
k
i
ii 
 1
2
21
2
)x(n
)x(f
s
k
i
ii


 
n
xf
x
k
i
ii
 1

9. ข้อมูลแบบแจกแจงความถี่
คะแนนสอบ จำนวนคน
21 - 25 4
26 - 30 6
31 - 35 10
36 - 40 6
41 - 45 4
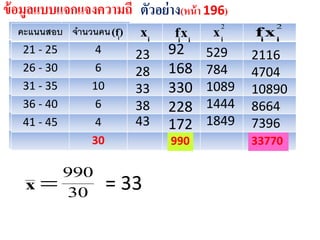
ตัวอย่าง(หน้า 196)
คะแนนสอบ จำนวนคน
21 - 25 4
26 - 30 6
31 - 35 10
36 - 40 6
41 - 45 4
30
30
990
x
)f( i ix
23
28
33
38
43
iixf
92
168
330
228
172
2
ix
529
784
1089
1444
1849
2
iixf
2116
4704
10890
8664
7396
990 33770
= 33

10. ข้อมูลแบบแจกแจงความถี่
คะแนนสอบ จำนวนคน
21 - 25 4
26 - 30 6
31 - 35 10
36 - 40 6
41 - 45 4
ตัวอย่าง(หน้า 195)
คะแนนสอบ จำนวนคน
21 - 25 4
26 - 30 6
31 - 35 10
36 - 40 6
41 - 45 4
30
)f( i ix
23
28
33
38
43
iixf
23
28
33
38
43
2
ix
529
784
1089
1444
1849
2
iixf
2116
4704
10890
8664
7396
990 33770
33x
2
3330
33770
)(21
2
)x(n
)x(f
s
k
i
ii


  S = 6.06

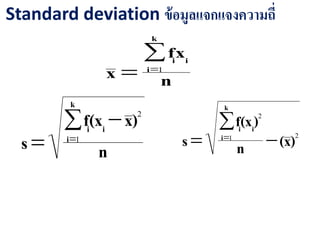
11. Note Standard deviation
1. ถ้าข้อมูลเท่ากันทุกตัว s.d. =0
2. ถ้านาค่าคงที่ไปบวกหรือลบออกจากข้อมูลทุกตัว
s.d. เท่าเดิม
3. ถ้านาค่าคงที่ไปคูณหรือหารออกจากข้อมูลทุกตัว
s.d. = s.d.เดิม คูณหรือหารด้วยค่าสมบูรณ์ค่าคงที่นั้น
4. s.d. มีค่าเท่ากับหรือมากกว่า 0
และมีหน่วยเดียวกับข้อมูล

12. Variance (ความแปรปรวน)
ส่วนเบี่ยงเบนมาตรฐานยกกาลังสอง
n
)xx(f
s
k
i
ii 
 1
2
21
2
)x(n
)x(f
s
k
i
ii


 
n
)xx(f
s
k
i
ii 
 1
2
2
21
2
2
)x(n
)x(f
s
k
i
ii


 

13. การวัดการกระจายสัมพัทธ์
เพื่อเปรียบเทียบกำรกระจำยของข้อมูล
ตั้งแต่ 2 ชุดขึ้นไป
อยู่รูปของ %

14. ตัวอย่าง(206) เปรียบเทียบรายได้ของ 2 หมู่บ้าน
รำยได้ของบ้ำนแมตซิตี้จำนวน 5 ครอบครัวคือ
6,400 3,500 4,200 2,400 5,100
รำยได้ของบ้ำนอุ่มเม้ำซิตี้จำนวน 7 ครอบครัว คือ
2,100 1,750 3,080 3,200 2,000 2,600 2,300
สัมประสิทธิ์พิสัย = 100

minmax
minmax
XX
XX
สัมประสิทธิ์พิสัยครอบครัวของบ้ำนแมตซิตี้ = 10040024006
40024006


,,
,,
%.4545

15. สัมประสิทธิ์พิสัยครอบครัวของบ้ำนอุ่มเม้ำซิตี้ = 10075012003
75012003


,,
,,
%.2929
สัมประสิทธิ์พิสัยของบ้ำนแมตซิตี้ > สัมประสิทธิ์พิสัยของบ้ำนอุ่มเม้ำซิตี้
รำยได้ของครอบครัวของบ้ำนแมตซิตี้ มีควำมแตกต่ำงกันมำกกว่ำรำยได้
ครอบครัวของบ้ำนอุ่มเม้ำซิตี้

16. ตัวอย่าง(208) เปรียบเทียบราคาสิ้นค้า 2 ชนิด
สัมประสิทธิ์กำรแปรผัน = 100x
s
66.
รำคำสินค้ำชนิดที่ 1 (บำท) 3 6 5 7 12
รำคำสินค้ำชนิดที่ 2 (บำท) 45 52 60 39 44
5
127563
1

x
013.5
6612667665666663 22222
1
).().().().().(
s


สัมประสิทธิ์กำรแปรผัน
สินค้ำชนิดที่ 1 10066
013
 .
.
%.6145

17. 485
4439605245
2

x
297.5
48444839486048524845 22222
1
)()()()()(
s


สัมประสิทธิ์กำรแปรผัน
สินค้ำชนิดที่ 2 10048
297

.
%.1915
สัมประสิทธิ์กำรแปรผันรำคำสินค้ำชนิดที่ 1
มำกกว่ำสัมประสิทธิ์กำรแปรผันสินค้ำชนิดที่ 2
สินค้ำชนิดที่ 1 มีกำรกระจำยมำกกว่ำชนิดที่ 2
นั่นคือ สินค้ำชนิดที่ 1 มีกำรขึ้นลงของรำคำมำกกว่ำสินค้ำชนิดที่ 2

18. สอบ
หน้า 214-216 ข้อ 1-10
ส่งไม่เกินวันพรุ่งนี้ เวลา 13.00 น.