1. 13
สถิติเพื่องานอาชีพ

2. การสุ่มตัวอย่าง(Sampling)
กระบวนการได้มาซึ่งกลุ่มตัวอย่าง
ที่เป็นตัวแทนที่ดีของประชากร
เพื่อการศึกษาข้อมูลแทนประชากร

3. ความหมายของคาที่เกี่ยวข้องการสุ่มตัวอย่าง
-Population(ประชากร)
1. Finite Population(ประชากรแบบจากัด)
2. Infinite Population(ประชากรไม่จากัดหรืออนันต์)
-Sample(กลุ่มตัวอย่าง)
-Sampling(การสุ่มตัวอย่าง)
1. ลดค่าใช้จ่าย
2. ประหยัดเวลา
3. ลดจานวนบุคลากรในการเก็บข้อมูล

4. ประเภทการสุ่มตัวอย่าง
การสุ่มตัวอย่างโดยใช้ความน่าจะเป็น
1. การสุ่มตัวอย่างแบบง่าย
(Simple Random Sampling)
- จับฉลาก
- ตารางเลขสุ่ม

5. - ตารางเลขสุ่ม
862 245 458 396 522 498 298 665 635 665 113 917
223 398 183 765 138 369 163 743 593 252 581 355
749 824 721 967 287 556 628 843 725 731 553 253
522 967 259 532 618 624 396 562 134 563 932 441

6. 2. การสุ่มตัวอย่างแบบมีระบบ
(Systematic Random Sampling)
มีรายชื่อเรียงอยู่ในระบบแล้ว
ทุกๆ 5 คน เลือก 1 คน
คนทั้งหมด 40 คน ต้องการตัวอย่าง 8 คน
8
40
n
N
ข้อดี คือ เสียค่าใช้จ่ายต่า สะดวกและรวดเร็ว

7. 3. การสุ่มตัวอย่างแบบเป็นกลุ่ม
(Cluster Random Sampling)
แต่ละกลุ่มมีลักษณะที่เหมือนกัน
นศ.ชย. 1 มี 8 กลุ่ม แต่ละกลุ่มมีลักษณะที่เหมือนกัน
เลือกมาเป็นตัวแทน 3 กลุ่ม
ข้อดี คือ เสียค่าใช้จ่ายต่า สะดวกและรวดเร็ว

8. 4. การสุ่มตัวอย่างแบบชั้นภูมิ
(Stratified Random Sampling)
แบ่งประชากรออกเป็นระดับหรือชั้นภูมิ แต่ละระดับเหมือนกัน
ระดับ ปวช. 1
ระดับ ปวช. 2
ระดับ ปวช. 3
ระดับ ปวส. 1
ระดับ ปวส. 2
ข้อดี คือ ได้ตัวแทนที่ดี ข้อเสีย คือ ค่าใช้จ่ายสูง

9. 5. การสุ่มตัวอย่างแบบหลายขั้นตอน
(Multi-Stage Random Sampling)
ประชากรกลุ่มเดียวกันแตกต่างกัน ประชากรต่างกลุ่มเหมือนกัน
ภาค
ข้อดี คือ ได้ตัวแทนที่ดี ข้อเสีย คือ ค่าใช้จ่ายสูง
อาเภอจังหวัด ตาบล
หมู่บ้าน

10. การสุ่มตัวอย่างโดยไม่ใช้ความน่าจะเป็น
(No Probability Sampling)
ไม่คานึงว่าแต่ละหน่วยมีโอกาสที่จะถูกเลือกมากน้อยเพียงไร
บางครั้งไม่ต้องอ้างอิงถึงกลุ่มประชากร
ข้อดี คือ สะดวด ประหยัด

11. การสุ่มตัวอย่างโดยไม่ใช้ความน่าจะเป็น
(No Probability Sampling)
1. การสุ่มตัวอย่างแบบบังเอิญ
(Accident Sampling)
สอบถามคนที่มาเที่ยวงานวัน Open House

12. 2. การสุ่มตัวอย่างแบบโควตา
(Quota Sampling)
สอบถามคนที่มาเที่ยวงานวัน Open House
แต่ถามนักเรียนมัธยม 30 คน คนทั่วไป 20 คน

13. ขนาดของตัวอย่าง(Sample Size)
มากพอที่จะเป็นตัวแทนของประชากรได้
Taro Yamane
2
1 Nd
N
n 
n = ขนาดของตัวอย่าง
N = ประชากร
d = ระดับนัยความมีนัยสาคัญ

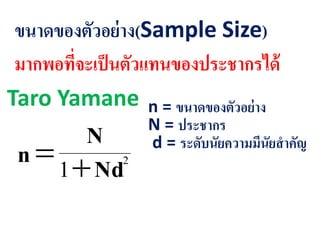
14. ตัวอย่าง ประชากร 500 คน ต้องการความมีนัยสาคัญทาง
สถิติ .05 (ยอมรับให้เกิดความผิดพลาด 5 %)
2
1 Nd
N
n 
2
055001
500
))(.(n 
22222.n
กลุ่มตัวอย่าง คือ 223 คน