Recommended
PPT
PPT
สถิติพรรณนาในการวิจัยเชิงปริมาณ ปรับSlide-เพิ่มslideงานมอบหมาย
PPT
PPT
การวิเคราะห์ข้อมูลเชิงปริมาณ
DOCX
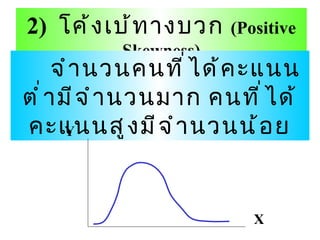
PPT
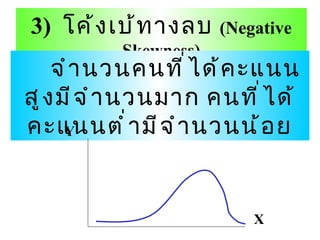
วิธีการสำคัญในการวิเคราะห์ข้อมูลเชิงปริมาณ
PPT
สัปดาห์ที่ 7 8 (2 dec 2010)
PPTX
PPTX
PDF
PDF
83 สถิติและการวิเคราะห์ข้อมูล ตอนที่10_คะแนนมาตรฐาน
PDF
PDF
PDF
PDF
82 สถิติและการวิเคราะห์ข้อมูล ตอนที่9_การกระจายสัมพัทธ์
PPT
ความรู้เบื้องต้นเกี่ยวกับสถิติ อภิเทพ
PDF
PDF
วิธีการสุ่มตัวอย่างและการเก็บรวบรวมข้อมูล
PPTX
PPT
PDF
Stat 101 Module2 การวิเคราะห์และแปลผล
PDF
77 สถิติและการวิเคราะห์ข้อมูล ตอนที่4_แนวโน้มเข้าสู่ส่วนกลาง3
PDF
PDF
Big Data 101 : Chapter 8 Module 1
PPT
PPTX
1 เขียนโปรแกรมภาษา C# "คำนวณคะแนนเฉลี่ย"
PPTX
2. เขียนโปรแกรม C# "ตัดเกรด"
PPTX
PDF
การวิเคราะห์ข้อสอบด้วยโปรแกรม Evana
PPTX
การสังเคราะห์งานวิจัยด้วย การวิเคราะห์อภิมาน
More Related Content
PPT
PPT
สถิติพรรณนาในการวิจัยเชิงปริมาณ ปรับSlide-เพิ่มslideงานมอบหมาย
PPT
PPT
การวิเคราะห์ข้อมูลเชิงปริมาณ
DOCX
PPT
วิธีการสำคัญในการวิเคราะห์ข้อมูลเชิงปริมาณ
PPT
สัปดาห์ที่ 7 8 (2 dec 2010)
PPTX
What's hot
PPTX
PDF
PDF
83 สถิติและการวิเคราะห์ข้อมูล ตอนที่10_คะแนนมาตรฐาน
PDF
PDF
PDF
PDF
82 สถิติและการวิเคราะห์ข้อมูล ตอนที่9_การกระจายสัมพัทธ์
PPT
ความรู้เบื้องต้นเกี่ยวกับสถิติ อภิเทพ
PDF
PDF
วิธีการสุ่มตัวอย่างและการเก็บรวบรวมข้อมูล
PPTX
PPT
PDF
Stat 101 Module2 การวิเคราะห์และแปลผล
PDF
77 สถิติและการวิเคราะห์ข้อมูล ตอนที่4_แนวโน้มเข้าสู่ส่วนกลาง3
PDF
PDF
Big Data 101 : Chapter 8 Module 1
PPT
Viewers also liked
PPTX
1 เขียนโปรแกรมภาษา C# "คำนวณคะแนนเฉลี่ย"
PPTX
2. เขียนโปรแกรม C# "ตัดเกรด"
PPTX
PDF
การวิเคราะห์ข้อสอบด้วยโปรแกรม Evana
PPTX
การสังเคราะห์งานวิจัยด้วย การวิเคราะห์อภิมาน
PDF
DOC
PDF
PDF
PDF
Slใบเก็บคะแนนระหว่างเรียนรายวิชาวิทยาศาสตร์ ว 23101 2 ชั้นมัธยมศึกษาปีที่ 3
PDF
DOC
DOC
การวัดตำแหน่งที่และการกระจาย
PDF
PDF
การวัดตำแหน่งที่ของข้อมูลม.6
PDF
PDF
ข้อสอบคอมพิวเตอร์ PowerPoint +internet
Similar to สถิติเชิงบรรยาย
PPT
PDF
Introduction to Statistics: Descriptive Statistics
PDF
%Ca%c3%d8%bb%ca%b6%d4%b5%d4%5 b1%5d
PDF
DOC
PPT
PDF
descriptive.pdfการวิเคราะห์ข้อมมูลสำหรับการศึกษา
PPTX
17 การวัดการกระจายของข้อมูล
PPTX
17 การวัดการกระจายของข้อมูล
PPTX
Spc basic for training in thai
PPTX
เอกสารบรรยาย เรื่อง แนวทางการใช้สถิติเพื่อการวิจัยทางการศึกษาและการใช้คอมพิวเ...
PDF
PPT
Week 5 scale_and_measurement
PDF
Chapter5 descriptive statistic
PPT
Week 8 conceptual_framework
PDF
PDF
PDF
DOC
เอกสารประกอบการสอนบทที่ 1
PPTX
สถิติเชิงบรรยาย 1. 2. 9.1 การแจกแจงความถี่ การแจกแจง ( Distribution) หมายถึง ลักษณะที่ ตัวแปรตัวหนึ่งจะมีค่าต่างๆ ในขอบเขตของค่าที่เป็นไปได้ ความถี่ ( Frequency) หมายถึง จำนวนรายการ ข้อมูลหรือจำนวนคะแนนที่ซ้ำกัน การแจกแจงความถี่ ( Frequency distribution) หมายถึง การแจกแจงจำนวนรายการข้อมูลหรือคะแนนที่ซ้ำกันที่ตกอยู่ในช่วงคะแนนที่กำหนดไว้ 3. การสร้างตารางแจกแจงความถี่ 1) การแจกแจงความถี่ของข้อมูลแบบ จัดกลุ่ม / ไม่ต่อเนื่อง ( Categorical data) 2) การแจกแจงความถี่ของข้อมูลแบบต่อเนื่อง - แจกแจงแบบไม่ต้องจัดเป็นกลุ่ม เป็นการเรียงลำดับคะแนน - แจกแจงแบบจัดเป็นกลุ่ม 4. ขั้นตอนการสร้างตารางแจกแจงความถี่ 1) หาข้อมูลที่มีค่าสูงสุดและต่ำสุด 2) หาผลต่างระหว่างข้อมูลค่าสูงสุดกับต่ำสุด ( พิสัย ) 3) กำหนดจำนวนชั้น นิยมกำหนดระหว่าง 5-20 ชั้น 4) คำนวณหาขนาดความห่างของข้อมูลแต่ละชั้นหรืออันตรภาค ( Interval) จากสูตร i = (U – L) / N 5. 6. 1) โค้งปกติ ( Normal Curve จำนวนคนที่ได้คะแนนสูงและต่ำมีจำนวนน้อย คะแนนปานกลางมีจำนวนมากที่สุด ถ้าลากเส้นตรงจากจุดยอดโค้งมาตั้งฉากกับฐานแล้วพับตามรอยประ ส่วนโค้งจะทับกันสนิท Y X 7. เป็นรูประฆังคว่ำ ( bell shaped) มียอดเดียว สมมาตร Mean = Mode = median Sk = 0, Ku = 0 พื้นที่ใต้โค้ง P( + 1 ) = 0.68 P( + 2 ) = 0.95 P( + 3 ) = 0.99 คุณสมบัติของโค้งการแจกแจงปกติ 8. 2 ) โค้งเบ้ทางบวก ( Positive Skewness) จำนวนคนที่ได้คะแนนต่ำมีจำนวนมาก คนที่ได้คะแนนสูงมีจำนวนน้อย Y X 9. 3) โค้งเบ้ทางลบ ( Negative Skewness) จำนวนคนที่ได้คะแนนสูงมีจำนวนมาก คนที่ได้คะแนนต่ำมีจำนวนน้อย Y X 10. 9.3 การวัดตำแหน่งเปรียบเทียบ (Measures of Relative Standing) 11. 1 ) อัตราส่วน (Ratio ) และสัดส่วน (Proportion ) อัตราส่วน เป็นการเปรียบเทียบความถี่ระหว่างรายการย่อยกับรายการย่อยของตัวแปร อัตราส่วน = ความถี่ของ A อัตราส่วน = ความถี่ของ A : ความถี่ของ B : ความถี่ของ C ความถี่ของ B 12. สัดส่วน เป็นการเปรียบเทียบความถี่ระหว่างรายการย่อยกับจำนวนทั้งหมดของตัวแปรนั้น สัดส่วน = ความถี่ของรายการ ความถี่ทั้งหมด 13. 2 ) ร้อยละ (Percent) ร้อยละ (Percent) เป็นการเปรียบเทียบความถี่ระหว่างรายการย่อยกับจำนวนทั้งหมดที่ ปรับเทียบให้เป็น 100 ค่าร้อยละจึงคำนวณเหมือนค่าสัดส่วนและปรับฐานให้เป็น 100 ร้อยละ = ความถี่ของรายการ x 100 ความถี่ทั้งหมด = สัดส่วน x 100 14. 3 ) ควอร์ไทล์ (Quartile) เดไซล์ (Decile) และเปอร์เซนไทล์ (Percentile) ควอร์ไทล์ ( Quartile) เป็นค่าที่แบ่งข้อมูลซึ่งเรียงตามขนาดออกเป็น 4 ส่วนเท่าๆกัน จึงมีค่าเป็น Q 1 , Q 2 และ Q 3 ตามลำดับ 15. เดไซล์ (Decile) เป็นค่าที่แบ่งข้อมูลเรียงตามขนาดออกเป็น 10 ส่วนเท่าๆกัน จึงมีค่าเป็น D 1 , D 2 , …, และ D 9 ตามลำดับ 16. เปอร์เซนไทล์ (Percentile) เป็นค่าที่แบ่งข้อมูลเรียงตามขนาดออกเป็น 100 ส่วนเท่าๆกัน จึงมีค่าเป็น P 1 , P 2 , …, และ P 99 ตามลำดับ 17. ความสัมพันธ์ระหว่างค่าควอร์ไทล์ (Q) เดไซล์ (D) และเปอร์เซนไทล์ (P) ค่าน้อย ค่ามาก Q 1 Q 2 Q 3 D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 P 1 P 10 P 20 P 30 P 40 P 50 P 60 P 70 P 80 P 90 P 100 18. 9.4 การวัดแนวโน้มเข้าสู่ส่วนกลาง และการวัดการกระจาย ( Measures of Central Tendency) 19. 20. 1) ฐานนิยม ( Mode) ฐานนิยม (Mo) ของชุดข้อมูลคือ ค่าที่มีความถี่สูงสุด หรือค่าที่เกิดขึ้นบ่อยครั้งที่สุด ข้อมูลบางชุดอาจมีค่าฐานนิยมมากกว่า 1 ค่า หรือไม่มีฐานนิยมก็ได้ 21. 2) มัธยฐาน (Median) มัธยฐาน (Med) ของชุดข้อมูล คือ ค่าที่อยู่ตรงกลาง หรือกึ่งกลางของตัวเลขที่เรียงลำดับ ค่ามัธยฐาน อาจเป็นค่ากลางที่ตรงกับค่าจริงของข้อมูลหรืออาจเป็นค่าเฉลี่ยของค่าที่อยู่ตรงกลาง 22. 3) ค่าเฉลี่ยเลขคณิต (Arithmetic Mean) ค่าเฉลี่ยเลขคณิต (AM) ของชุดข้อมูลคือ ค่าที่เกิดจากการรวมกันของข้อมูลทุกตัวแล้วหารด้วยจำนวนข้อมูล 23. 1) พิสัย (Range) พิสัย (R) ของชุดข้อมูล คือผลต่างระหว่างข้อมูลที่มีค่าสูงสุดกับข้อมูลที่มีค่าต่ำสุดของข้อมูลชุดนั้น 9.4.2 การวัดการกระจาย (Measures of Dispersion) 24. 2) ส่วนเบี่ยงเบนควอร์ไทล์ (Quartile Deviation) ส่วนเบี่ยงเบนควอร์ไทล์ (QD) คือ ครึ่งหนึ่งของความแตกต่างระหว่างระหว่างค่าควอร์ไทล์ที่ 3 กับค่าควอร์ไทล์ 1 QD = (Q3-Q1) / 2 25. 3. ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) ส่วนเบี่ยงเบนมาตรฐาน (S . D . หรือ S ) คือ ค่ารากที่สองของกำลังสองเฉลี่ยของส่วนเบี่ยงเบนระหว่างค่าของข้อมูลแต่ละตัวกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้น หรือเป็นค่ารากที่สองของส่วนเบี่ยงเบนกำลังสองเฉลี่ย S . D . = [ ( x - x )] 2 / N 26. 4) ความแปรปรวน ( Variance) ความแปรปรวนของข้อมูล (S 2 , 2 ) คือ ค่ากำลังสองของส่วนเบี่ยงเบนมาตรฐาน เมื่อ S, S 2 = สัญลักษณ์แทนส่วนเบี่ยงเบนมาตรฐาน และความแปรปรวนของข้อมูลกลุ่มตัวอย่างตามลำดับ เมื่อ , 2 = สัญลักษณ์แทนส่วนเบี่ยงเบนมาตรฐาน และความแปรปรวนของข้อมูลประชากรตามลำดับ 27. 5. สัมประสิทธ์การกระจาย (Coefficient of variation) สัมประสิทธิ์การกระจาย หรือ CV (%) เป็นค่าการกระจายของส่วนเบี่ยงเบนมาตรฐาน เมื่อกำหนดให้ค่าเฉลี่ยเลขคณิตเป็น 100 CV = (S . D . x 100) / X 28. 29. ที่มา คะแนนดิบแต่ละตัวไม่มีความหมายดีพอในการเปรียบเทียบ จึงได้นำคะแนนดิบไปหาความสัมพันธ์กับค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของ ข้อมูลชุดนั้นว่า คะแนนดิบแต่ละตัวอยู่ห่างจากค่ากลาง ( ค่าเฉลี่ย ) เป็นกี่เท่าของ ส่วนเบี่ยงเบนมาตรฐาน ( S.D. ) 30.






















![3. ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) ส่วนเบี่ยงเบนมาตรฐาน (S . D . หรือ S ) คือ ค่ารากที่สองของกำลังสองเฉลี่ยของส่วนเบี่ยงเบนระหว่างค่าของข้อมูลแต่ละตัวกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้น หรือเป็นค่ารากที่สองของส่วนเบี่ยงเบนกำลังสองเฉลี่ย S . D . = [ ( x - x )] 2 / N](https://image.slidesharecdn.com/res9-110806215052-phpapp02/85/slide-25-320.jpg)




