1. F-test

2. George W. Snedecor นักสถิติชาวอเมริกา เป็นผู้ใช้ชื่อนี้
ครั้งแรก โดยให้เกียรติแก่ Sir Ronald Aylmer Fisher
นักสถิติผู้ยิ่งใหญ่ชาวอังกฤษ ซึ่งเป็นผู้คิดค้นวิธีการทดสอบความ
แตกต่างกันหรือสัดส่วนของ Sum square ซึ่งใช้ใน
Analysis of Variance ที่ Fisher ได้คิดค้นมา
เพื่อแก้ไขจุดอ่อนของ Student's 2 samples T-test ใน
กรณีที่มีประชากรหรือตัวอย่างมากกว่า 2 กลุ่ม

3. ข้อตกลงเบื้องต้นของ F-test
1. กลุ่มตัวอย่างได้มาโดยการสุ่มที่เป็นอิสระจากกัน
2. ประชากรมีการแจกแจงแบบปกติ
3. ข้อมูลอยู่ในมาตราอันตรภาคหรืออัตราส่วน

4. ขั้นตอนการทดสอบ
1. กำหนดสมมติฐำน
2
2
2
11
2
2
2
10


:H
:H
2
2
2
1
2
2
2
11
2
2
2
10


หรือ:H
:H
2. กำหนดค่ำ 
3. คำนวณค่ำ F
2
2
2
1
s
s
F 
11 2211  ndfและndf

5. 4. กำหนดขอบเขตวิกฤต
เปิดตาราง 21 df,df,F
5. สรุปผลกำรทดสอบ
F  F วิกฤต จะปฏิเสธ Ho
F < F วิกฤต จะยอมรับ Ho

6. ตัวอย่ำงที่ 1 ผู้ซื้อสินค้าส่วนใหญ่มีความเชื่อว่า ราคาสินค้าในห้างสรรพสินค้าที่ไม่มีการ
แถมของจะมีความแปรปรวนมากกว่าห้างสรรพสินค้าที่มีการแถมของ จึงสอบถามราคา
สินค้าปรากฏผลดังนี้
ห้างที่ไม่มีการแถมของ 10 16 16 8 10 12
ห้างที่แถมของ 18 12 16 14
จงทดสอบว่าราคาสินค้าเป็นไปตามความเชื่อข้างต้นหรือไม่ ให้ = 0.05
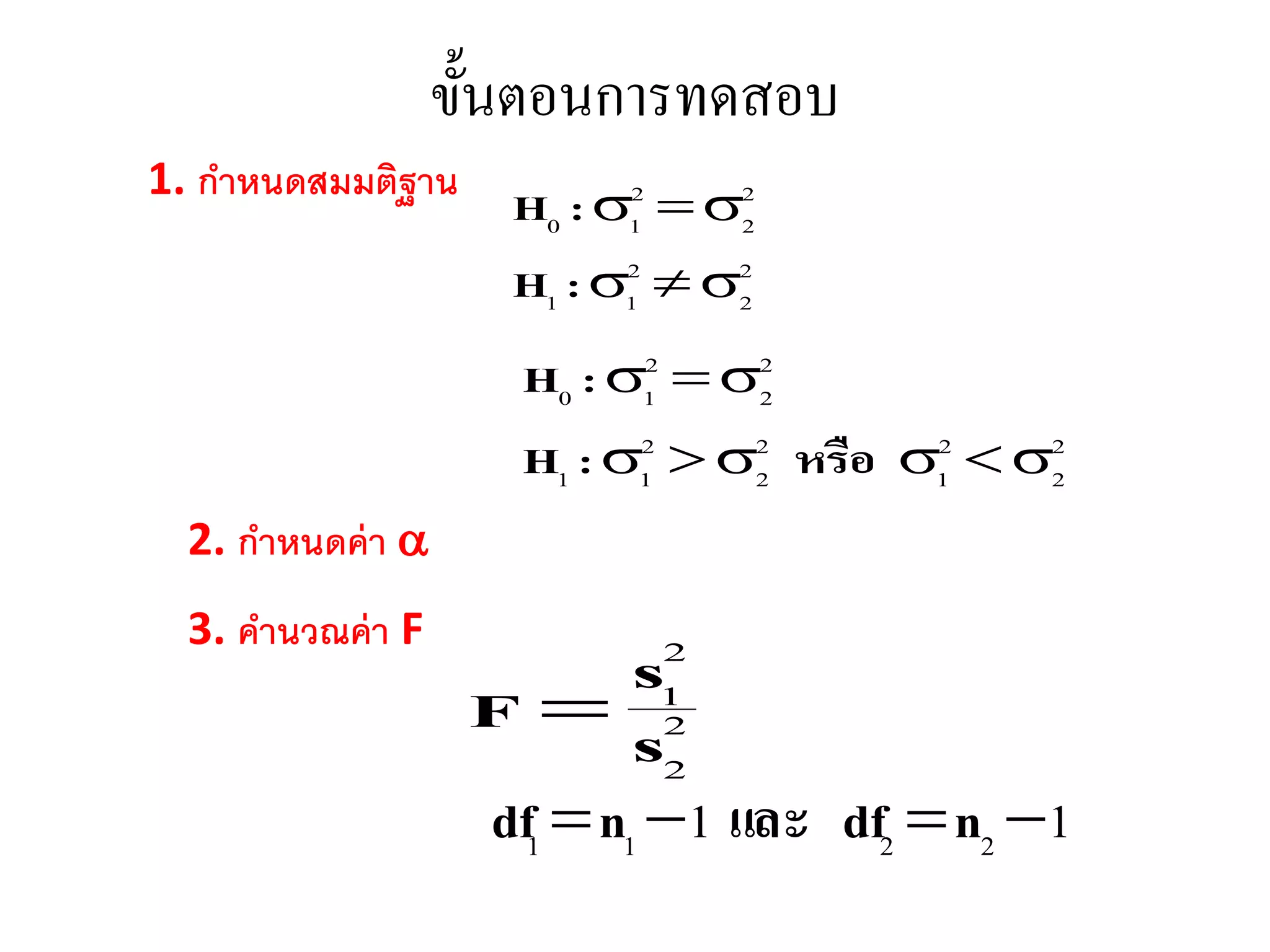
1. กำหนดสมมติฐำน
2
2
2
11
2
2
2
10


:H
:H
2. กำหนดค่ำ 
= 0.05

7. 3. คำนวณค่ำ F
2
2
2
1
s
s
F  11 2211  ndfและndf
1. ห้างที่ไม่มีการแถมของ 10 16 16 8 10 12 20112
1 .s 
2. ห้างที่แถมของ 18 12 16 14 6762
2 .s 
676
2011
.
.
F 
681.F
1416 21  df,df
35 21  df,df
4. กำหนดขอบเขตวิกฤต
เปิดตาราง 35050 ,,.F
01935050 .F ,,. 

8. 5. สรุปผลกำรทดสอบ
F < F วิกฤต จะยอมรับ Ho
2
2
2
10 :H
นั่นคือ ความเชื่อที่ว่าราคาสินค้าในห้างสรรพสินค้าที่ไม่มีการแถม
ของจะมีความแปรปรวนไม่มากกว่าห้างสรรพสินค้าที่มีการแถมของ
อย่างไม่มีนัยสาคัญทางสถิติที่ระดับ 0.05

9. ตัวอย่างที่ 2 จากการสุ่มตัวอย่าง 2 กลุ่ม กลุ่มแรกได้รับการสอนแบบ
บรรยาย และกลุ่มหลังสอนแบบอภิปราย ผลการทดลองปรากฏดังนี้
กลุ่มแรก ได้
กลุ่มหลัง ได้
20780
151162
222
111


n,s,x
n,s,x
แต่เนื่องจากผู้วิจัยไม่ทราบว่าจะใช้t-test แบบ Pooled Variance
หรือแบบ Separated Variance จึงจาเป็นต้องทดสอบว่า
ความแปรปรวนแตกต่างกันหรือไม่ ให้ = 0.05
1. กำหนดสมมติฐำน
2
2
2
11
2
2
2
10


:H
:H
2. กำหนดค่ำ 
= 0.05

10. 3. คำนวณค่ำ F
2
2
2
1
s
s
F  11 2211  ndfและndf
111 s 72 s
2
2
7
11
F
472.F 1914 21  df,df
4. กำหนดขอบเขตวิกฤต เปิดตาราง 1914050 ,,.F
2621914050 .F ,,. 
120115 21  dfและdf

11. 5. สรุปผลกำรทดสอบ
F > F วิกฤต จะปฎิเสธ Ho และยอมรับ H1
2
2
2
11 :H
สรุปว่า ความแปรปรวนของประชากรแตกต่างกันอย่างมีนัยสาคัญ
ทางสถิติที่ระดับ 0.05
นั่นคือ ผู้วิจัยจะต้องเลือกใช้สถิติทดสอบ t แบบ Separated Variance
)เมื่อ( 2
2
2
1 

13. ทดสอบท้ายบทเรียน
•ทาในห้องเรียน
•หมดเวลา 12.00 น.