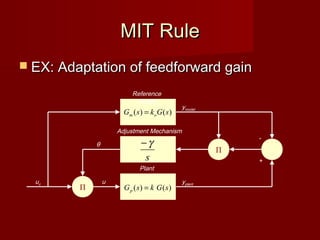
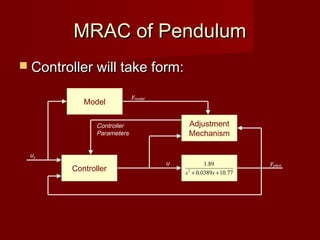
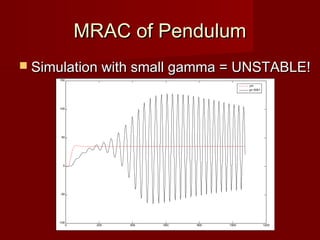
This document discusses model reference adaptive control (MRAC). It provides an overview of the concept, the MIT rule for updating controller parameters, and an example of applying MRAC to control the position of a pendulum. Simulation and experimental results show the controller requires proportional-derivative feedback and tuning to stabilize the unstable pendulum system. More advanced control methods could provide better practical performance than the basic MRAC approach presented.

1. Model ReferenceModel Reference
Adaptive ControlAdaptive Control
Survey of Control Systems (MEM 800)Survey of Control Systems (MEM 800)
Presented byPresented by
Keith SevcikKeith Sevcik

2. ConceptConcept
 Design controller to drive plant response to mimic idealDesign controller to drive plant response to mimic ideal
response (error = yresponse (error = yplantplant-y-ymodelmodel => 0)=> 0)
 Designer chooses: reference model, controller structure,Designer chooses: reference model, controller structure,
and tuning gains for adjustment mechanismand tuning gains for adjustment mechanism
Controller
Model
Adjustment
Mechanism
Plant
Controller
Parameters
ymodel
u yplant
uc

3. MIT RuleMIT Rule
 Tracking error:Tracking error:
 Form cost function:Form cost function:
 Update rule:Update rule:
– Change in is proportional to negative gradient ofChange in is proportional to negative gradient of
modelplant yye −=
)(
2
1
)( 2
θθ eJ =
δθ
δ
γ
δθ
δ
γ
θ e
e
J
dt
d
−=−=
θ J
sensitivity
derivative

4. MIT RuleMIT Rule
 Can chose different cost functionsCan chose different cost functions
 EX:EX:
 From cost function and MIT rule, control law can beFrom cost function and MIT rule, control law can be
formedformed





<−
=
>
=
−=
=
0,1
0,0
0,1
)(where
)(
)()(
e
e
e
esign
esign
e
dt
d
eJ
δθ
δ
γ
θ
θθ

5. MIT RuleMIT Rule
 EX: Adaptation of feedforward gainEX: Adaptation of feedforward gain
Adjustment Mechanism
ymodel
u yplantuc
Π
Π
θ
Reference
Model
Plant
s
γ−
)()( sGksG om =
)()( sGksGp =
-
+

6. MIT RuleMIT Rule
 For system where is unknownFor system where is unknown
 Goal: Make it look likeGoal: Make it look like
using plant (note, plant model isusing plant (note, plant model is
scalar multiplied by plant)scalar multiplied by plant)
)(
)(
)(
skG
sU
sY
= k
)(
)(
)(
sGk
sU
sY
o
c
=
)()( sGksG om =

7. MIT RuleMIT Rule
 Choose cost function:Choose cost function:
 Write equation for error:Write equation for error:
 Calculate sensitivity derivative:Calculate sensitivity derivative:
 Apply MIT rule:Apply MIT rule:
coccmm UGkUkGUGkGUyye −=−=−= θ
δθ
δ
γ
θ
θθ
e
e
dt
d
eJ −=→= )(
2
1
)( 2
m
o
c y
k
k
kGU
e
==
δθ
δ
eyey
k
k
dt
d
mm
o
γγ
θ
−=−= '

8. MIT RuleMIT Rule
 Gives block diagram:Gives block diagram:
 considered tuning parameterconsidered tuning parameter
Adjustment Mechanism
ymodel
u yplantuc
Π
Π
θ
Reference
Model
Plant
s
γ−
)()( sGksG om =
)()( sGksGp =
-
+
γ

9. MIT RuleMIT Rule
 NOTE: MIT rule does not guarantee errorNOTE: MIT rule does not guarantee error
convergence or stabilityconvergence or stability
 usually kept smallusually kept small
 Tuning crucial to adaptation rate andTuning crucial to adaptation rate and
stability.stability.
γ
γ

10.  SystemSystem
MRAC of PendulumMRAC of Pendulum
( ) TdmgdcJ c 1sin =++ θθθ 
cmgdcsJs
d
sT
s
++
= 2
1
)(
)(θd2
d1dc
T
77.100389.0
89.1
)(
)(
2
++
=
sssT
sθ

11. MRAC of PendulumMRAC of Pendulum
 Controller will take form:Controller will take form:
Controller
Model
Adjustment
Mechanism
Controller
Parameters
ymodel
u yplant
uc
77.100389.0
89.1
2
++ ss

12. MRAC of PendulumMRAC of Pendulum
 Following process as before, writeFollowing process as before, write
equation for error, cost function, andequation for error, cost function, and
update rule:update rule:
modelplant yye −=
)(
2
1
)( 2
θθ eJ =
δθ
δ
γ
δθ
δ
γ
θ e
e
J
dt
d
−=−=
sensitivity
derivative

13. MRAC of PendulumMRAC of Pendulum
 Assuming controller takes the form:Assuming controller takes the form:
( )
cplant
plantcpplant
cmpmodelplant
plantc
u
ss
y
yu
ss
uGy
uGuGyye
yuu
2
2
1
212
21
89.177.100389.0
89.1
77.100389.0
89.1
θ
θ
θθ
θθ
+++
=
−





++
==
−=−=
−=

14. MRAC of PendulumMRAC of Pendulum
( )
plant
c
c
cmc
y
ss
u
ss
e
u
ss
e
uGu
ss
e
2
2
1
2
2
2
1
2
2
2
2
1
2
2
1
89.177.100389.0
89.1
89.177.100389.0
89.1
89.177.100389.0
89.1
89.177.100389.0
89.1
θ
θ
θ
θ
θ
θθ
θ
θ
+++
−=
+++
−=
∂
∂
+++
=
∂
∂
−
+++
=

15. MRAC of PendulumMRAC of Pendulum
 If reference model is close to plant, canIf reference model is close to plant, can
approximate:approximate:
plant
mm
mm
c
mm
mm
mm
y
asas
asae
u
asas
asae
asasss
01
2
01
2
01
2
01
1
01
2
2
2
89.177.100389.0
++
+
−=
∂
∂
++
+
=
∂
∂
++≈+++
θ
θ
θ

16. MRAC of PendulumMRAC of Pendulum
 From MIT rule, update rules are then:From MIT rule, update rules are then:
ey
asas
asa
e
e
dt
d
eu
asas
asa
e
e
dt
d
plant
mm
mm
c
mm
mm






++
+
=
∂
∂
−=






++
+
−=
∂
∂
−=
01
2
01
2
2
01
2
01
1
1
γ
θ
γ
θ
γ
θ
γ
θ

17. MRAC of PendulumMRAC of Pendulum
 Block DiagramBlock Diagram
ymodel
e
yplantuc
Π
Π
θ1
Reference
Model
Plant
s
γ−
77.100389.0
89.1
2
++ ss
Π
+
-
mm
mm
asas
asa
01
2
01
++
+
mm
mm
asas
asa
01
2
01
++
+
mm
m
asas
b
01
2
++
s
γ
Π
-
+
θ2

18. MRAC of PendulumMRAC of Pendulum
 Simulation block diagram (NOTE:Simulation block diagram (NOTE:
Modeled to reflect control of DC motor)Modeled to reflect control of DC motor)
am
s+am
am
s+am
-gamma
s
gamma
s
Step
Saturation
omega^2
s+am
Reference Model
180/pi
Radians
to Degrees
4.41
s +.039s+10.772
Plant
2/26
Degrees
to Volts
35
Degrees
y m
Error
Theta2
Theta1
y

19. MRAC of PendulumMRAC of Pendulum
 Simulation with small gamma = UNSTABLE!Simulation with small gamma = UNSTABLE!
0 200 400 600 800 1000 1200
-100
-50
0
50
100
150
ym
g=.0001

20. MRAC of PendulumMRAC of Pendulum
 Solution: Add PD feedbackSolution: Add PD feedback
am
s+am
am
s+am
-gamma
s
gamma
s
Step
Saturation
omega^2
s+am
Reference Model
180/pi
Radians
to Degrees
4.41
s +.039s+10.772
Plant
1
P
du/dt
2/26
Degrees
to Volts
35
Degrees
1.5
D
y m
Error
Theta2
Theta1
y

21. MRAC of PendulumMRAC of Pendulum
 Simulation results with varying gammasSimulation results with varying gammas
0 500 1000 1500 2000 2500
0
5
10
15
20
25
30
35
40
45
ym
g=.01
g=.001
g=.0001
707.
sec3
:such thatDesigned
56.367.2
56.3
2
=
=
++
=
ζ
s
m
T
ss
y

22. LabVIEW VI Front PanelLabVIEW VI Front Panel

23. LabVIEW VI Back PanelLabVIEW VI Back Panel

24. Experimental ResultsExperimental Results

25. Experimental ResultsExperimental Results
 PD feedback necessary to stabilizePD feedback necessary to stabilize
systemsystem
 Deadzone necessary to prevent updatingDeadzone necessary to prevent updating
when plant approached modelwhen plant approached model
 Often went unstable (attributed to inherentOften went unstable (attributed to inherent
instability in system i.e. little damping)instability in system i.e. little damping)
 Much tuning to get acceptable responseMuch tuning to get acceptable response

26. ConclusionsConclusions
 Given controller does not perform well enoughGiven controller does not perform well enough
for practical usefor practical use
 More advanced controllers could be formed fromMore advanced controllers could be formed from
other methodsother methods
– Modified (normalized) MITModified (normalized) MIT
– Lyapunov direct and indirectLyapunov direct and indirect
– Discrete modeling using Euler operatorDiscrete modeling using Euler operator
 Modified MRAC methodsModified MRAC methods
– Fuzzy-MRACFuzzy-MRAC
– Variable Structure MRAC (VS-MRAC)Variable Structure MRAC (VS-MRAC)