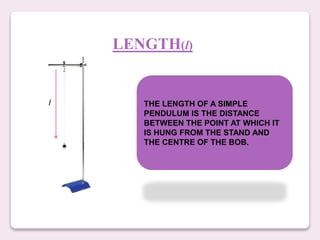
Galileo Galilei discovered the simple pendulum in the early 1600s. A simple pendulum consists of a point mass suspended by an inextensible thread with no friction that is free to oscillate. The key factors that determine a simple pendulum's motion are its length, mass, oscillation, equilibrium position, amplitude, period, and frequency. The period and frequency are inversely related, with the period being the time for one full oscillation and the frequency being the number of oscillations per second.

4. SIMPLE PENDULUM

5.  DISCOVERED BY
GALILEO GALILEI
ITALIAN SCIENTIST
STUDIED ABOUT
PROPERTIES OF
PENDULUMS

6. DEFINITION OF SIMPLE PENDULUM:
AN IDEAL PENDULUM CONSISTING OF
A POINT MASS SUSPENDED BY A WEIGHTLESS
INEXTENSIBLE PERFECTLY FLEXIBLE THREAD AND
FREE TO VIBRATE WITHOUT FRICTION.

7. PARTS OF THE SIMPLE
PENDULUM
 LENGTH
 MASS OF THE BOB

8. FACTORS OF SIMPLE
PENDULUM
OSCILLATION
EQUILIBRIUM POSITION
AMPLITUDE
PERIOD
FREQUENCY

9. THE LENGTH OF A SIMPLE
PENDULUM IS THE DISTANCE
BETWEEN THE POINT AT WHICH IT
IS HUNG FROM THE STAND AND
THE CENTRE OF THE BOB.
l
LENGTH(l)

10. WE CAN USE METAL BALL AS THE BOB.
MASS OF THE BOB(m):

11. OSCILLATION IS THE TO AND FRO MOTION OF
THE PENDULUM ABOUT A FIXED POINT.
A B
O
THE BOB COMPLETES ONE OSCILLATION WHEN
IT SWINGS FROM ‘O’ TO ‘B’ THEN TO ‘A’ AND
RETURNS TO ‘O’.
OSCILLATION

12. WHEN THE PENDULUM IS
AT REST,IT IS SAID TO BE
IN EQULUBRIUM.
EQUILIBRIUM
POSITION
O
THE POSITION ‘O’ IS THE
EQUILIBRIUM POSITION

13. AMPLITUDE
THE MAXIMUM DISPLACEMENT
OF THE BOB FROM THE
EQUILIBRIUM POSITION IS ITS
AMPLITUDE

14. PERIOD (T)
THE TIME TAKEN FOR ONE
OSCILLATION IS THE PERIOD
 TIME TAKEN FOR A DEFINITE NUMBER OF OSCILLATIONS (t)
NUMBER OF OSCILLATIONS (n)
T = t/n

15. FREQUENCY (f)
FREQUENCY IS THE NUMBER OF
OSCILLATIONS PER SECOND
F =
n/t

16. RELATION BETWEEN PERIOD AND
FREQUENCY
T= t/n 1
F =
n/t
2
T = 1/
f
f= 1/T
TAKING RECIPROCALS OF BOTH
EQUATIONS, WE GET…..
The period T is the reciprocal of the
frequency & Vice versa

17. EXAMPLES FOR SIMPLE
PENDULUM