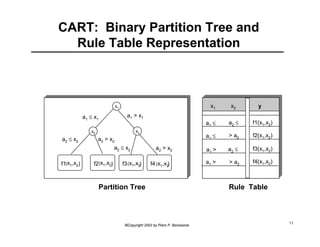
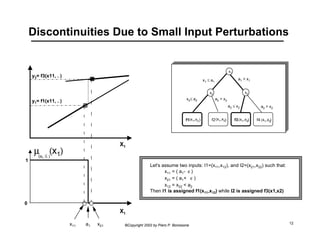
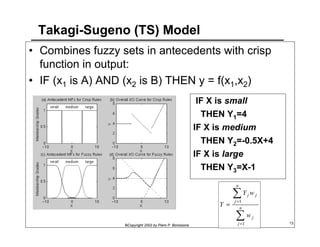
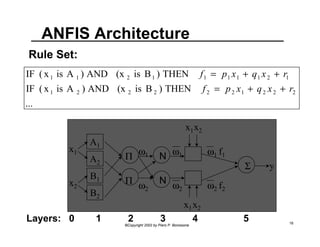
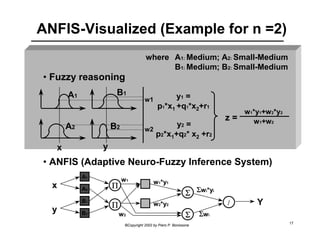
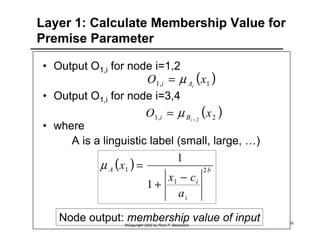
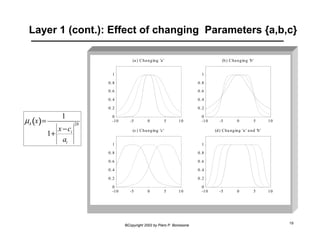
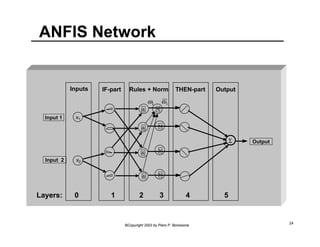
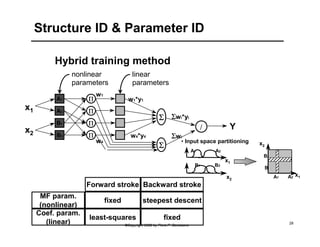
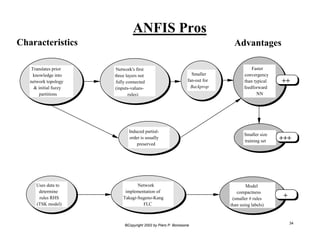
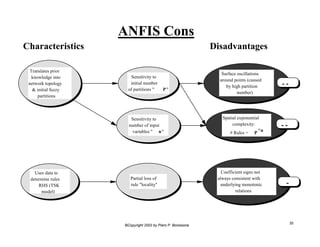
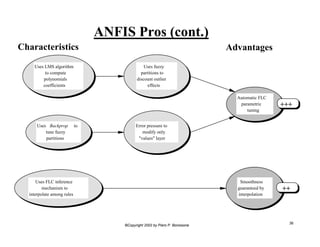
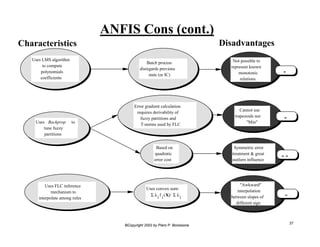
This document provides an overview of Adaptive Neural Fuzzy Inference Systems (ANFIS). It discusses how ANFIS aims to integrate the benefits of fuzzy systems and neural networks by using neural network learning methods to determine the parameters of fuzzy inference systems. The document outlines ANFIS architecture and computational complexity. It also describes how ANFIS uses a hybrid learning algorithm with a least squares estimate to identify linear parameters and backpropagation to adjust nonlinear parameters.

1. Adaptive Neural Fuzzy
Inference Systems (ANFIS):
Analysis and Applications
©Copyright 2002 by Piero P. Bonissone 1

2. ©Copyright 2002 by Piero P. Bonissone 2
Outline
• Objective
• Fuzzy Control
– Background, Technology & Typology
• ANFIS:
– as a Type III Fuzzy Control
– as a fuzzification of CART
– Characteristics
– Pros and Cons
– Opportunities
– Applications
– References

3. ANFIS Objective
• To integrate the best features of Fuzzy
Systems and Neural Networks:
– From FS: Representation of prior knowledge into
a set of constraints (network topology) to reduce
the optimization search space
– From NN: Adaptation of backpropagation to
structured network to automate FC parametric
tuning
• ANFIS application to synthesize:
– controllers (automated FC tuning)
– models (to explain past data and predict future
behavior)
©Copyright 2002 by Piero P. Bonissone 3

4. FC Technology & Typology
• Fuzzy Control
– A high level representation language with
local semantics and an interpreter/compiler
to synthesize non-linear (control) surfaces
– A Universal Functional Approximator
• FC Types
– Type I: RHS is a monotonic function
– Type II: RHS is a fuzzy set
– Type III: RHS is a (linear) function of state
©Copyright 2002 by Piero P. Bonissone 4

5. FC Technology (Background)
• Fuzzy KB representation
– Scaling factors, Termsets, Rules
• Rule inference (generalized modus ponens)
• Development & Deployment
– Interpreters, Tuners, Compilers, Run-time
– Synthesis of control surface
• FC Types I, II, III
©Copyright 2002 by Piero P. Bonissone 5

6. FC of Type II, III, and ANFIS
• Type II Fuzzy Control must be tuned manually
• Type III Fuzzy Control (Takagi-Sugeno type)
have an automatic Right Hand Side (RHS)
tuning
• ANFIS will provide both:
– RHS tuning, by implementing the TSK controller
as a network
– and LHS tuning, by using back-propagation
©Copyright 2002 by Piero P. Bonissone 6

7. Inputs IF-part Rules + Norm THEN-part Output
N
©Copyright 2002 by Piero P. Bonissone 7
x1
x2
Input 1
Input 2
&
&
&
&
Σ Output
ANFIS Network
N
N
N
ω1
1 ω
Layers: 0 1 2 3 4 5

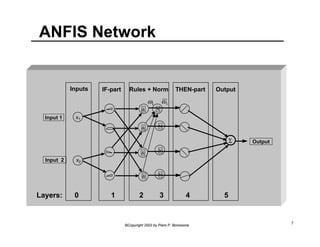
8. ANFIS Neurons: Clarification note
• Note that neurons in ANFIS have different
structures:
– Values [ Membership function defined by parameterized
soft trapezoids (Generalized Bell Functions) ]
– Rules [ Differentiable T-norm - usually product ]
– Normalization [ Sum and arithmetic division ]
– Functions [ Linear regressions and multiplication with
, i.e., normalized weights ω, ]
– Output [ Algebraic Sum ]
©Copyright 2002 by Piero P. Bonissone 8
ω

9. ANFIS as a generalization of CART
• Classification and Regression Tree (CART)
– Algorithm defined by Breiman et al in 1984
– Creates a binary decision tree to classify the
data into one of 2n linear regression models to
minimize the Gini index for the current node c:
Gini(c) =
2
j Σ
1 − pj
where:
• pj is the probability of class j in node c
• Gini(c) measure the amount of “impurity” (incorrect
classification) in node c
©Copyright 2002 by Piero P. Bonissone 9

10. CART Problems
• Discontinuity
• Lack of locality (sign of coefficients)
©Copyright 2002 by Piero P. Bonissone 10

11. CART: Binary Partition Tree and
Rule Table Representation
x1 x2 y
a1 ≤ a2 ≤ f1(x1,x2)
a1 ≤ > a2
f2(x1,x2)
a1 > a2 ≤
f3(x1,x2)
a1> > a2
f4(x1,x2)
a1 ≤ x1
a1 > x1
a2 ≤ x2 a2 > x2
a2 > x2 a2 ≤ x2
Partition Tree Rule Table
©Copyright 2002 by Piero P. Bonissone 11
x1
x2 x2
f1(x1,x2) f2(x1,x2) f3(x1,x2) f4 (x1,x2)

12. Discontinuities Due to Small Input Perturbations
x1 ≤ a1
a1 > x1
x2≤ a2 a2 > x2
a2 > x2 a2 ≤ x2
Let's assume two inputs: I1=(x11,x12), and I2=(x21,x22) such that:
x11 = ( a1- ε )
x21 = ( a1+ ε )
x12 = x22 < a2
Then I1 is assigned f1(x11,x12) while I2 is assigned f3(x1,x2)
X1
©Copyright 2002 by Piero P. Bonissone 12
y1= f1(x11, . )
(a1 ≤ ) μ (x1)
x11 a1 x21
y3= f3(x11, . )
1
0
X1
x1
x2 x2
f1(x1,x2) f2(x1,x2) f3 (x1,x2) f4 (x1,x2)

13. Takagi-Sugeno (TS) Model
• Combines fuzzy sets in antecedents with crisp
function in output:
• IF (x1
is A) AND (x2 is B) THEN y = f(x1,x2)
IF X is small
THEN Y1=4
IF X is medium
THEN Y2=-0.5X+4
IF X is large
THEN Y3=X-1
Σ
= =n
Y w
Σ
=
©Copyright 2002 by Piero P. Bonissone j
13
j
n
j
j j
w
Y
1
1

14. ANFIS Characteristics
• Adaptive Neural Fuzzy Inference System
(ANFIS)
– Algorithm defined by J.-S. Roger Jang in 1992
– Creates a fuzzy decision tree to classify the data
into one of 2n (or pn) linear regression models to
minimize the sum of squared errors (SSE):
j Σ
SSE = ej 2
©Copyright 2002 by Piero P. Bonissone 14
where:
• ej is the error between the desired and the actual output
• p is the number of fuzzy partitions of each variable
• n is the number of input variables

15. ANFIS as a Type III FC
• L0: State variables are nodes in ANFIS inputs layer
• L1: Termsets of each state variable are nodes in
ANFIS values layer, computing the membership
value
• L2: Each rule in FC is a node in ANFIS rules layer
using soft-min or product to compute the rule
matching factor ωi
• L3: Each ωi
is scaled into in the normalization layer
i ω
• L4: Each weighs the result of its linear regression fi
in the function layer, generating the rule output
• L5: Each rule output is added in the output layer
©Copyright 2002 by Piero P. Bonissone 15
i ω

16. ANFIS Architecture
Rule Set:
IF ( x is A ) AND (x is B ) THEN
= + +
f p x q x r
1 1 2 1 1 1 1 1 2 1
IF ( x is A ) AND (x is B ) THEN
= + +
f p x q x r
x2
©Copyright 2002 by Piero P. Bonissone 16
...
1 2 2 2 2 2 1 2 2 2
x1
x2
A1
A2
B1
B2
Π
Π
ω N 1
ω2
N
ω1
ω2
ω1 f1
ω2 f2
Σ y
x1
x1 x2
Layers: 0 1 2 3 4 5

17. ANFIS-Visualized (Example for n =2)
• Fuzzy reasoning
A1 B1
where A1: Medium; A2: Small-Medium
B1: Medium; B2: Small-Medium
w1*y1+w2*y2
©Copyright 2002 by Piero P. Bonissone 17
A2 B2
w1
w2
y1 =
p1*x1 +q1*x2+r1
y2 =
p2*x1+q2* x2 +r2
z = w1+w2
x y
• ANFIS (Adaptive Neuro-Fuzzy Inference System)
A1
A2
B1
B2
Π
Π
Σ
Σ
/
x
y
w1
w2
w1*y1
w2*y2
Σwi*yi
Σwi
Y

18. Layer 1: Calculate Membership Value for
Premise Parameter
• Output O1,i for node i=1,2
( ) 1, 1 O x
i Ai = μ
• Output O1,i for node i=3,4
( ) 1, 2 2
i Bi − = μ
O x
x 2
x c
©Copyright 2002 by Piero P. Bonissone 18
• where
A is a linguistic label (small, large, …)
( ) b
i
i
A
a
1
1
1
1
+ −
μ =
Node output: membership value of input

19. Layer 1 (cont.): Effect of changing Parameters {a,b,c}
(a ) Cha nging 'a '
1
0.8
0.6
0.4
0.2
0
(b) Cha nging 'b'
(c ) Cha nging 'c '
1
0.8
0.6
0.4
0.2
0
(d) Cha nging 'a ' a nd 'b'
©Copyright 2002 by Piero P. Bonissone 19
μA
(x)= 1
1+ x −ci
ai
2b
1
0.8
0.6
0.4
0.2
0
-10 -5 0 5 10
-10 -5 0 5 10
1
0.8
0.6
0.4
0.2
0
-10 -5 0 5 10
-10 -5 0 5 10

20. Layer 2: Firing Strength of Rule
• Use T-norm (min, product, fuzzy AND, ...)
( ) ( ) 2, 1 2 O w x x
i i Ai Bi = = μ μ
(for i=1,2)
Node output: firing strength of rule
©Copyright 2002 by Piero P. Bonissone 20

21. Layer 3: Normalize Firing Strength
• Ratio of ith rule’s firing strength vs. all
rules’ firing strength
O w
w
i
i i w w
(for i=1,2)
©Copyright 2002 by Piero P. Bonissone 21
3
1 2
, = =
+
Node output: Normalized firing strengths

22. Layer 4: Consequent Parameters
• Takagi-Sugeno type output
( )i i i i i i i O = w f = w p x + q x + r 4, 1 2
• Consequent parameters {pi, qi, ri}
Node output: Evaluation of Right Hand
Side Polynomials
©Copyright 2002 by Piero P. Bonissone 22

23. Layer 5: Overall Output
Σ
Σ
w f
w i i
5,1= Σ =
O wf
i
i i
i
i
i
2
2
w
+
w w
1 2
f
f
w
+
w w
+
= + + + + +
w p x q x r w p x q x r
= + + + + +
©Copyright 2002 by Piero P. Bonissone 23
• Note:
– Output is linear in consequent parameters p,q,r:
1
1
1 2
1 ( 1 1 1 2 1 ) 2 ( 2 1 2 2 2
)
( w 1 x 1 ) p 1 ( w 1 x 2 ) q 1 ( w 1 ) r 1 ( w 2 x 1 ) p 2 ( w 2 x 2 ) q 2 ( w 2 )r
2
=
Node output: Weighted Evaluation of RHS Polynomials

24. Inputs IF-part Rules + Norm THEN-part Output
N
©Copyright 2002 by Piero P. Bonissone 24
x1
x2
Input 1
Input 2
&
&
&
&
Σ Output
ANFIS Network
N
N
N
ω1
1 ω
Layers: 0 1 2 3 4 5

25. ANFIS Computational Complexity
Layer # L-Type # Nodes # Param
L0 Inputs n 0
L1 Values (p•n) 3•(p•n)=|S1|
L2 Rules pn 0
L3 Normalize pn 0
L4 Lin. Funct. pn (n+1)•pn=|S2|
L5 Sum 1 0
©Copyright 2002 by Piero P. Bonissone 25

26. ANFIS Parametric Representation
• ANFIS uses two sets of parameters: S1 and S2
– S1 represents the fuzzy partitions used in the
rules LHS
S1= a11,b11,c11 { }, a12,b12,c12 { },..., a1p,b1p,c1p { },..., anp,bnp,cnp { { }}
– S2 represents the coefficients of the linear
functions in the rules RHS
S2 = c10,c11,...,c1n { },..., cpn 0 ,cpn1,...,cpnn { { }}
©Copyright 2002 by Piero P. Bonissone 26

27. ANFIS Learning Algorithms
• ANFIS uses a two-pass learning cycle
©Copyright 2002 by Piero P. Bonissone 27
– Forward pass:
• S1 is fixed and S2 is computed using a Least
Squared Error (LSE) algorithm (Off-line Learning)
– Backward pass:
• S2 is fixed and S1 is computed using a gradient
descent algorithm (usually Back-propagation)

28. Structure ID & Parameter ID
Hybrid training method
Forward stroke Backward stroke
B2
©Copyright 2002 by Piero P. Bonissone 28
A1
A2
B1
B2
Σ
Σ
/
x1
nonlinear
parameters
w1
w4
w1*y1
w4*y4
Σwi*yi
Σwi
Y
Π
Π
Π
Π
linear
parameters
fixed
least-squares
steepest descent
fixed
MF param.
(nonlinear)
Coef. param.
(linear)
• Input space partitioning
A1
B1
A2
B2
x1
x1
x2
A1 A2
B1
x2
x2

29. ANFIS Least Squares (LSE) Batch Algorithm
• LSE used in Forward Stroke:
S = {S1US2}, and{S1IS2 = ∅}
Output = F(I ,S),where I is the input vector
H(Output ) = H o F(I , S ),where H o F is linear in S2
©Copyright 2002 by Piero P. Bonissone 29
– Parameter Set:
– For given values of S1, using K training data, we
can transform the above equation into B=AX,
where X contains the elements of S2
– This is solved by: (ATA)-1AT B=X* where (ATA)-1AT
is the pseudo-inverse of A (if ATA is nonsingular)
– The LSE minimizes the error ||AX-B||2 by
approximating X with X*

30. ANFIS LSE Batch Algorithm (cont.)
• Rather than solving directly (ATA)-1AT B=X* , we
resolve it iteratively (from numerical methods):
T Si
T Sia(i+1)
T − a(i+1)







©Copyright 2002 by Piero P. Bonissone 30
Si+1 = Si −
Sia(i+1)a(i+1)
1 + a(i+1)
,
Xi+1 = Xi + S(i+1)a(i+1)(b(i+1)
T Xi )



for i = 0,1,...,K −1
X0 = 0,
S0 = γ I , (where γ is a large number )
a i
T = ith line of matrix A
bi
T = ith element of vector B
X* = Xk
where:

31. ANFIS Back-propagation
• Error measure Ek
(for the kth (1≤k≤K) entry of the training data)
( )
E k = Σ=
d i −
x ( )2
,
N L
1
L i
i
N(L) = number nodes in layer L
i component of output vector
d desired
KΣ vector output of component i
i
• Overall error measure E:
E = E k
k = 1
©Copyright 2002 by Piero P. Bonissone 31
where :
th
,
th
x actual
L i
=
=

32. ANFIS Back-propagation (cont.)
• For each parameter αi the update formula is:
E
i
α η ∂
Δ = −
i
+
∂α
is the learning rate
η κ
∂


is the step size
is the ordered derivative
©Copyright 2002 by Piero P. Bonissone 32
where :
i
2
i
i
E
E
κ
∂
∂α
∂α
+
Σ  
 
=

33. ANFIS Pros and Cons
• ANFIS is one of the best tradeoff between
neural and fuzzy systems, providing:
– smoothness, due to the FC interpolation
– adaptability, due to the NN Backpropagation
• ANFIS however has strong computational
complexity restrictions
©Copyright 2002 by Piero P. Bonissone 33

34. ANFIS Pros
Characteristics Advantages
++
©Copyright 2002 by Piero P. Bonissone 34
Translates prior
knowledge into
network topology
& initial fuzzy
partitions
Network's first
three layers not
fully connected
(inputs-values-rules)
Induced partial-order
is usually
preserved
Uses data to
determine
rules RHS
(TSK model)
Network
implementation of
Takagi-Sugeno-Kang
FLC
Smaller
fan-out for
Backprop
Faster
convergency
than typical
feedforward
NN
Smaller size
training set
Model
compactness
(smaller # rules
than using labels)
+++
+

35. Characteristics Disadvantages
- -
©Copyright 2002 by Piero P. Bonissone 35
Translates prior
knowledge into
network topology
& initial fuzzy
partitions
ANFIS Cons
Sensitivity to
initial number
of partitions " P"
Uses data to
determine rules
RHS (TSK
model)
Partial loss of
rule "locality"
Surface oscillations
around points (caused
by high partition
number)
Coefficient signs not
always consistent with
underlying monotonic
relations
Sensitivity to
number of input
variables " n"
Spatial exponential
complexity:
# Rules = P^n
- -
-

36. Characteristics Advantages
+++
©Copyright 2002 by Piero P. Bonissone 36
Uses LMS algorithm
to compute
polynomials
coefficients
Uses Backprop to
tune fuzzy
partitions
Uses fuzzy
partitions to
discount outlier
effects
Automatic FLC
parametric
tuning
Error pressure to
modify only
"values" layer
Smoothness
guaranteed by
interpolation
ANFIS Pros (cont.)
Uses FLC inference
mechanism to
interpolate among rules
++

37. ANFIS Cons (cont.)
Characteristics Disadvantages
©Copyright 2002 by Piero P. Bonissone 37
Uses LMS algorithm
to compute
polynomials
coefficients
Uses Backprop to
tune fuzzy
partitions
Batch process
disregards previous
state (or IC)
Uses FLC inference
mechanism to
interpolate among rules
Not possible to
represent known
monotonic
relations
Error gradient calculation
requires derivability of
fuzzy partitions and
T-norms used by FLC
Uses convex sum:
Σ λi f i (X)/ Σ λ i
Cannot use
trapezoids nor
"Min"
"Awkward"
interpolation
between slopes of
different sign
Based on
quadratic
error cost
function
Symmetric error
treatment & great
outliers influence
-
-
- -
-

38. ANFIS Opportunities
• Changes to decrease ANFIS complexity
– Use “don’t care” values in rules (no connection
between any node of value layer and rule layer)
– Use reduced subset of state vector in partition tree
while evaluating linear functions on complete state
– Use heterogeneous partition granularity (different
partitions pi for each state variable, instead of “p”)
nΠ
# RULES = pi
i=1
©Copyright 2002 by Piero P. Bonissone 38
X
= (XrU X(n−r) )

39. ANFIS Opportunities (cont.)
• Changes to extend ANFIS applicability
– Use other cost function (rather than SSE) to
represent the user’s utility values of the error
(error asymmetry, saturation effects of
outliers,etc.)
– Use other type of aggregation function (rather than
convex sum) to better handle slopes of different
signs.
©Copyright 2002 by Piero P. Bonissone 39

40. ANFIS Applications at GE
• Margoil Oil Thickness Estimator
• Voltage Instability Predictor (Smart Relay)
• Collateral Evaluation for Mortgage Approval
• Prediction of Time-to-Break for Paper Web
©Copyright 2002 by Piero P. Bonissone 40

41. ANFIS References
• “ANFIS: Adaptive-Network-Based Fuzzy Inference System”,
J.S.R. Jang, IEEE Trans. Systems, Man, Cybernetics,
23(5/6):665-685, 1993.
• “Neuro-Fuzzy Modeling and Control”, J.S.R. Jang and C.-T.
Sun, Proceedings of the IEEE, 83(3):378-406
• “Industrial Applications of Fuzzy Logic at General Electric”,
Bonissone, Badami, Chiang, Khedkar, Marcelle, Schutten,
Proceedings of the IEEE, 83(3):450-465
• The Fuzzy Logic Toolbox for use with MATLAB, J.S.R. Jang
and N. Gulley, Natick, MA: The MathWorks Inc., 1995
• Machine Learning, Neural and Statistical Classification
Michie, Spiegelhart & Taylor (Eds.), NY: Ellis Horwood 1994
• Classification and Regression Trees, Breiman, Friedman,
Olshen & Stone, Monterey, CA: Wadsworth and Brooks, 1985
©Copyright 2002 by Piero P. Bonissone 41