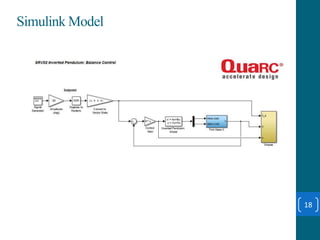
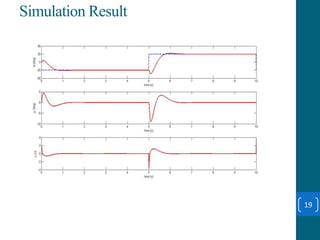
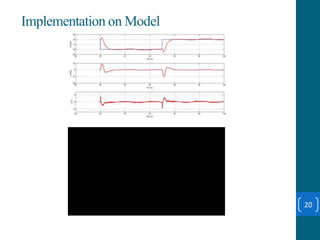
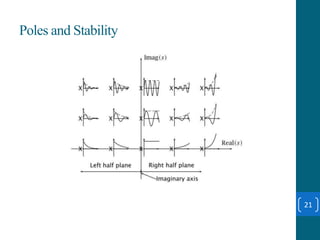
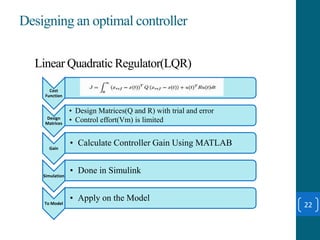
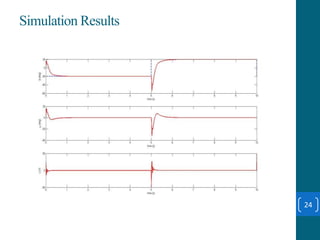
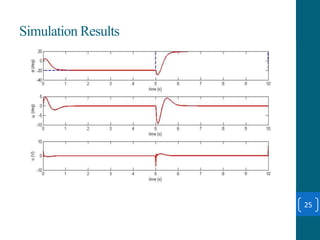
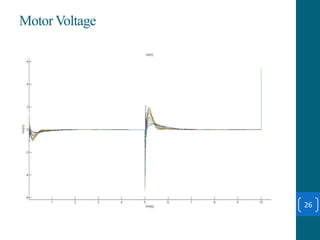
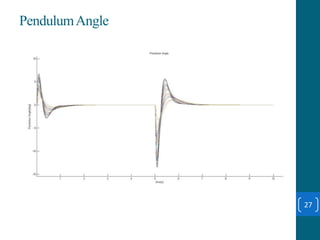
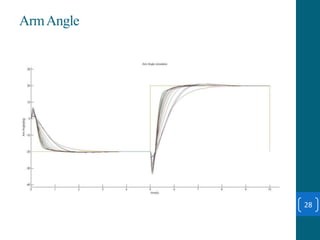
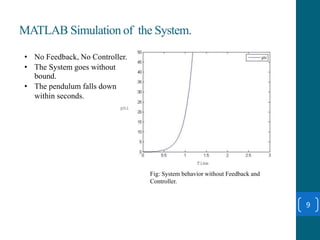
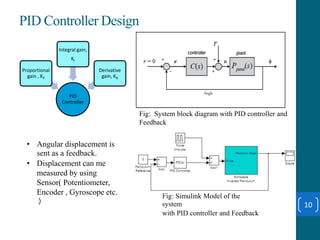
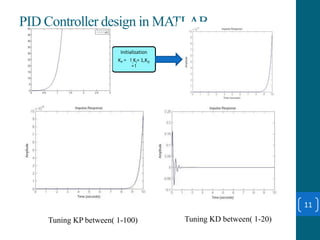
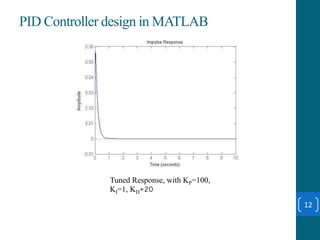
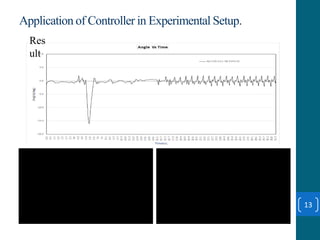
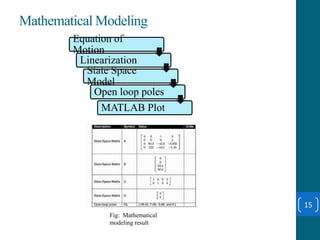
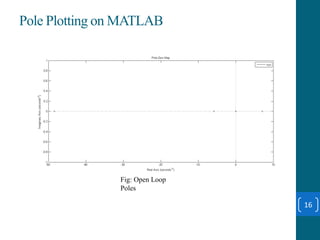
This document summarizes a student project on stabilizing and balancing linear and rotary inverted pendulum systems. It discusses the design and implementation of PID controllers to balance an inverted pendulum mounted on a cart (linear system) and a rotary inverted pendulum prototype. Key steps included mathematical modeling, simulation in MATLAB, PID controller tuning, and applying the controller to experimental setups. Results showed the systems could be stabilized using optimized PID and LQR controllers designed via pole placement and minimizing cost functions.

1. Stabilizing and balancing of
Linear and Rotary Inverted Pendulum system.
Presented by-
Nowab Md. Aminul Haq
Student ID. -1010130
Ashik-E-Rasul
Student ID. 1010132
Department of Mechanical Engineering
Bangladesh University of Engineering and Technology (BUET)
1
Supervised by-
Dr. Md. Zahurul Haq
Professor & Head.
Department of Mechanical Engineering, BUET.

2. What is an Inverted Pendulum ?
2
A Pendulum that has its center of mass above its pivot
point.
• Inherently unstable.
• Must be actively balanced in order to
remain upright.
• Must have a feedback system to keep
it balanced.
Criteria for Balancing
• Moving the Pivot point .
• Applying torque at the Pivot
point.
• Generating a net torque on the
Pendulum.
• Vertically Oscillating the Pivot
point.

3. Real life Examples
3

4. Types of Inverted Pendulum
4
In general two types-
1. Linear Inverted Pendulum
2. Rotary Inverted Pendulum
Moving the pivot point
horizontally
Applying a torque at the
pivot point

5. Our Thesis Work
5
Inverted pendulum
pivoted on cart
Rotary Inverted pendulumSelf Balancing Vehicle prototype
Linear Inverted
Pendulum

6. Linear Inverted Pendulum
6

7. Methodology of work
7
Study of System dynamics
Mathematical Modeling
MATLAB Simulation
PID Controller design in MATLAB
Application of Controller in
Experimental Setup.

8. System Dynamics and Mathematical Modeling
8
• 2D problem, where the pendulum is constrained
to move in the vertical plane.
• Control input is the force , F that moves the cart
horizontally.
• Outputs are the angular position of the
pendulum and the horizontal position , of the
cart .
• Pendulum is vertically upright , when = pi
System Transfer Functions

9. MATLAB Simulation of the System.
9
Time
phi
• No Feedback, No Controller.
• The System goes without
bound.
• The pendulum falls down
within seconds.
Fig: System behavior without Feedback and
Controller.

10. PID Controller Design
10
Angle
Fig: Simulink Model of the
system
with PID controller and Feedback
Fig: System block diagram with PID controller and
Feedback
PID
Controller
Proportional
gain , KP
Integral gain,
KI
Derivative
gain, KD
• Angular displacement is
sent as a feedback.
• Displacement can me
measured by using
Sensor( Potentiometer,
Encoder , Gyroscope etc.
)

11. PID Controller design in MATLAB
11
Initialization
KP = 1,KI= 1,KD
=1
Tuning KP between( 1-100) Tuning KD between( 1-20)

12. 12
PID Controller design in MATLAB
Tuned Response, with KP=100,
KI=1, KD=20

13. Application of Controller in Experimental Setup.
13
Res
ult

14. Rotary Inverted Pendulum
14
Fig: ExperimentalFig: Rotary Inverted Pendulum

15. Mathematical Modeling
15
Equation of
Motion
Linearization
State Space
Model
Open loop poles
MATLAB Plot
Fig: Mathematical
modeling result

16. Pole Plotting on MATLAB
16
Fig: Open Loop
Poles

17. Controller Design(Pole Placement Method)
17
Controll
ability
Desired
Poles
• ζ = 0.7.
• ωn = 4 rad/s
• |α| < 15 deg.
•
Gain
Calculat
ion
• To move the poles to desired location
Simulati
on
• Simulate The result
To
Model
• Apply on the system
2
. . . ]
( )
[ n
Ran
T B
k
AB A B A B
T n


3 430, 40p p   

18. Simulink Model
18

19. Simulation Result
19

20. Implementation on Model
20

21. Poles and Stability
21

22. Designing an optimal controller
22
Linear Quadratic Regulator(LQR)
Cost
Function
Design
Matrices
• Design Matrices(Q and R) with trial and error
• Control effort(Vm) is limited
Gain
• Calculate Controller Gain Using MATLAB
Simulation
• Done in Simulink
To Model
• Apply on the Model

23. Simulation Results
23

24. 24
Simulation Results

25. 25
Simulation Results

26. 26
Motor Voltage

27. 27
PendulumAngle

28. 28
ArmAngle

29. 29
Concluding Remarks
• Experiment study of Linear Inverted Pendulum, considering both
the Pendulum Angle and cart position.
• Balancing can be studied with other modern controllers, ex.
Fuzzy Controller, Neural Network etc.
• A comperative study of different controllers can also be done, to
analyze which controller provides the best Balancing.

30. Thank you!!
30