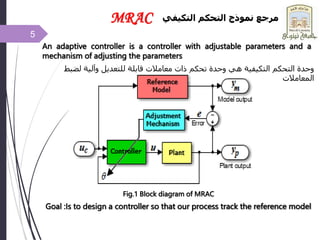
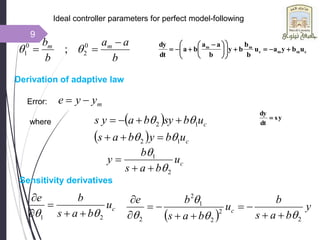
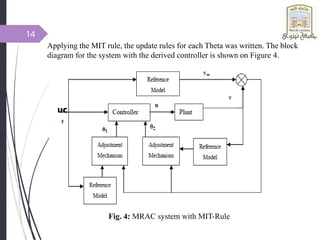
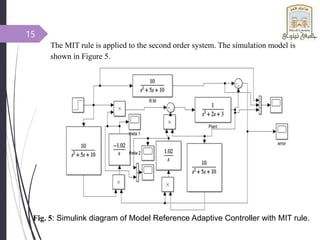
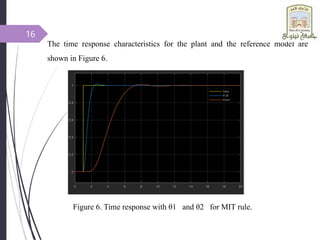
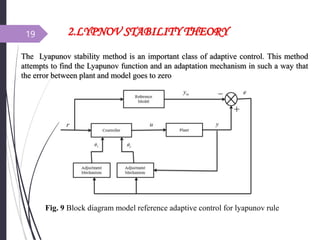
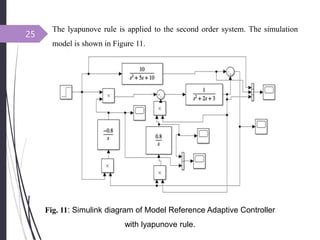
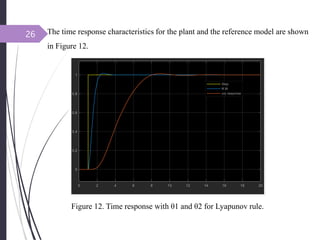
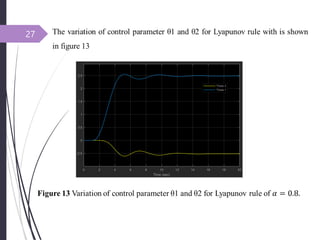
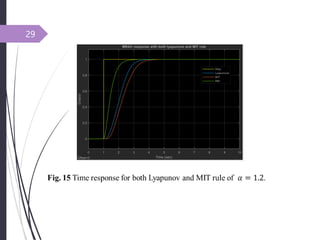
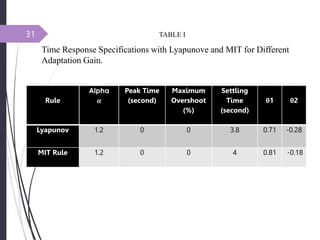
This document introduces adaptive control and model reference adaptive control (MRAC). It discusses two methods for parameter adaptation in MRAC - the MIT rule and Lyapunov stability theory. The MIT rule uses a gradient descent approach to minimize the error between the plant and reference model. Lyapunov stability theory finds a Lyapunov function and adaptation mechanism to drive the error to zero. Examples are provided to illustrate applying each method to an adaptive controller for a second order system. Simulation results show the plant output tracking the reference model in both cases.

1. INTRODUCTION TO ADAPTIVE
CONTROL
BY
Mohammed Nawfal Sheet
Hussien Hani Nayef
Muhammad Yasir Adel
Supervised by
Abdullah I. Abdullah
Ali K. Mahmoud
1

2. Contents
 Adaptive Control
 Why Adaptive Control ?
 MRAC
 MIT Rule
 Design Example
 Lyapunove Rule
 Design example
2

3. 3
Adaptive Control
Adaptive control is the control method used by a controller which must adapt to
a controlled system with parameters which vary, or are initially uncertain. For
example, as an aircraft flies, its mass will slowly decrease as a result of fuel
consumption.
Classification of adaptive control techniques
1.Direct Method:
2.Indirect Method:
3.Hybrid method
Estimate the controller parameters
Estimate the system parameters
‫هي‬
‫طريقة‬
‫التحكم‬
‫المستخدمة‬
‫من‬
‫قبل‬
‫المسيطرة‬
‫والتي‬
‫يجب‬
‫أن‬
‫تتكيف‬
‫لنظام‬
‫متغ‬
‫ير‬
‫المعامالت‬
‫أو‬
‫غير‬
‫مؤكدة‬
‫في‬
‫البداية‬
.
‫على‬
‫سبيل‬
‫المثال‬
،
‫عندما‬
‫تطير‬
‫طائرة‬
‫ستنخفض‬
‫كتلتها‬
‫ببطء‬
‫نتيجة‬
‫الستهالك‬
‫الوقود‬
.
‫التكيفي‬ ‫التحكم‬

4. 4
2.System dynamics experience unpredictable parameter variations
as the control operation goes on
1.Systems to be controlled have parameter uncertainty
Why Adaptive Control ?
Examples
1.Robot manipulation
2.Ship steering
3.Aircraft control
1
.
‫متغيرة‬ ‫معامالت‬ ‫لديها‬ ‫عليها‬ ‫السيطرة‬ ‫يجب‬ ‫التي‬ ‫النظم‬
2
.
‫يمك‬ ‫ال‬ ‫التي‬ ‫المعامالت‬ ‫لتغيرات‬ ‫تتغير‬ ‫النظام‬ ‫استجابة‬
‫التنبؤ‬ ‫ن‬
‫التحكم‬ ‫عملية‬ ‫الستمرار‬ ‫بها‬
‫التكيفي‬ ‫التحكم‬ ‫لماذا‬

5. 5
Fig.1 Block diagram of MRAC
Goal :Is to design a controller so that our process track the reference model
An adaptive controller is a controller with adjustable parameters and a
mechanism of adjusting the parameters
MRAC
‫لض‬ ‫وآلية‬ ‫للتعديل‬ ‫قابلة‬ ‫معامالت‬ ‫ذات‬ ‫تحكم‬ ‫وحدة‬ ‫هي‬ ‫التكيفية‬ ‫التحكم‬ ‫وحدة‬
‫بط‬
‫المعامالت‬
‫التكيفي‬ ‫التحكم‬ ‫نموذج‬ ‫مرجع‬

6. 6
Adjustment of system parameters in a MRAC can be
obtained in two ways.
GRADIENT METHOD (MIT RULE)
LYPNOV STABILITY THEORY
MRAC IS COMPOSED OF
 Plant containing unknown parameters
 Reference model
 Adjustable parameters containing control law
 Ordinary feed back loop

7. m
y
y
e 

Tracking error:
Introduce the cost function J:   2
2
1
e
J 

Where θ is a vector of controller parameters. Change the parameters in the
direction of the negative gradient of e2.
7
Fig.2 :
1.MIT RULE

8. 












e
e
J
dt
d


e is called the sensitivity derivative. It indicates how the error is
influenced by the adjustable parameters θ.
Example 1:
Process: bu
y
a
dt
dy



Model: c
m
m
m
m
u
b
y
a
dt
dy



Controller: y
u
u c 2
1 
 

Closed loop system:
    c
c u
b
y
b
a
y
u
b
ay
bu
y
a
dt
dy
1
2
2
1 


 










Define the MIT Rule
8

9. Ideal controller parameters for perfect model-following
b
a
a
b
b m
m 

 0
2
0
1 ; 

Derivation of adaptive law
Error: m
y
y
e 

where
c
u
b
a
s
b
y
2
1





 
  c
c
u
b
y
b
a
s
u
b
sy
b
a
y
s
1
2
1
2











Sensitivity derivatives
c
u
b
a
s
b
e
2
1 
 




 
y
b
a
s
b
u
b
a
s
b
e
c
2
2
2
1
2
2 


 









c
m
m
c
m
m
u
b
y
a
u
b
b
b
y
b
a
a
b
a
dt
dy

















 



y
s
dt
dy

9

10. Approximate    
m
a
s
b
a
s 


 2

where
e
u
a
s
a
s
e
u
a
s
b
t
c
m
m
c
m














 















 



1
1
e
y
a
s
a
s
e
y
a
s
b
t m
m
m






























 



2
2
m
a
b




10

11. 11
Fig.3

12. 12
Example 2:
Let the second order system be described by

13. 13

14. 14
Applying the MIT rule, the update rules for each Theta was written. The block
diagram for the system with the derived controller is shown on Figure 4.
Fig. 4: MRAC system with MIT-Rule
uc

15. 15
The MIT rule is applied to the second order system. The simulation model is
shown in Figure 5.
Fig. 5: Simulink diagram of Model Reference Adaptive Controller with MIT rule.

16. 16
The time response characteristics for the plant and the reference model are
shown in Figure 6.
Figure 6. Time response with θ1 and θ2 for MIT rule.

17. 17

18. 18
Fig. 8. Output error (y-ym) for MIT

19. 19 2.LYPNOV STABILITY THEORY
The Lyapunov stability method is an important class of adaptive control. This method
attempts to find the Lyapunov function and an adaptation mechanism in such a way that
the error between plant and model goes to zero
Fig. 9 Block diagram model reference adaptive control for lyapunov rule

20. 20 Considering, 2nd order Reference Model
And a 2nd order Plant Model:
By subtracting the equation (1) from equation (2), we get,

21. 21 Replacing in equation (5) from equation (3), we get, u
Integrating equation (9) with respect to t, we get,

22. 22
Let the Lyapunov function for the error dynamics,
This function is zero when e is zero and the controller parameters are equal to the correct
values.
For a valid Lyapunov function, time derivative of lyapunov function must be negative.
The derivative is given by e

23. 23

24. 24
Fig.10 Structure Diagram of MRAC for Lyapunov Rule.
r

25. 25
The lyapunove rule is applied to the second order system. The simulation
model is shown in Figure 11.
Fig. 11: Simulink diagram of Model Reference Adaptive Controller
with lyapunove rule.

26. 26 The time response characteristics for the plant and the reference model are shown
in Figure 12.
Figure 12. Time response with θ1 and θ2 for Lyapunov rule.

27. 27

28. 28
Fig. 14 Output error (y-ym) for Lyapunov rule

29. 29

30. 30
Fig. 16 Output error (y-ym) for MIT and Lyapunov rule

31. 31
Rule
Peak Time
(second)
Maximum
Overshoot
(%)
Settling
Time
(second)
θ1 θ2
Lyapunov 1.2 0 0 3.8 0.71 -0.28
MIT Rule 1.2 0 0 4 0.81 -0.18
TABLE I
Time Response Specifications with Lyapunove and MIT for Different
Adaptation Gain.