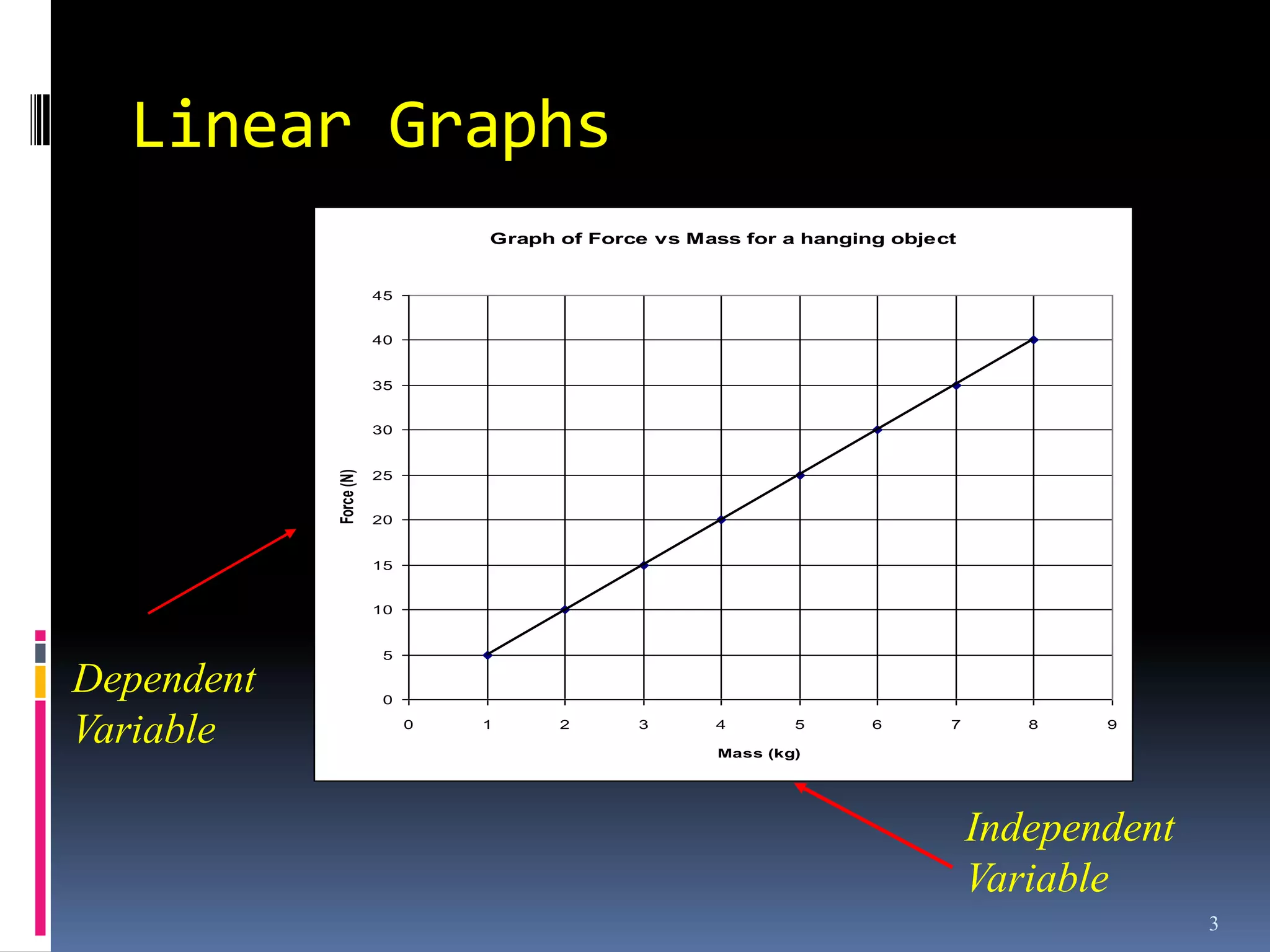
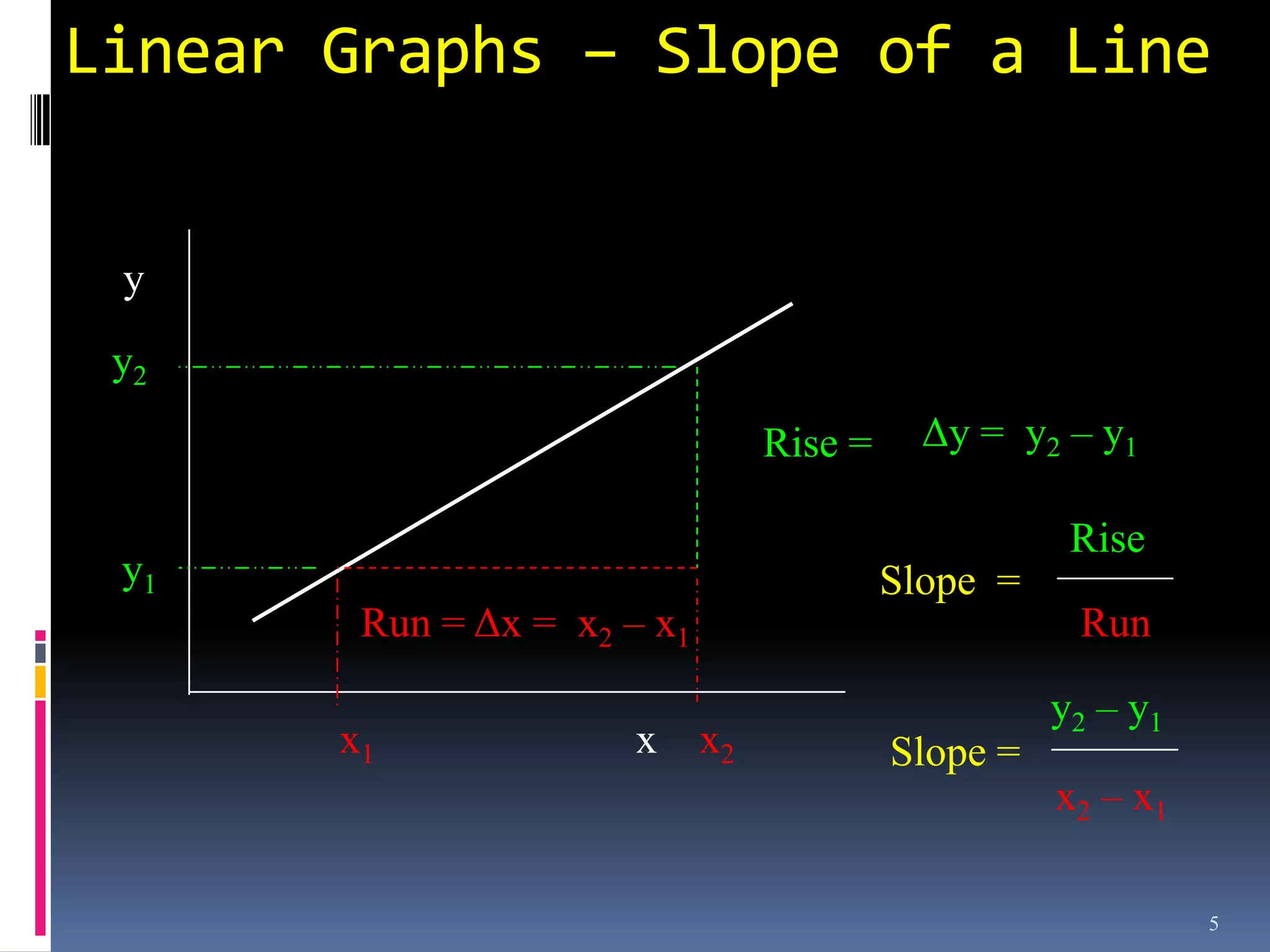
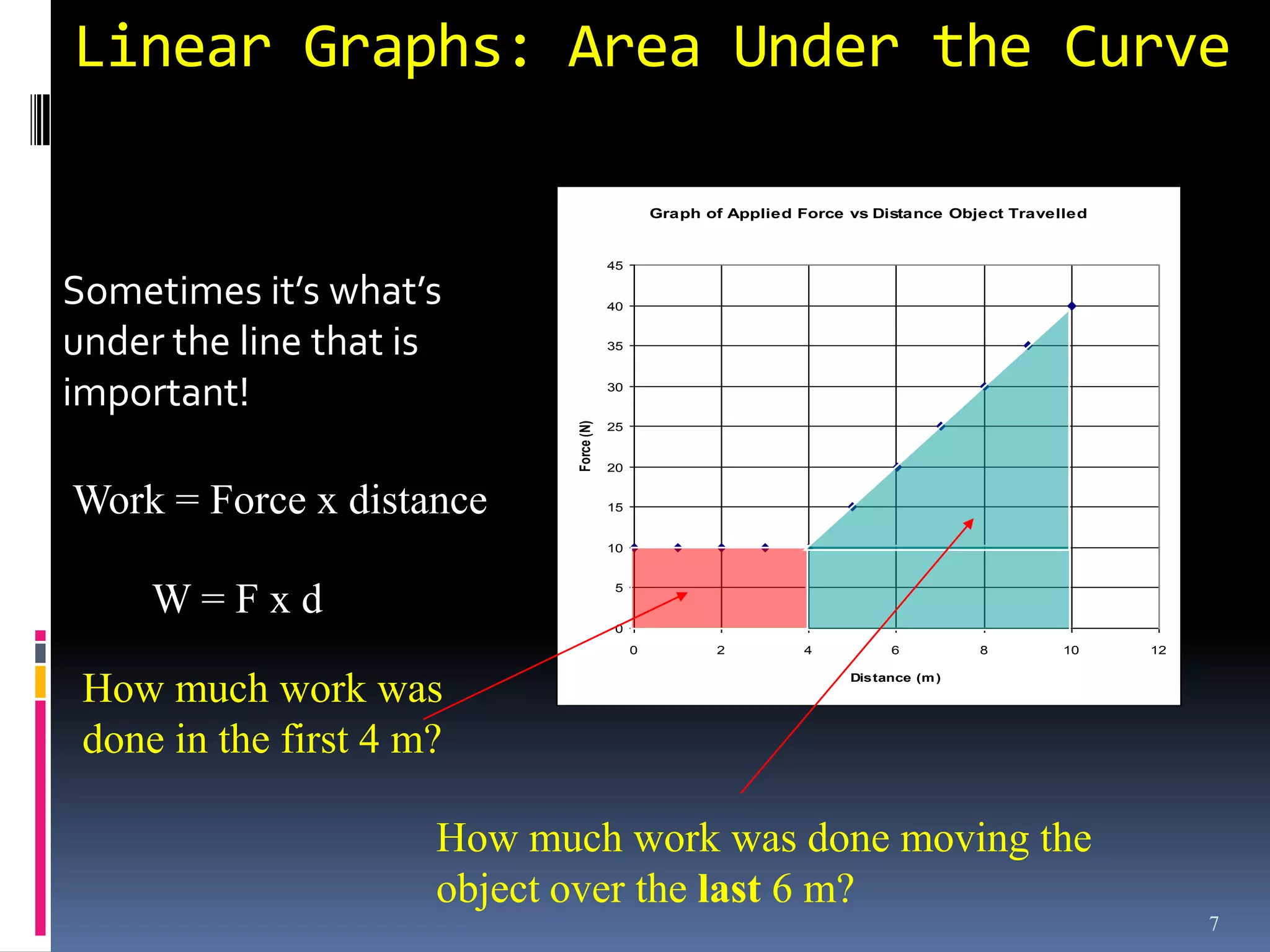
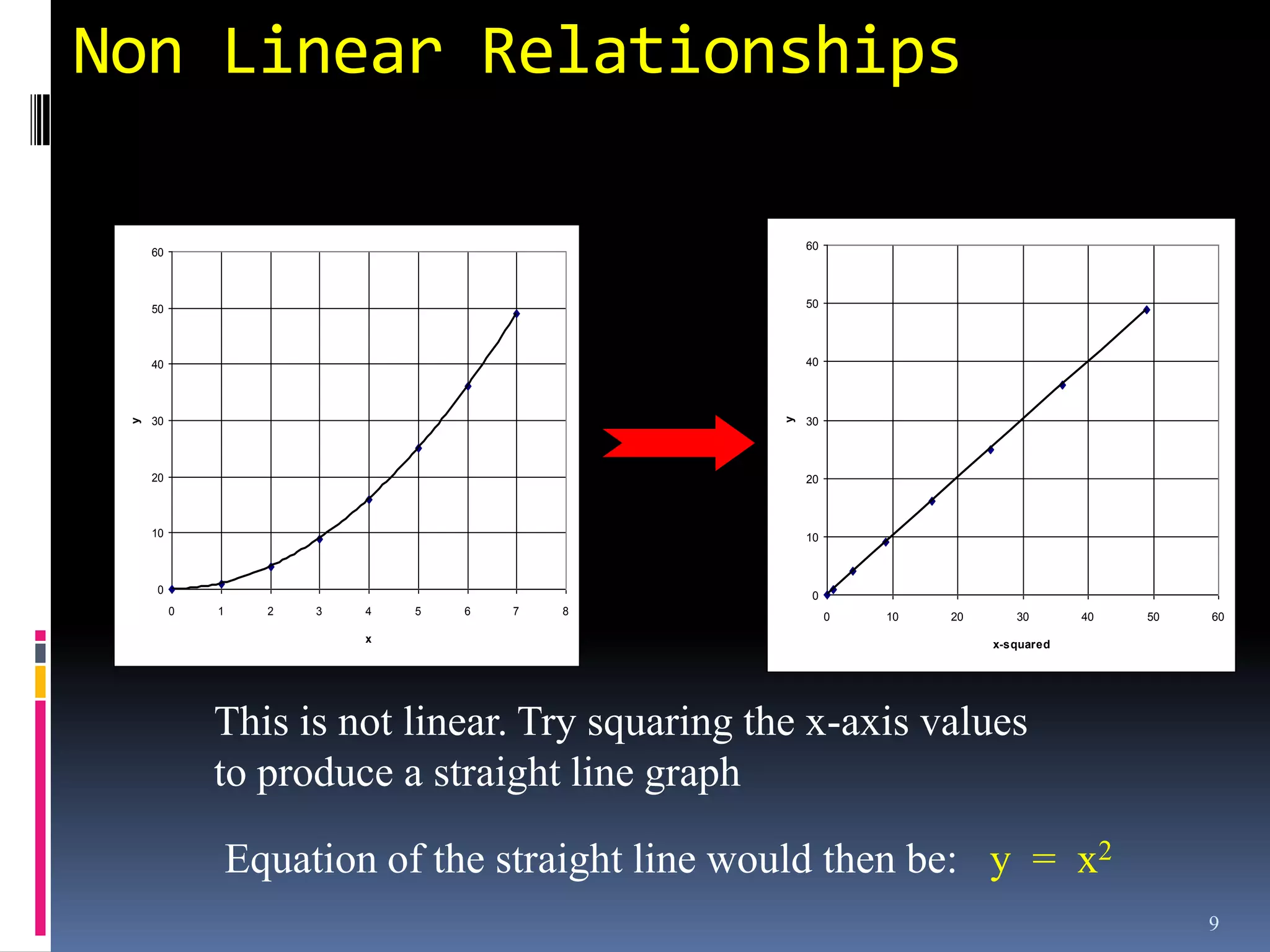
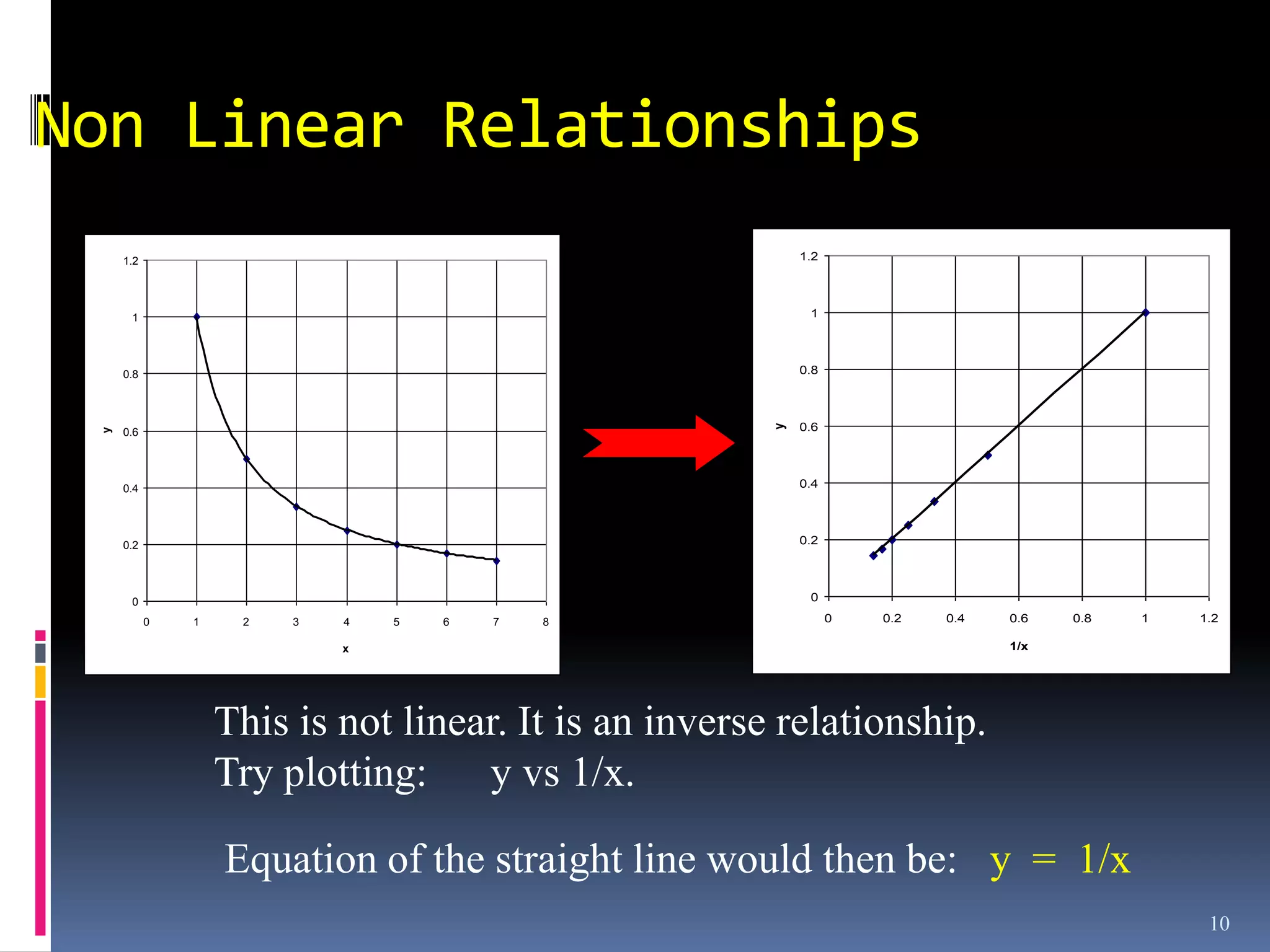
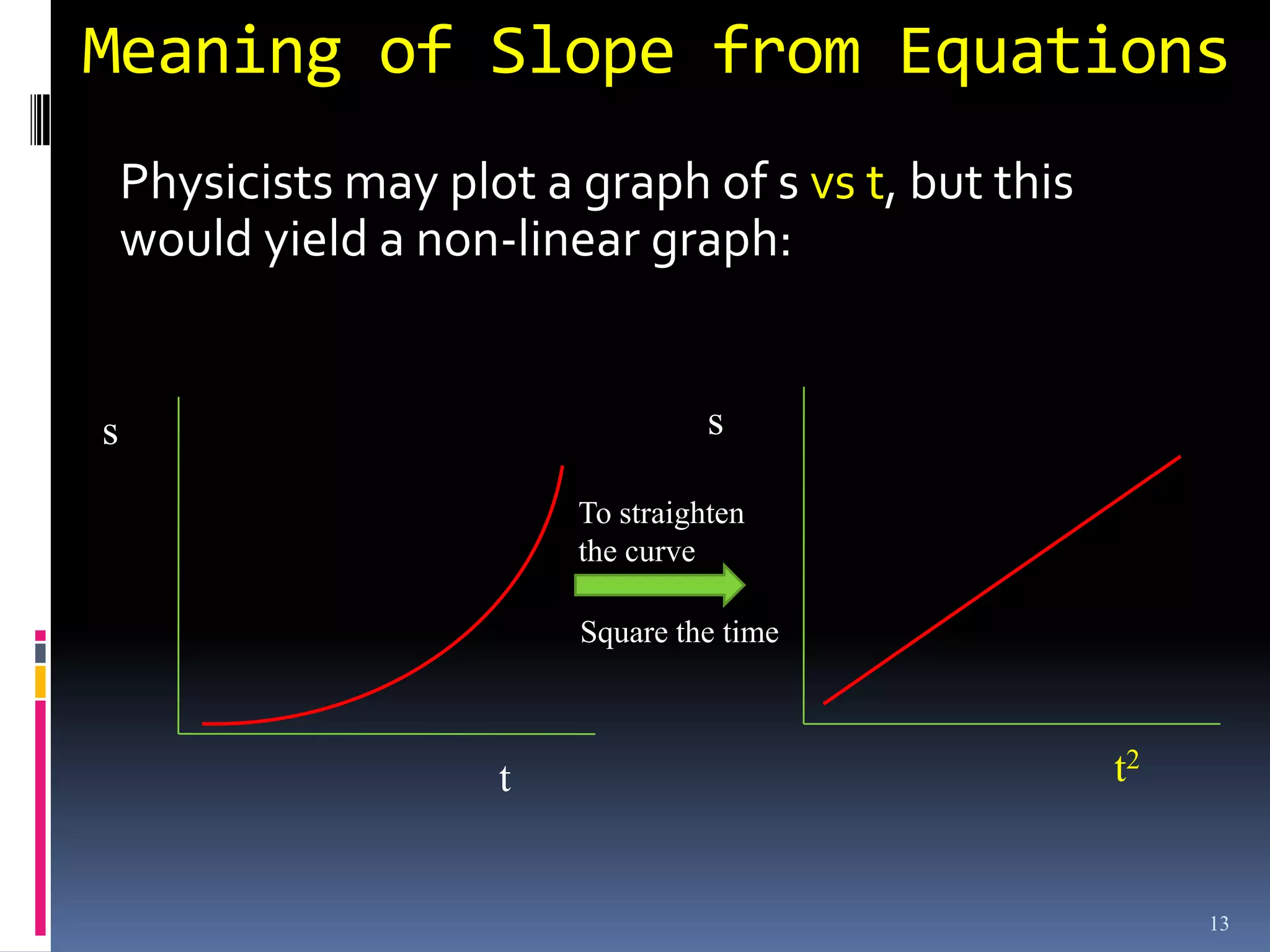
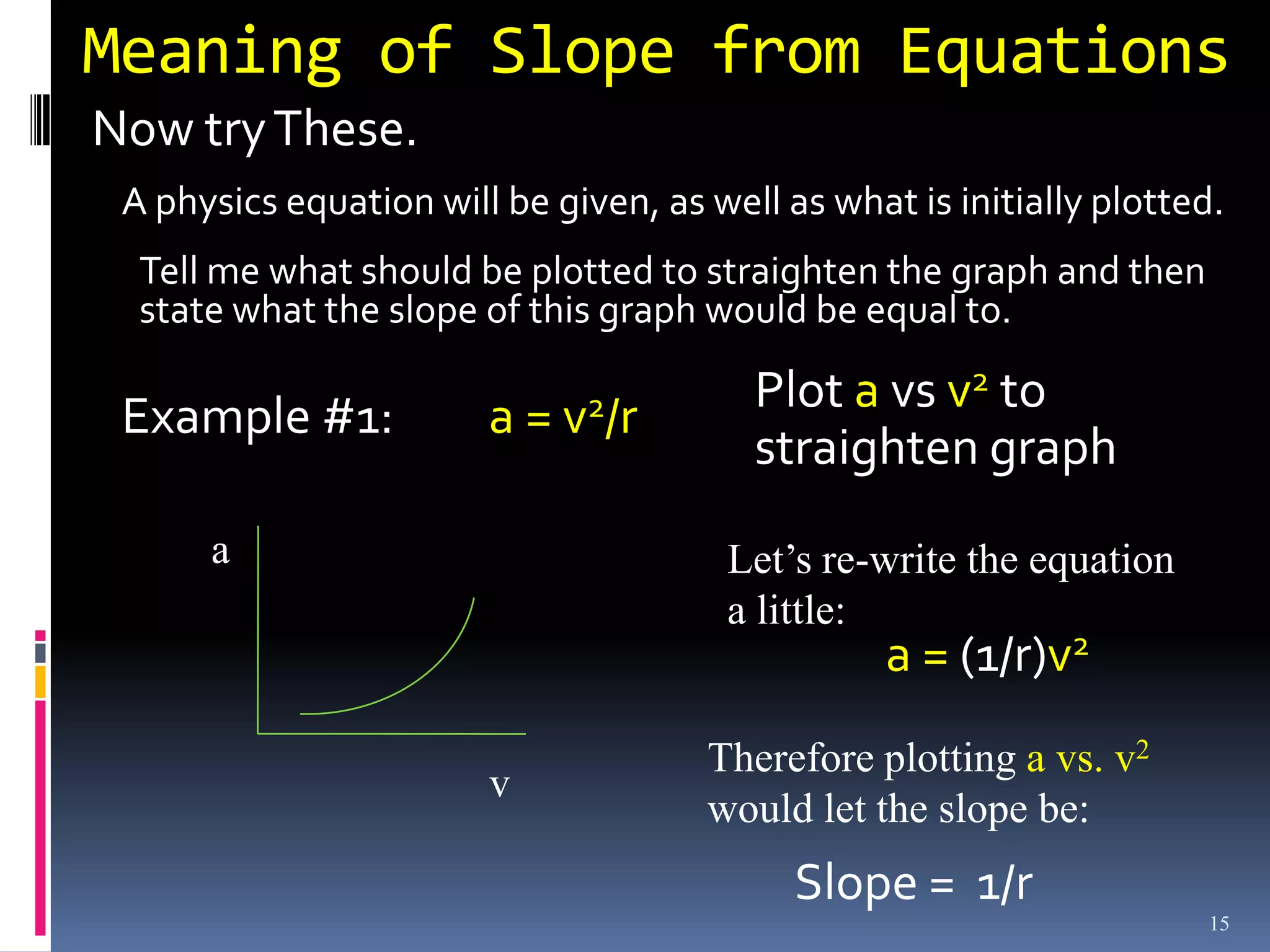
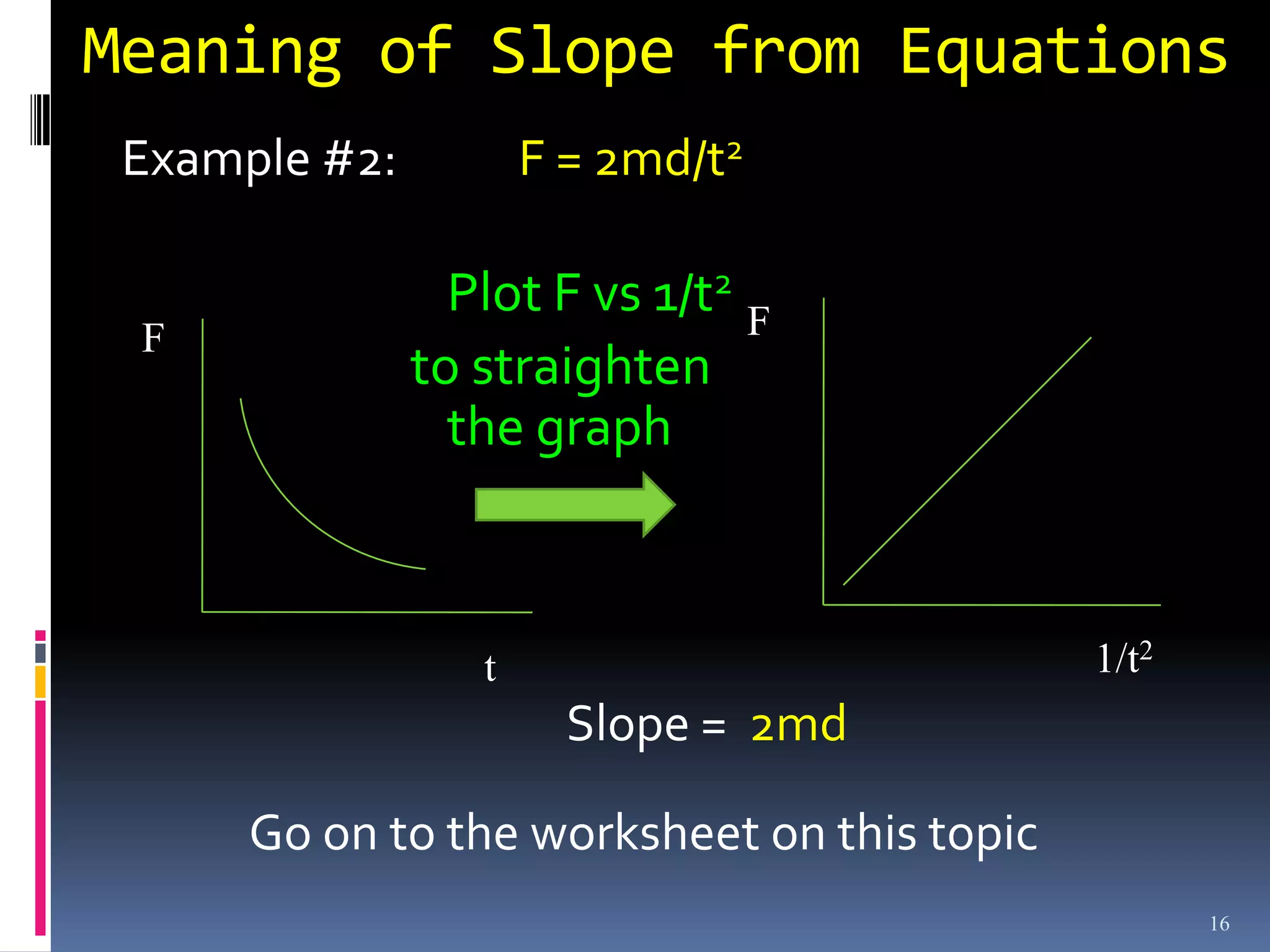
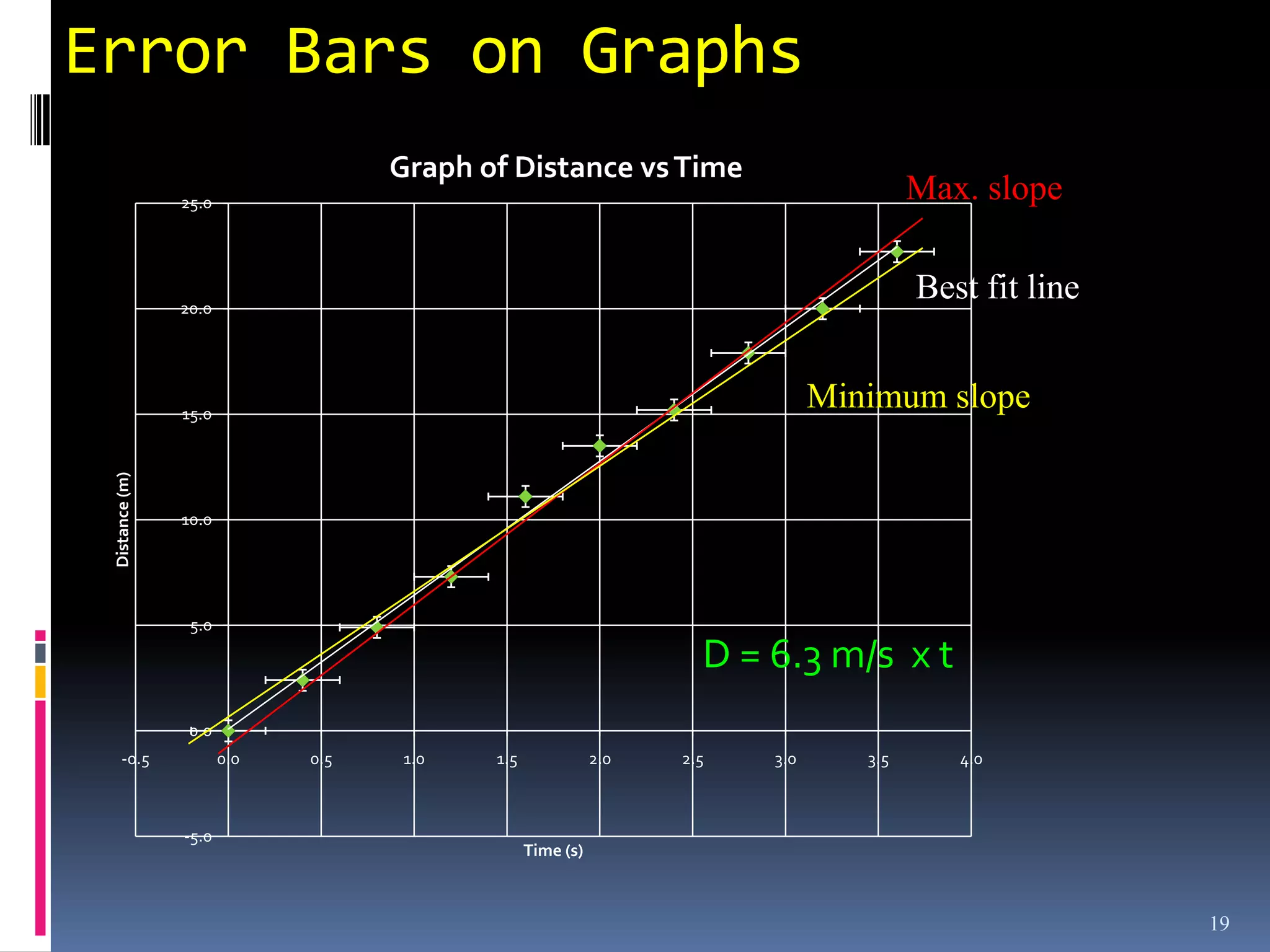
Graphs are used in physics to show relationships between variables. A linear graph indicates a direct proportional relationship between variables. The slope of a linear graph is calculated by taking the rise over the run and represents the ratio of change in the dependent variable to the change in the independent variable. For nonlinear relationships, manipulating the variables, such as squaring or taking reciprocals, can linearize the relationship. The slope of the resulting linear graph then represents a physical quantity defined by the original equation.

1. GRAPHS IN PHYSICS
1

2. Linear Graphs
Graphing data shows if a relationship exists
between two quantities also called variables.
If two variables show a linear relationship they
are directly proportional to each other.
Examine the following graph:
2

3. Linear Graphs
Graph of Force vs Mass for a hanging object
45
40
35
30
Force (N)
25
20
15
10
5
Dependent 0
Variable 0 1 2 3 4 5
Mass (kg)
6 7 8 9
Independent
Variable
3

4. Linear Graphs – Slope of a Line
The slope of a line is a ratio between the
change in the y-value and the change in
the x- value.
This ratio tells whether the two quantities
are related mathematically.
Calculating the slope of a line is easy!
4

5. Linear Graphs – Slope of a Line
y
y2
Rise = Δy = y2 – y1
Rise
y1 Slope =
Run = Δx = x2 – x1 Run
y2 – y1
x1 x x2 Slope =
x2 – x1
5

6. Linear Graphs – Equation of a Line
Once you know the slope then the equation of a line is very easily
determined.
Slope Intercept form for any line:
y = mx + b
y-intercept
slope (the value of y when x =0)
Of course in Physics we don’t use “x” & “y”. We could use F
and m, or d and t, or F and x etc.)
6

7. Linear Graphs: Area Under the Curve
Graph of Applied Force vs Distance Object Travelled
45
Sometimes it’s what’s 40
under the line that is 35
important! 30
Force (N)
25
20
Work = Force x distance 15
10
W=Fxd 5
0
0 2 4 6 8 10 12
How much work was Distance (m )
done in the first 4 m?
How much work was done moving the
object over the last 6 m?
7

8. Non Linear Relationships
 Not all relationships between variables are linear.
 Some are curves which show a squared or square
root relationship
In this course we use simple techniques to
“straighten the curve” into linear relationship.
8

9. Non Linear Relationships
60
60
50 50
40 40
y
30 30
y
20 20
10 10
0 0
0 1 2 3 4 5 6 7 8 0 10 20 30 40 50 60
x x-squared
This is not linear. Try squaring the x-axis values
to produce a straight line graph
Equation of the straight line would then be: y = x2
9

10. Non Linear Relationships
1.2 1.2
1 1
0.8 0.8
0.6
y
y
0.6
0.4 0.4
0.2 0.2
0 0
0 1 2 3 4 5 6 7 8 0 0.2 0.4 0.6 0.8 1 1.2
x 1/x
This is not linear. It is an inverse relationship.
Try plotting: y vs 1/x.
Equation of the straight line would then be: y = 1/x
10

11. Meaning of Slope from Equations
Often in Physics graphs are plotted and the
calculation of and the meaning of the slope
becomes an important factor.
We will use the slope intercept form
of the linear equation described
earlier.
y = mx + b
11

12. Meaning of Slope from Equations
Unfortunately physicists do not use the same
variables as mathematicians!
For example: s = ½xa x t
2
is a very common kinematic equation.
where s = distance, a = acceleration and t = time
12

13. Meaning of Slope from Equations
Physicists may plot a graph of s vs t, but this
would yield a non-linear graph:
s s
To straighten
the curve
Square the time
t t2
13

14. Meaning of Slope from Equations
But what would the slope of a d vs t2 graph represent?
Let’s look at the equation again:
s = ½at2 {s is plotted vs t2}
y = mx + b
What is left over must be equal to the slope of the line!
slope = ½ x a {and do not forget
about units: ms-2}
14

15. Meaning of Slope from Equations
Now try These.
A physics equation will be given, as well as what is initially plotted.
Tell me what should be plotted to straighten the graph and then
state what the slope of this graph would be equal to.
Example #1: a = v2/r Plot a vs v2 to
straighten graph
a Let’s re-write the equation
a little:
a = (1/r)v2
Therefore plotting a vs. v2
v
would let the slope be:
Slope = 1/r
15

16. Meaning of Slope from Equations
Example #2: F = 2md/t2
Plot F vs 1/t2 F
F
to straighten
the graph
t 1/t2
Slope = 2md
Go on to the worksheet on this topic
16

17. Error Bars on Graphs
You already know about including errors with all
measured values.
These errors must be included in any graph that is
created using these measured value. The errors are
shown as bars both in the horizontal and vertical
direction.
For example:
2.3 + 0.2 (horizontal ) 15.7 + 0.5 (vertical)
This would be shown
like this on the graph. Error Bars!
17

18. Error Bars on Graphs
Plot the following data and add in
the error bars:
time (s) Distance (m)
(+0.2) (+0.5)
0.0 0.0
0.4 2.4
0.8 4.9
1.2 7.3
1.6 11.1
2.0 13.5
2.4 15.2
2.8 17.9
3.2 20.0
3.6 22.7
18

19. Error Bars on Graphs
Graph of Distance vs Time
25.0
Max. slope
20.0
Best fit line
15.0
Minimum slope
Distance (m)
10.0
5.0
D = 6.3 m/s x t
0.0
-0.5 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
-5.0
Time (s)
19