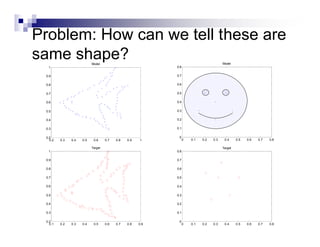
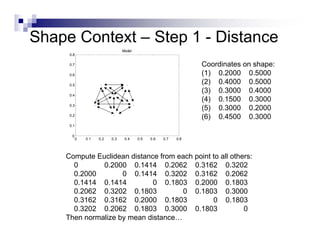
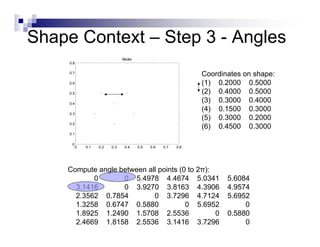
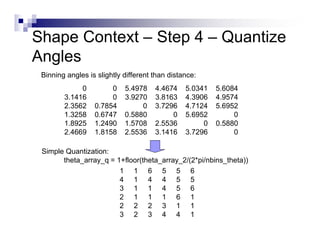
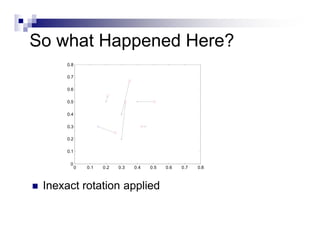
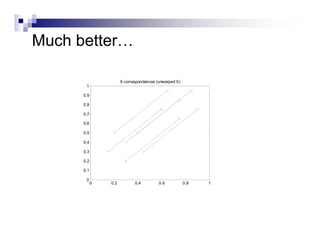
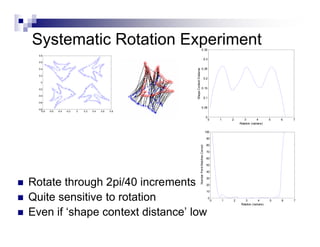
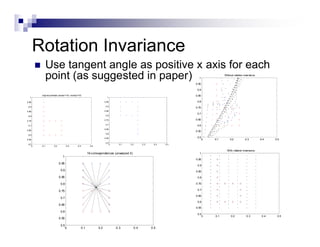
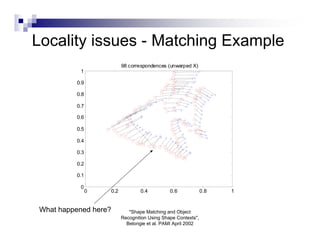
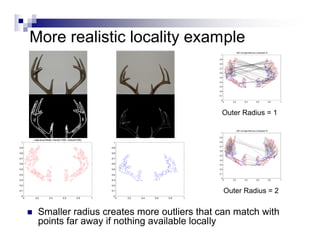
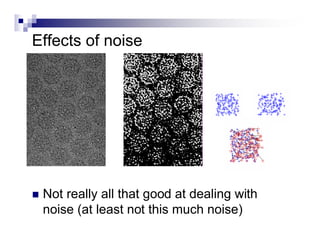
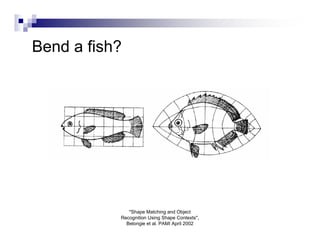
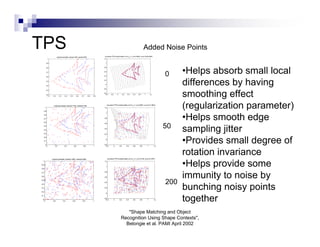
This document summarizes the shape context algorithm for shape matching and object recognition. It discusses computing shape contexts, which describe the distribution of relative positions of points around a shape. Shape contexts are represented as histograms of distances and angles between points. The algorithm finds correspondences between points on two shapes by matching their shape contexts and minimizing the total cost. Additional cost terms can be added, such as color or texture differences. The algorithm is shown to be robust to noise and inexact rotations.

1. Shape Contexts
Newton Petersen
4/25/2008
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

2. Agenda
 Study Matlab code for computing shape
context
 Look at limitations of descriptor
 Explore effect of noise
 Explore rotation invariance
 Explore effect of locality
 Explore Thin Plate Spline
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

3. Problem: How can we tell these are
same shape? Model Model
1 0.8
0.9 0.7
0.8 0.6
0.7 0.5
0.6 0.4
0.5 0.3
0.4 0.2
0.3 0.1
0.2 0
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Target Target
1 0.8
0.9 0.7
0.8 0.6
0.7 0.5
0.6 0.4
0.5 0.3
0.4 0.2
0.3 0.1
0.2 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

4. Shape Context – Step 1 - Distance
Model
0.8
0.7 Coordinates on shape:
0.6 (1) 0.2000 0.5000
0.5
(2) 0.4000 0.5000
(3) 0.3000 0.4000
0.4
(4) 0.1500 0.3000
0.3
(5) 0.3000 0.2000
0.2
(6) 0.4500 0.3000
0.1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Compute Euclidean distance from each point to all others:
0 0.2000 0.1414 0.2062 0.3162 0.3202
0.2000 0 0.1414 0.3202 0.3162 0.2062
0.1414 0.1414 0 0.1803 0.2000 0.1803
0.2062 0.3202 0.1803 0 0.1803 0.3000
0.3162 0.3162 0.2000 0.1803 0 0.1803
0.3202 0.2062 0.1803 0.3000 0.1803 0
Then normalize by mean distance…

5. Shape Context – Step 2 – Bin
Distances
Normalized distances between each point:
0 1.0623 0.7511 1.0949 1.6796 1.7004
1.0623 0 0.7511 1.7004 1.6796 1.0949
0.7511 0.7511 0 0.9575 1.0623 0.9575
1.0949 1.7004 0.9575 0 0.9575 1.5934
1.6796 1.6796 1.0623 0.9575 0 0.9575
1.7004 1.0949 0.9575 1.5934 0.9575 0
Create log distance scale for normalized distances (closer = more discriminate):
0.1250 0.2500 0.5000 1.0000 2.0000
Create distance histogram: Iterate for each scale incrementing bins when dist <
1 0 0 0 0 0 5 1 2 1 1 1
0 1 0 0 0 0 1 5 2 1 1 1
0 0 1 0 0 0
0 0 0 1 0 0 … 2
1
2
1
5
2
2
5
1
2
2
1
0 0 0 0 1 0 1 1 1 2 5 2
0 0 0 0 0 1 1 1 2 1 2 5
Bottom Line: Bins with higher numbers describe points closer together

6. Shape Context – Step 3 - Angles
Model
0.8
0.7
Coordinates on shape:
0.6 (1) 0.2000 0.5000
0.5 (2) 0.4000 0.5000
0.4
(3) 0.3000 0.4000
(4) 0.1500 0.3000
0.3
(5) 0.3000 0.2000
0.2
(6) 0.4500 0.3000
0.1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Compute angle between all points (0 to 2π):
0 0 5.4978 4.4674 5.0341 5.6084
3.1416 0 3.9270 3.8163 4.3906 4.9574
2.3562 0.7854 0 3.7296 4.7124 5.6952
1.3258 0.6747 0.5880 0 5.6952 0
1.8925 1.2490 1.5708 2.5536 0 0.5880
2.4669 1.8158 2.5536 3.1416 3.7296 0

7. Shape Context – Step 4 – Quantize
Angles
Binning angles is slightly different than distance:
0 0 5.4978 4.4674 5.0341 5.6084
3.1416 0 3.9270 3.8163 4.3906 4.9574
2.3562 0.7854 0 3.7296 4.7124 5.6952
1.3258 0.6747 0.5880 0 5.6952 0
1.8925 1.2490 1.5708 2.5536 0 0.5880
2.4669 1.8158 2.5536 3.1416 3.7296 0
Simple Quantization:
theta_array_q = 1+floor(theta_array_2/(2*pi/nbins_theta))
1 1 6 5 5 6
4 1 4 4 5 5
3 1 1 4 5 6
2 1 1 1 6 1
2 2 2 3 1 1
3 2 3 4 4 1

8. Shape Context – Step 5 – Combine
 R and theta numbers are combined to one descriptor
(slightly tricky Matlab code)
 Captures number of points in each R, theta bin
 Effectively turned N points into
N*NumRadialBins*NumThetaBins = Rich Descriptor
100021000001000000000000100000
… for each point
… relative to each point and not a global origin

9. Matching – Cost Matrix
 Calculate ‘cost’ of matching each point to every
other point
 Cost of matching point i to point j = Chi-squared
similarity between row i and row j in shape
context descriptor
All histogram bins in Bin values normalized
one row by total number of points

10. Matching – Additional Cost Terms
 Easy to add in other terms
 For ‘real’ images, possible to add in other
measures of difference between point i
and j
 Surrounding Color Difference
 Surrounding Texture Difference
 Surrounding Brightness Difference
 Tangent Angle Difference
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

11. Matching
 Find pairing of points that leads to least total
cost
 Hungarian Method
 O(n^3)
Cost of matching point 1 of shape 1 to point 2 of
shape 2
a1 a2
b1 b2
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

12. So what Happened Here?
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
 Inexact rotation applied

13. Much better…
6 correspondences (unwarped X)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1

14. Systematic Rotation Experiment 0.35
0.8
0.3
0.6
0.4 0.25
Shape Context Distance
0.2
0.2
0
-0.2 0.15
-0.4
0.1
-0.6
0.05
-0.8
-0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8
0
0 1 2 3 4 5 6 7
Rotation (radians)
100
90
80
Number Point Matches Correct
70
60
50
40
Rotate through 2pi/40 increments
30
 20
10
 Quite sensitive to rotation 0
0 1 2 3 4
Rotation (radians)
5 6 7
 Even if ‘shape context distance’ low

15. Providing Rotation Invariance
 Relation between tangent angles stays the
same as points rotate
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

16. Rotation Invariance
 Use tangent angle as positive x axis for each
point (as suggested in paper) 1
Without rotation invariance
0.95
0.9
original pointsets (nsamp1=16, nsamp2=16) 0.85
1 1
0.95 0.95 0.8
0.9 0.9
0.75
0.85 0.85
0.7
0.8 0.8
0.75 0.75 0.65
0.7 0.6
0.7
0.65
0.65 0.55
0.6
0.6
0.55 0.5
0.55 0 0.1 0.2 0.3 0.4 0.5
0.5
0.5 0 0.1 0.2 0.3 0.4 0.5
0 0.1 0.2 0.3 0.4 0.5
With rotation invariance
16 correspondences (unwarped X) 1
1
0.95
0.95
0.9
0.9 0.85
0.85 0.8
0.8 0.75
0.75 0.7
0.65
0.7
0.6
0.65
0.55
0.6
0.5
0 0.1 0.2 0.3 0.4 0.5
0.55
0.5
0 0.1 0.2 0.3 0.4 0.5

17. Rotation Invariance
 Do you really want 6 and 9 matched?
 Depends on the shape…
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

18. Locality issues - Matching Example
98 correspondences (unwarped X)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
What happened here? "Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

19. What could produce ‘incorrect’
descriptors?
 As we just saw,
 Rotation that puts points in different relative bins
 Different numbers of points in different regions of
shapes
 Any important distinction that ends up in the same bin is
effectively lost
 Chance of happening increases with distance
 Conversely any nearby feature relation that is
unimportant is granted a distinction in the descriptor
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

20. More realistic locality example
250 correspondences (unwarped X)
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0 0.2 0.4 0.6 0.8 1
Outer Radius = 1
250 correspondences (unwarped X)
1
0.9
original pointsets (nsamp1=250, nsamp2=250)
1 1 0.8
0.7
0.9 0.9
0.6
0.8 0.8
0.5
0.7 0.7
0.4
0.6 0.6 0.3
0.5 0.5 0.2
0.1
0.4 0.4
0
0.3 0.3 0 0.2 0.4 0.6 0.8 1
0.2 0.2
0.1 0.1
Outer Radius = 2
0 0
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
 Smaller radius creates more outliers that can match with
points far away if nothing available locally

21. Effects of noise
 Not really all that good at dealing with
noise (at least not this much noise)

22. Thin Plate Spline Warping
 Meant to model transformations that
happen when bending metal
 Picks a warp that minimizes the ‘bending
energy’ above and minimizes shape
distance "Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

23. Bend a fish?
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

24. TPS original pointsets (nsamp1=98, nsamp2=98)
Added Noise Points
recovered TPS transformation (k=5,o=1, I=0.014625, error=0.0016206)
f
1 1.2
0.9 1
•Helps absorb small local
0.8 0.8
0
0.7 0.6
0.4
0.6
0.5
0.4
0.2
0
-0.2
differences by having
smoothing effect
0.3
-0.4
0.2 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.9
1
original pointsets (nsamp1=148, nsamp2=148)
1.2
recovered TPS transformation (k=5,o =1, I=0.36361, error=0.21063)
f
(regularization parameter)
•Helps smooth edge
1
0.8
0.7 0.8
0.6
50
0.6
sampling jitter
0.5
0.4
0.4
0.3 0.2
•Provides small degree of
0.2
0
0.1
0 -0.2
0 0.2 0.4 0.6 0.8 1 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
recovered TPS transformation (k=5, o=1, I=0.33138, error=0.3767)
rotation invariance
•Helps provide some
original pointsets (nsamp1=298, nsamp2=298) f
1 1.2
0.9
1
0.8
immunity to noise by
0.7 0.8
0.6 0.6
0.5
200
bunching noisy points
0.4
0.4
0.3 0.2
0.2
0
together
0.1
-0.2
0 -0.2 0 0.2 0.4 0.6 0.8 1 1.2
0 0.2 0.4 0.6 0.8 1
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

25. Conclusion
 Shape context => binning of spatial
relationships between points
 Good for ‘clean’ shapes
 Examples from paper => handwriting,
trademarks
 Struggles with clutter noise
 Thin Plate Spline helps quite a bit
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002

26. Discussion
 How does this compare to other descriptors?
 What would work better with Maysam’s viruses?
 Any ideas for making descriptor know what
geometrical relationships are most important?
(like active appearance models)
 Any ideas for improving runtime
"Shape Matching and Object
Recognition Using Shape Contexts",
Belongie et al. PAMI April 2002