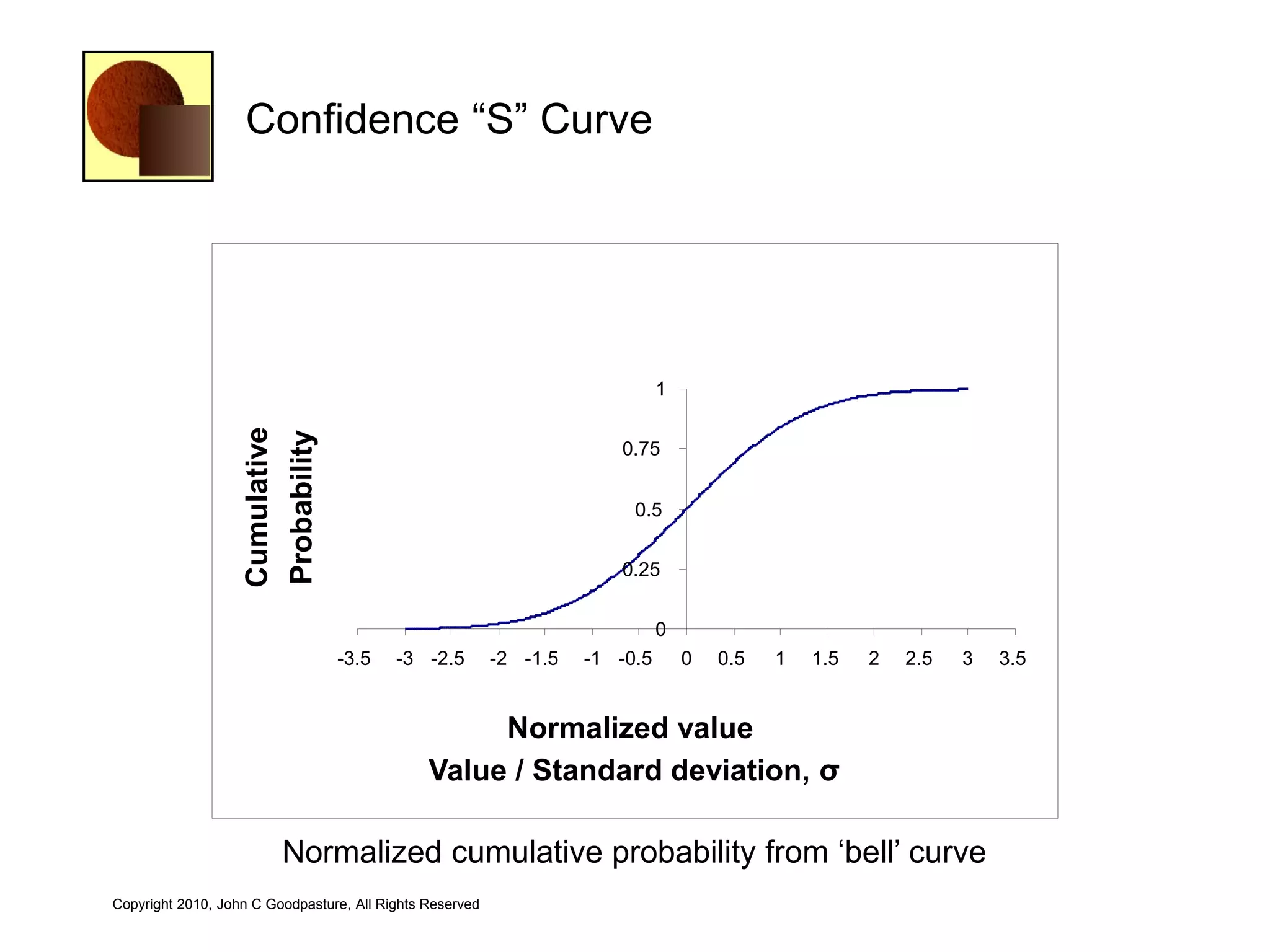
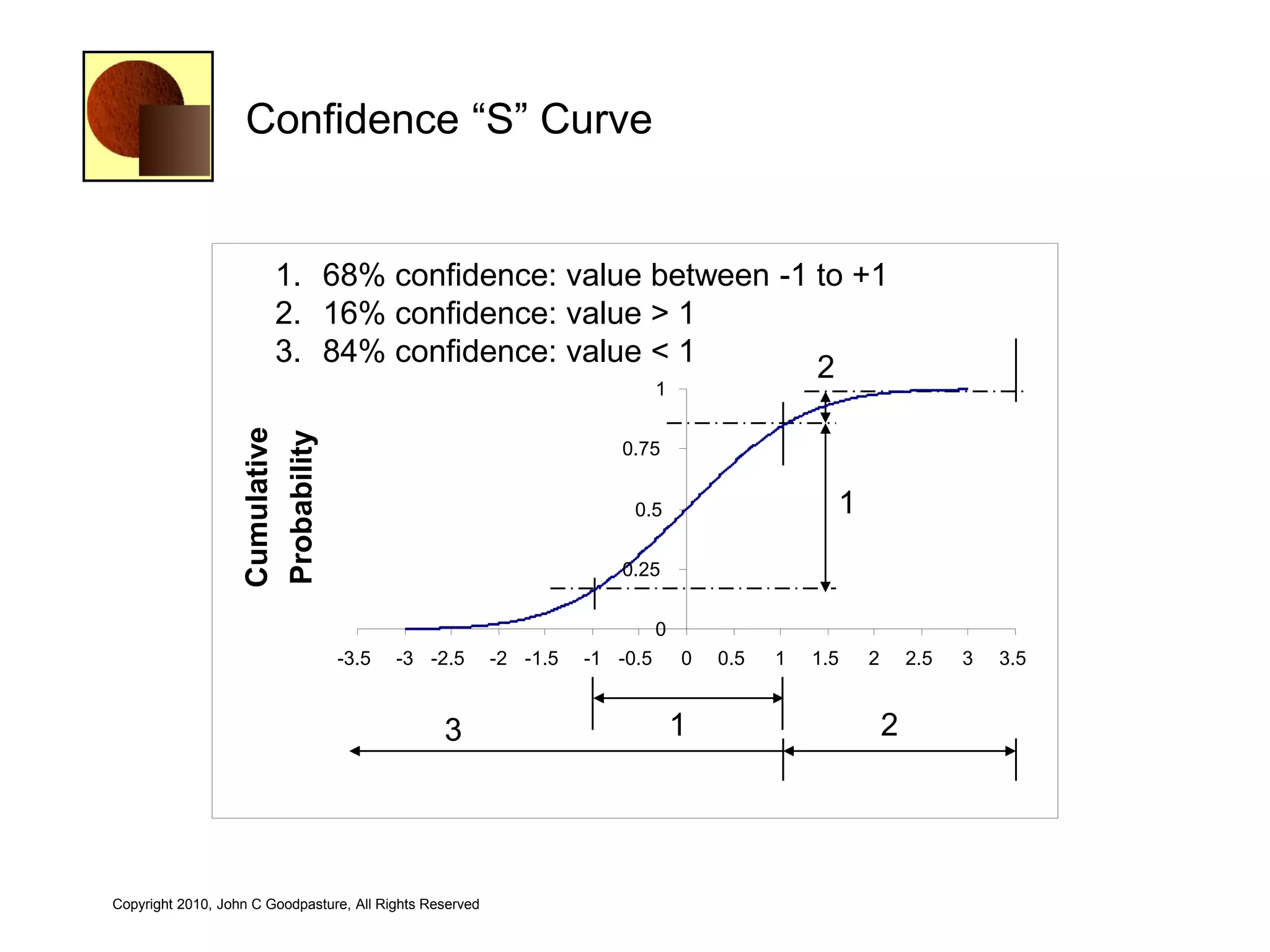
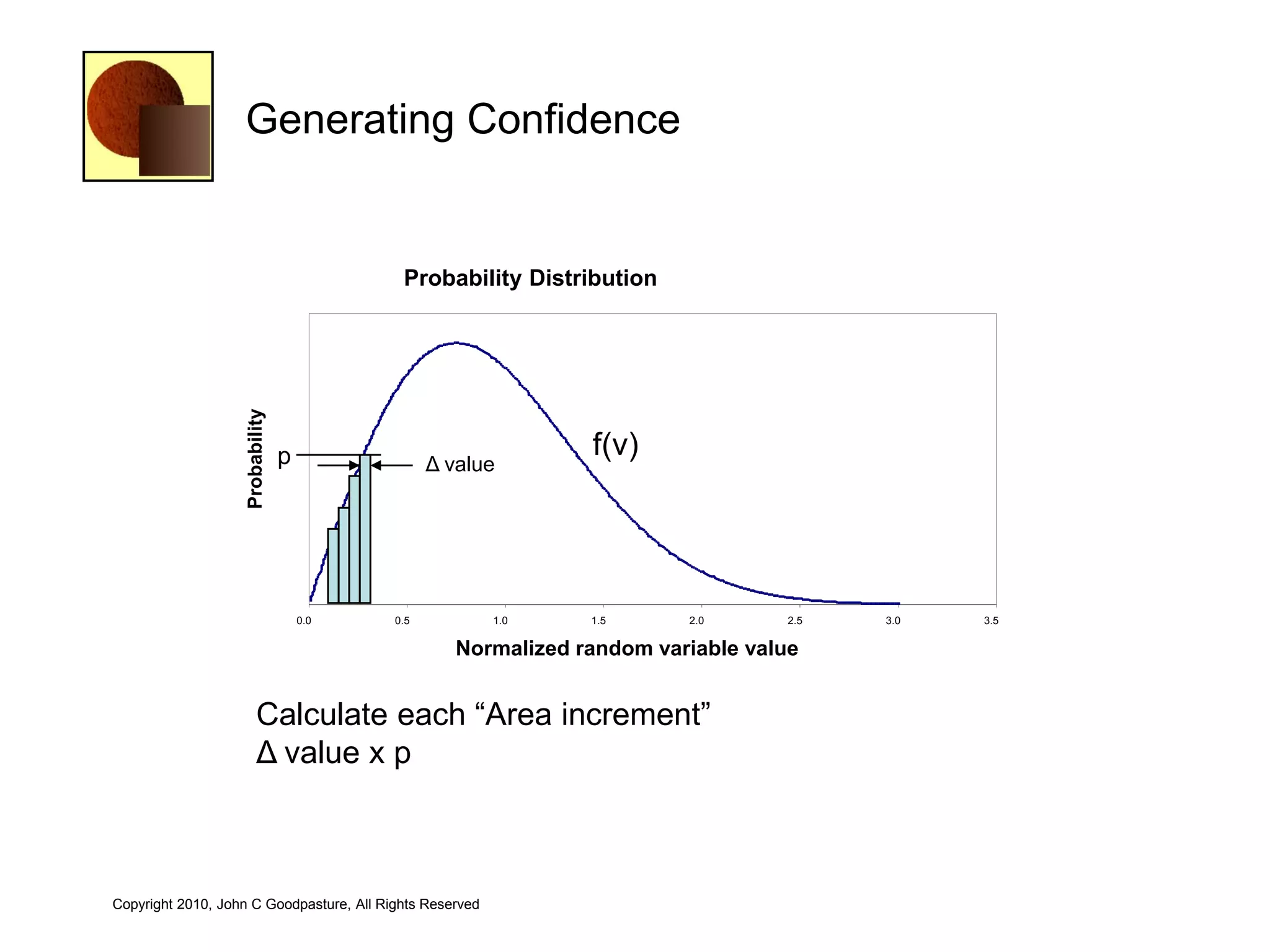
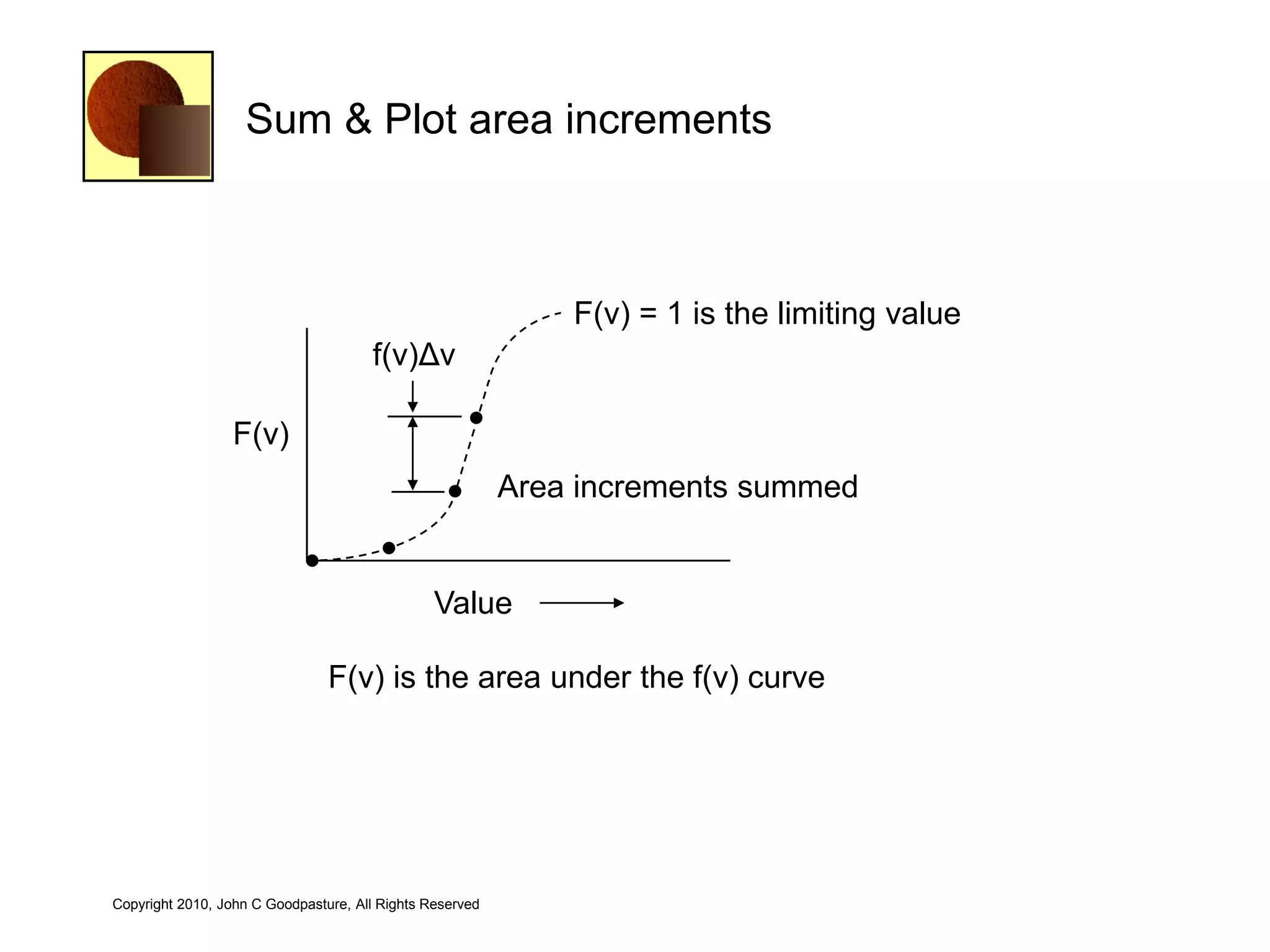
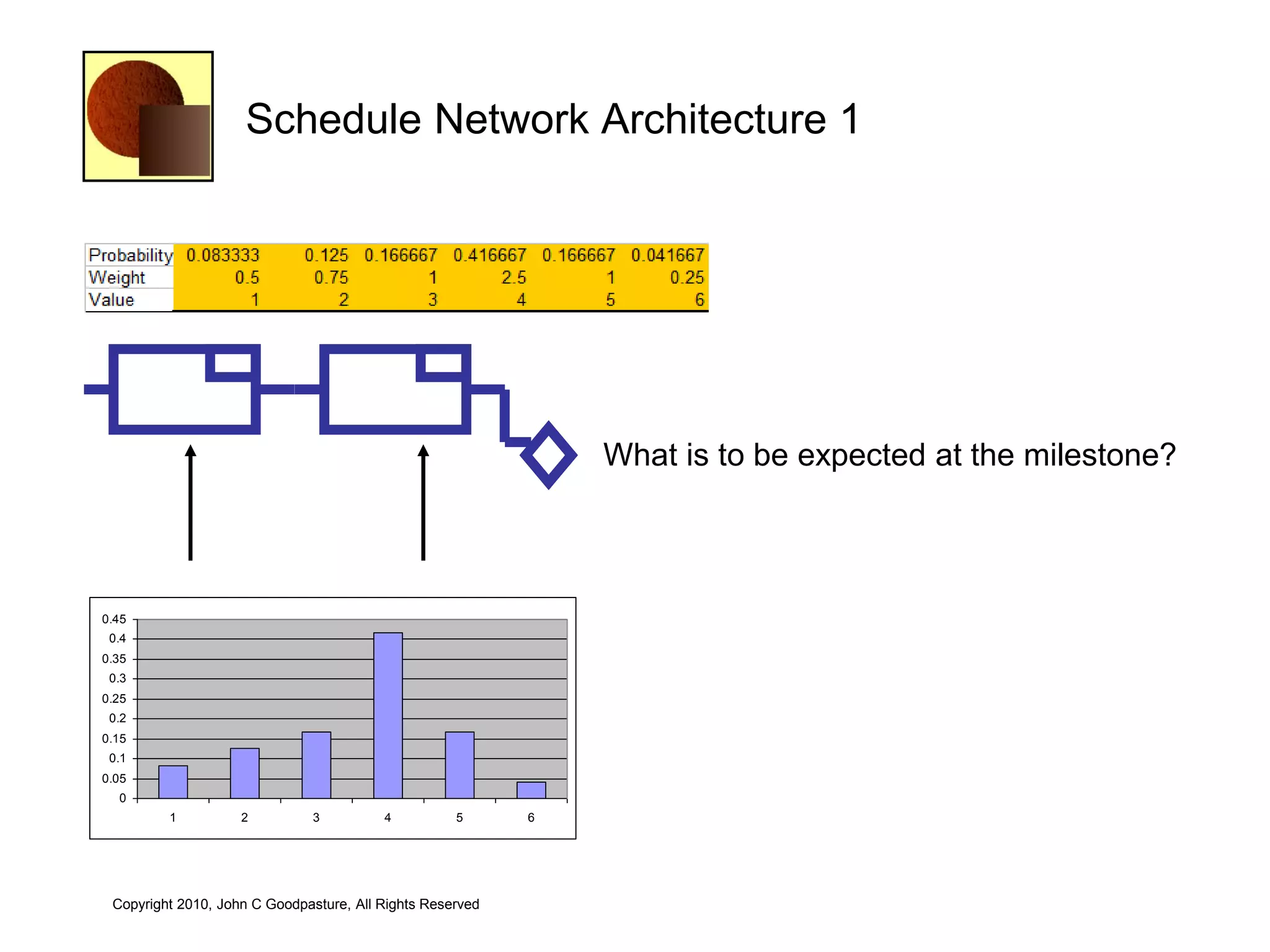
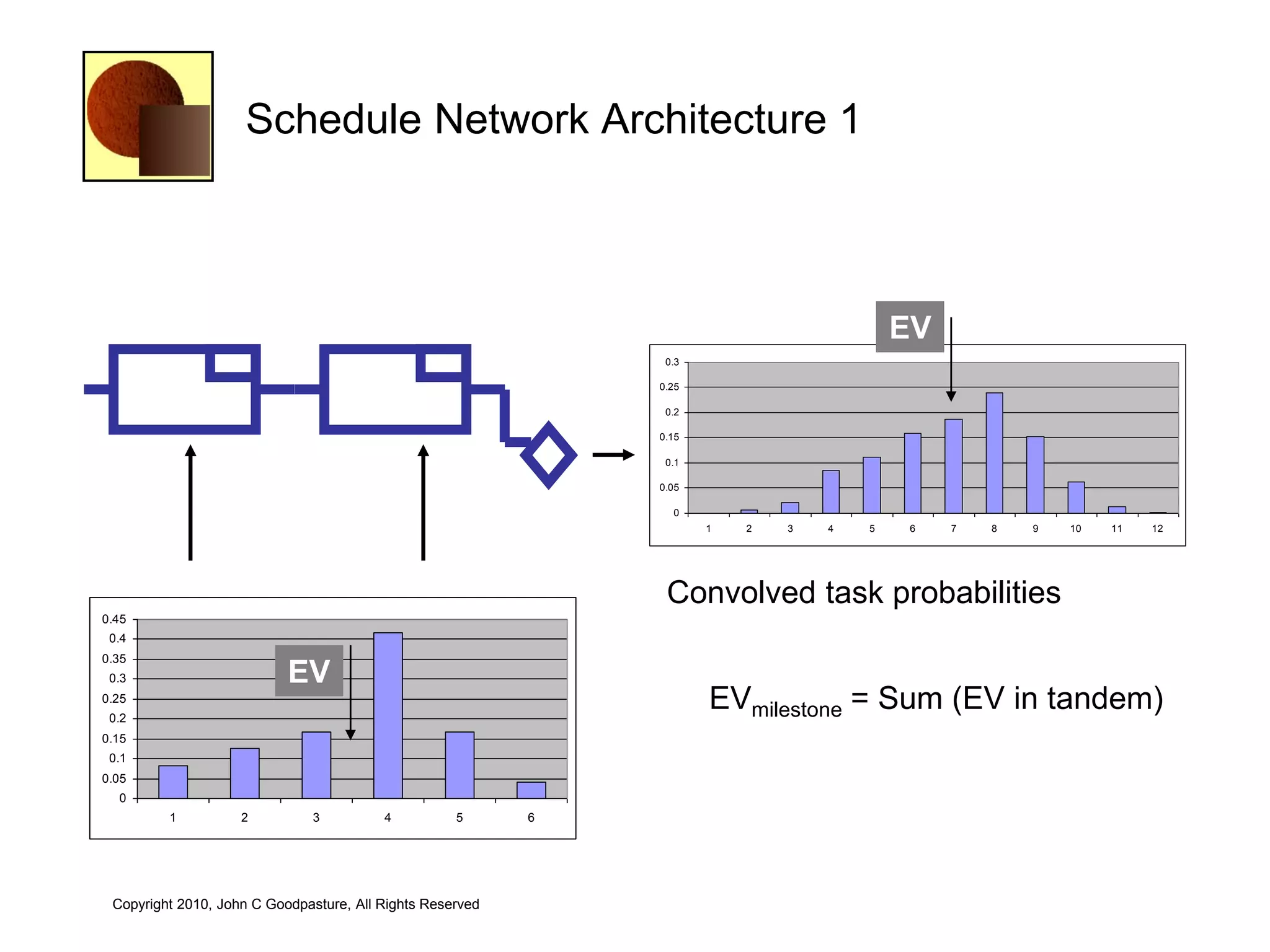
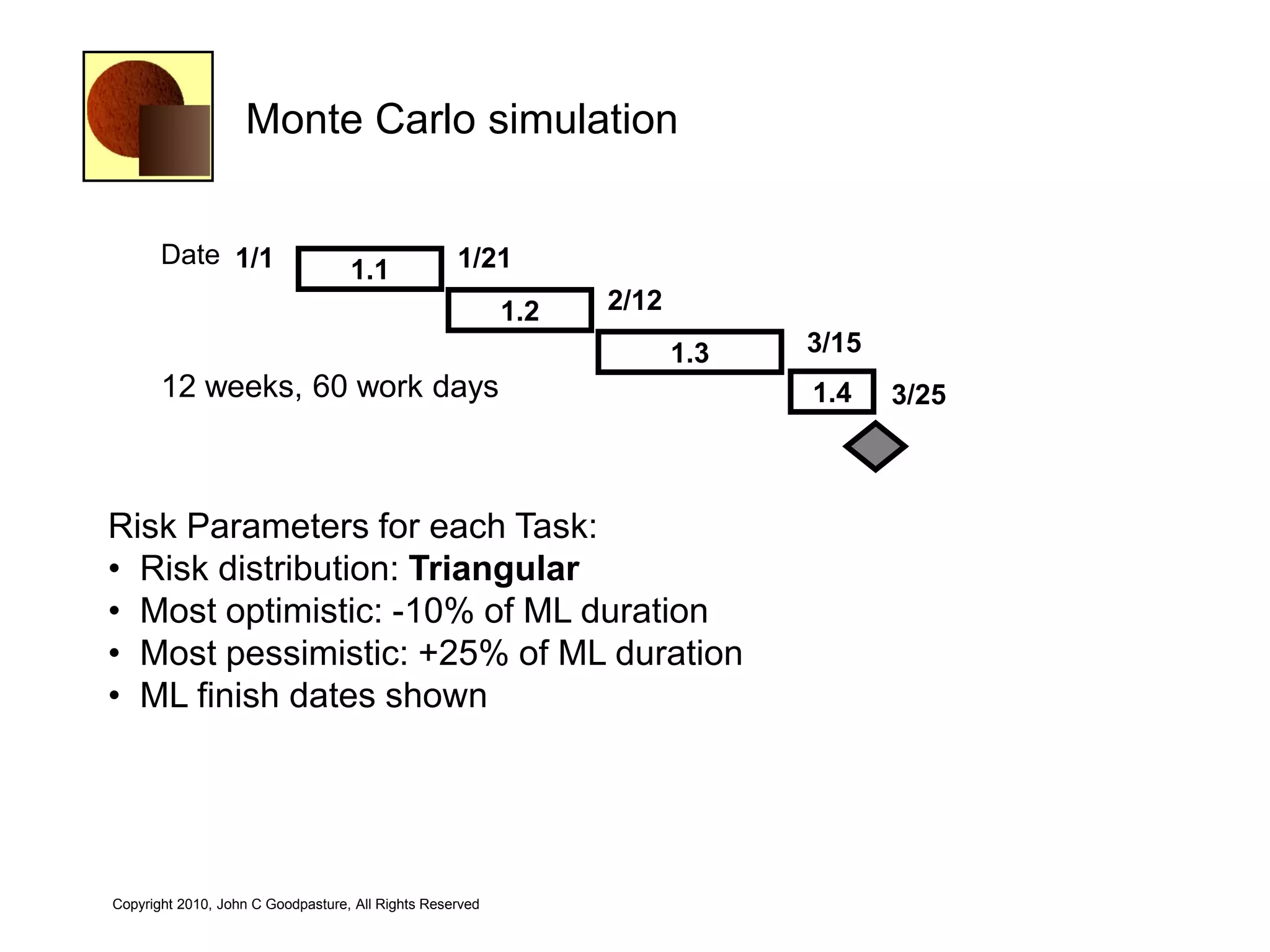
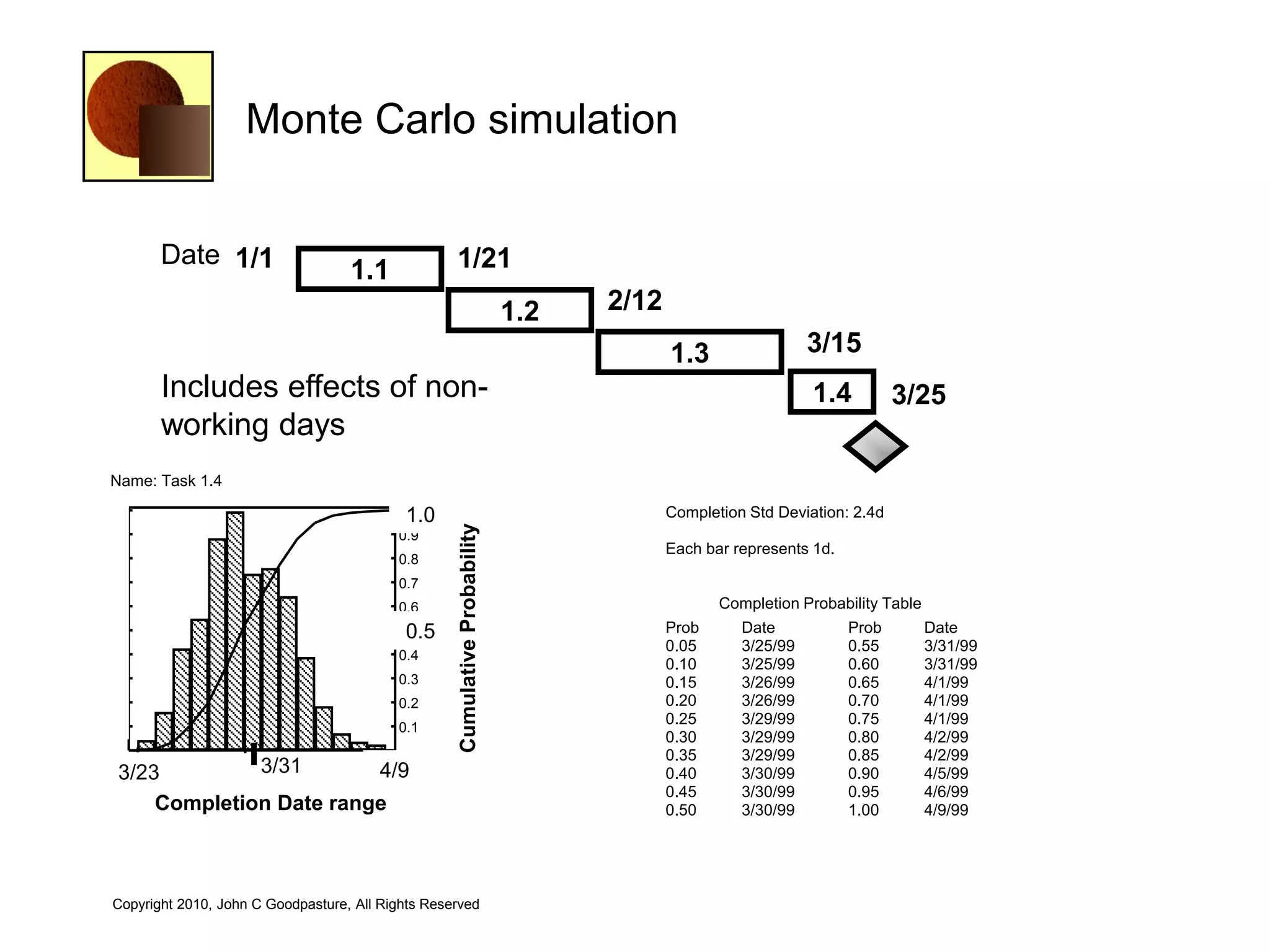
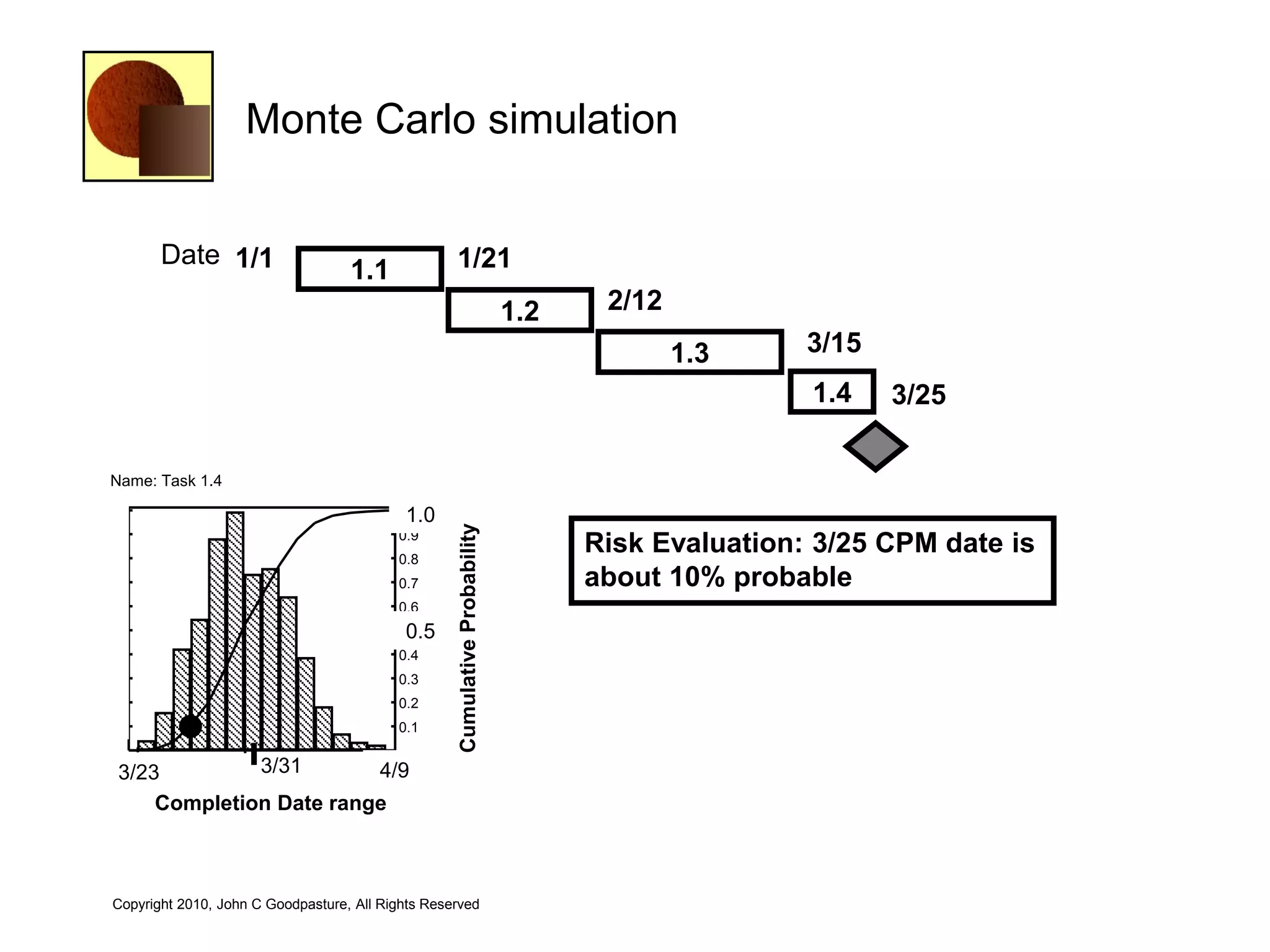
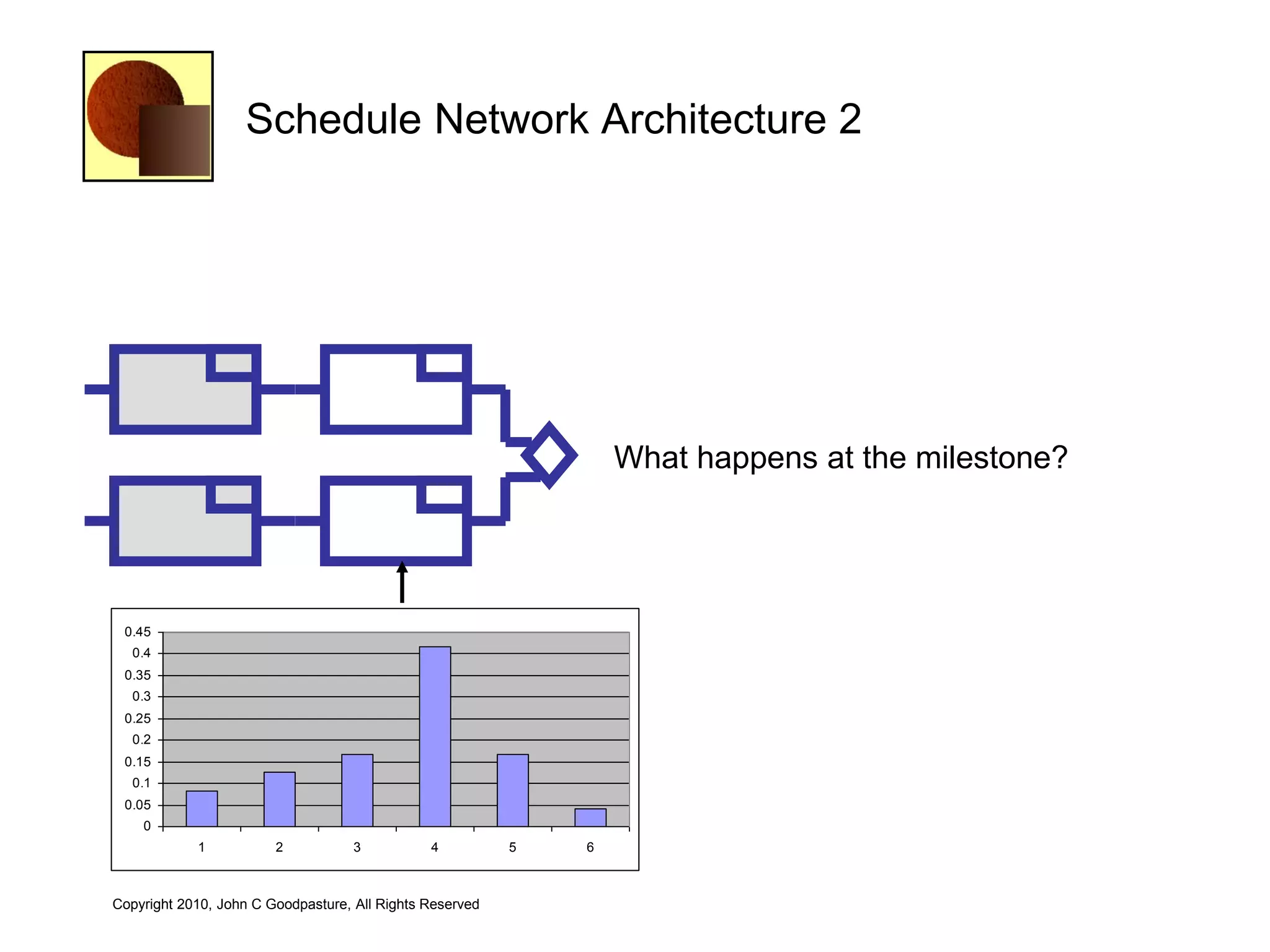
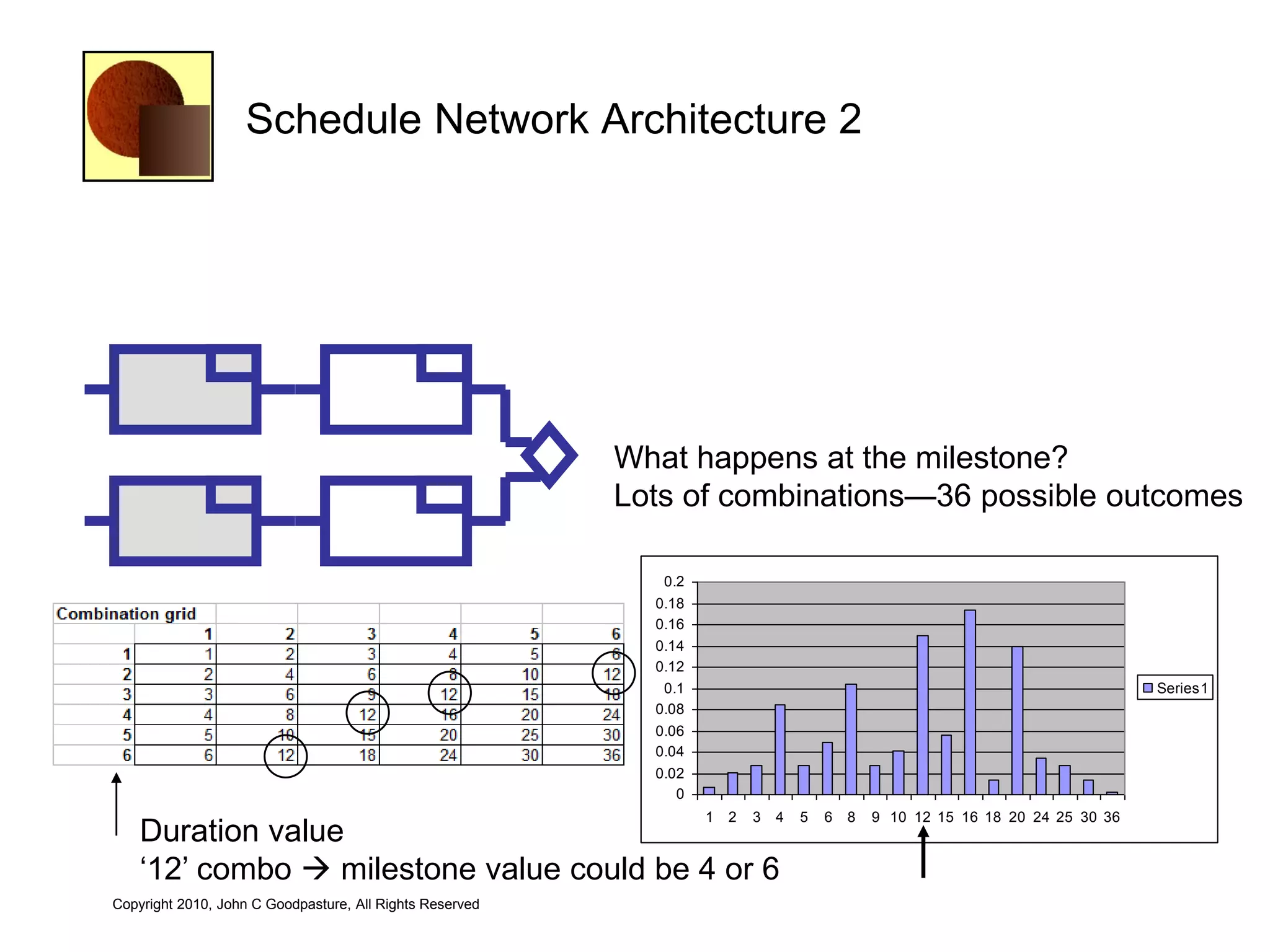
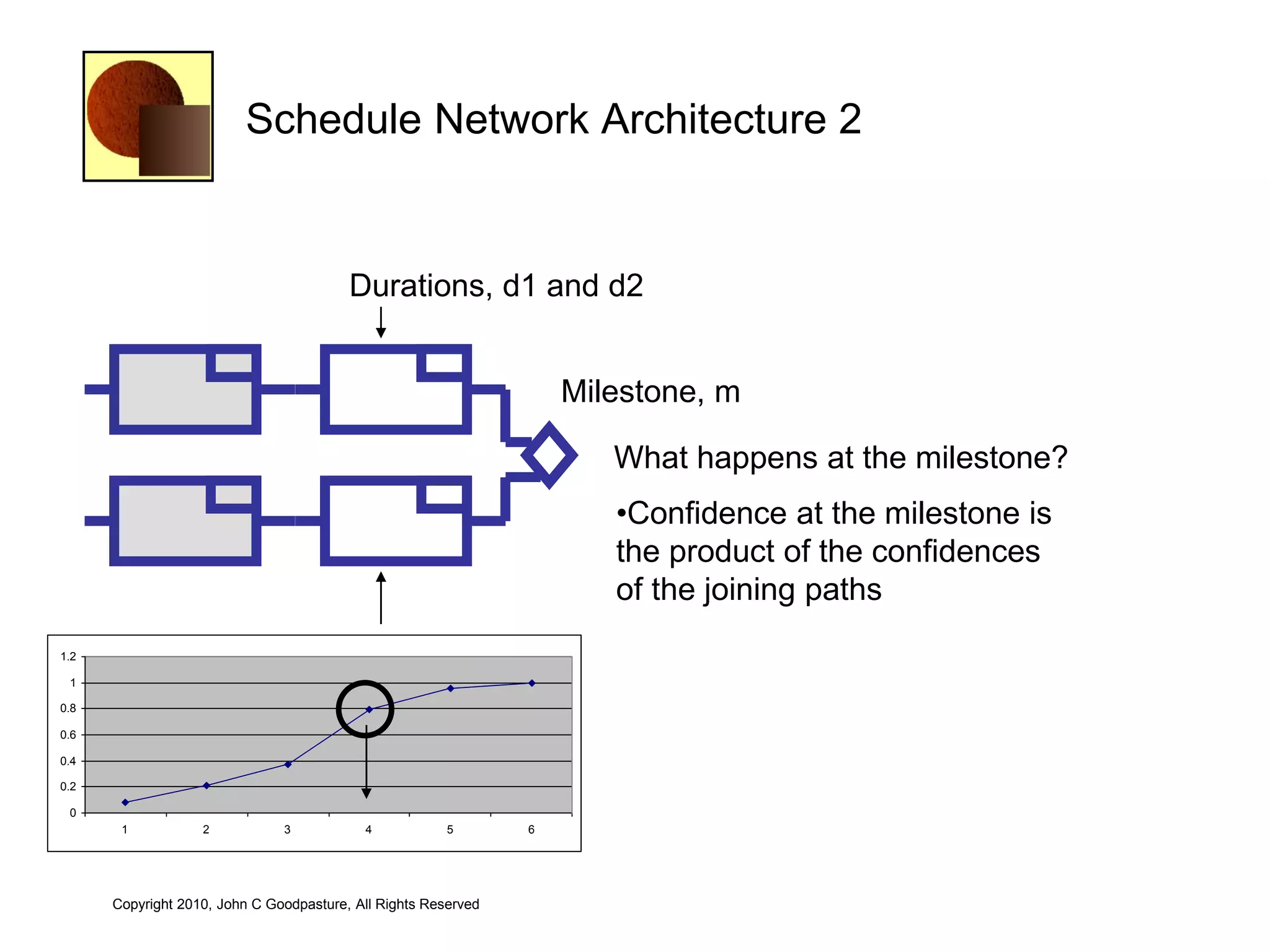
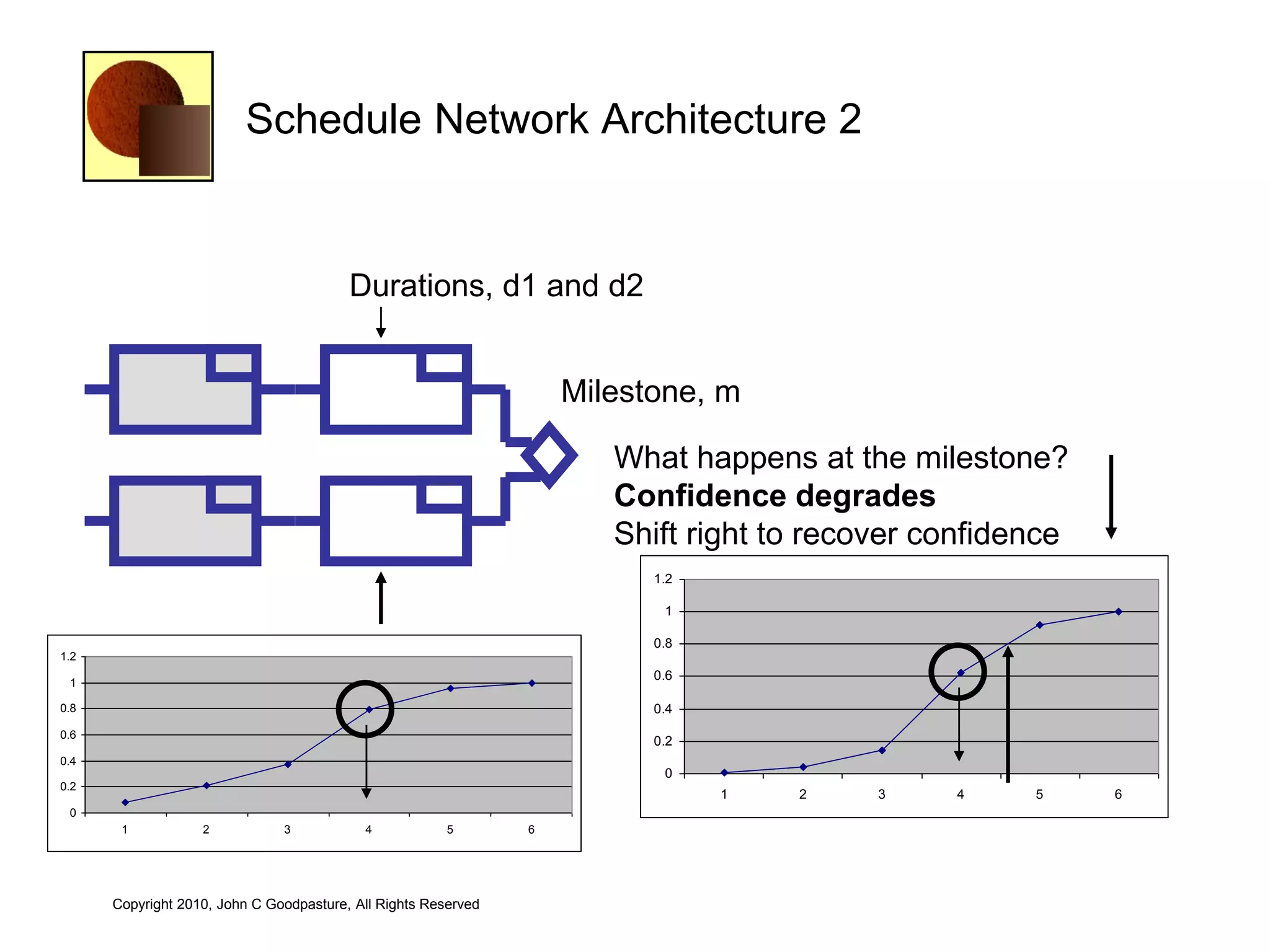
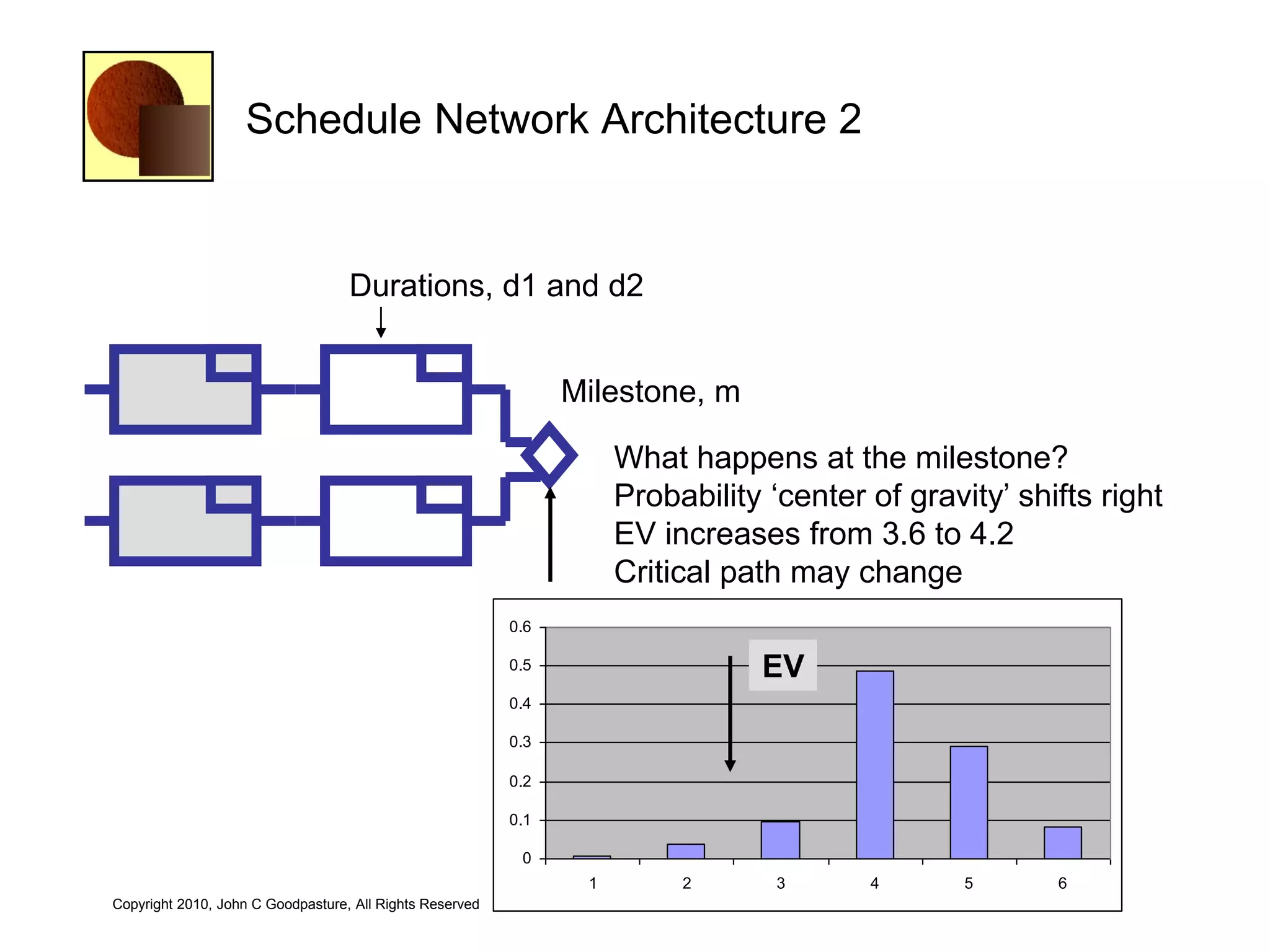
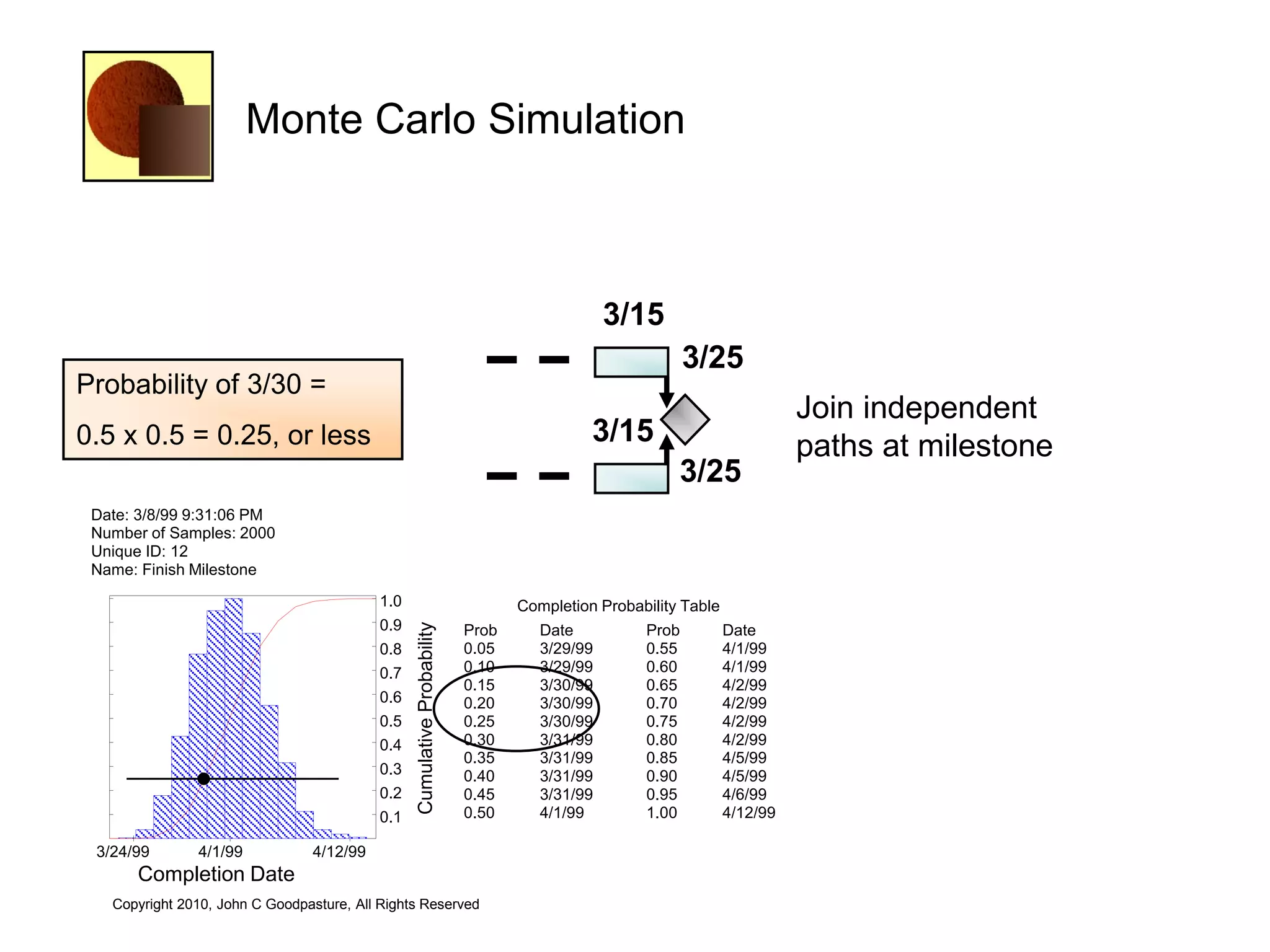
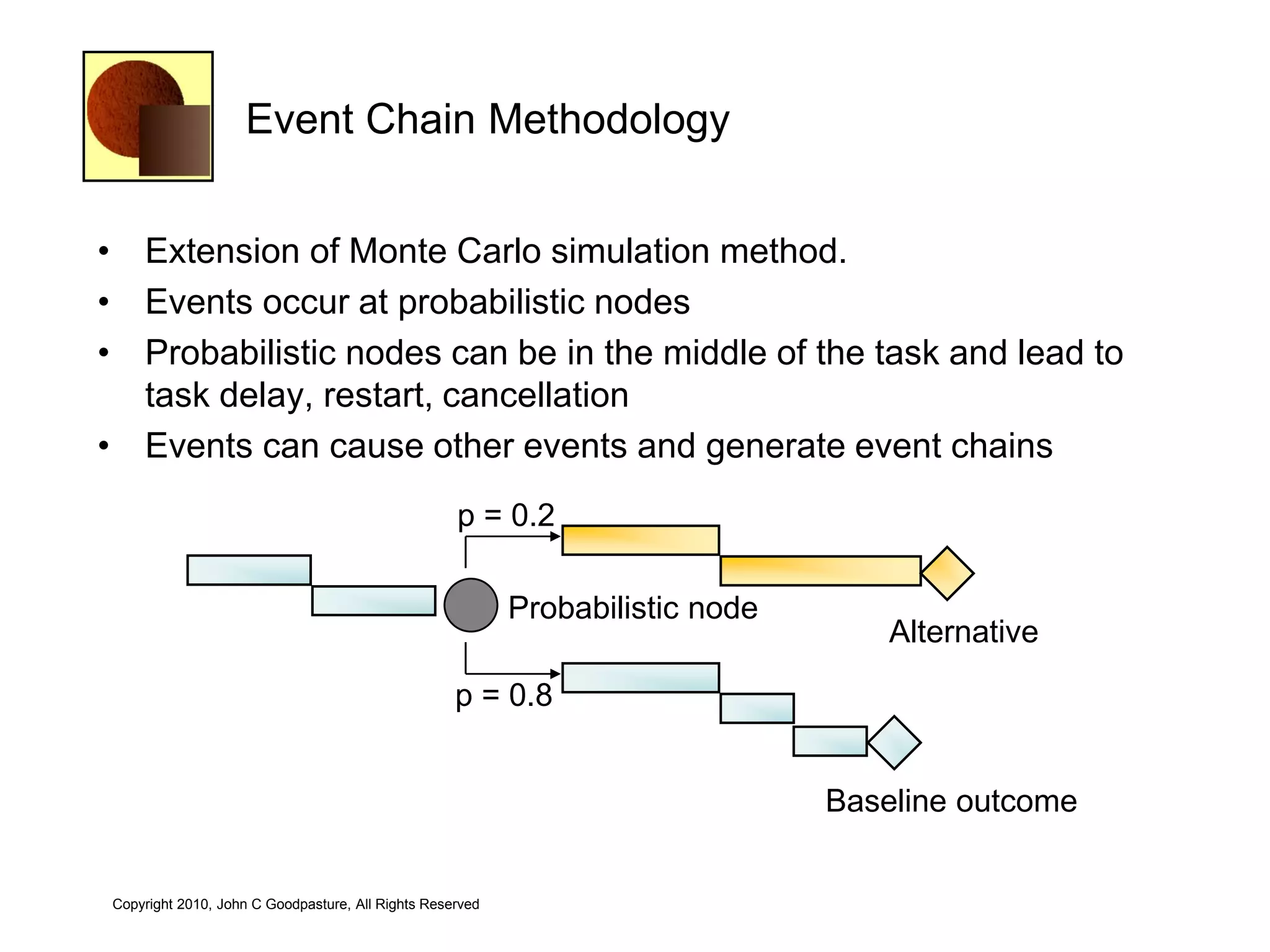
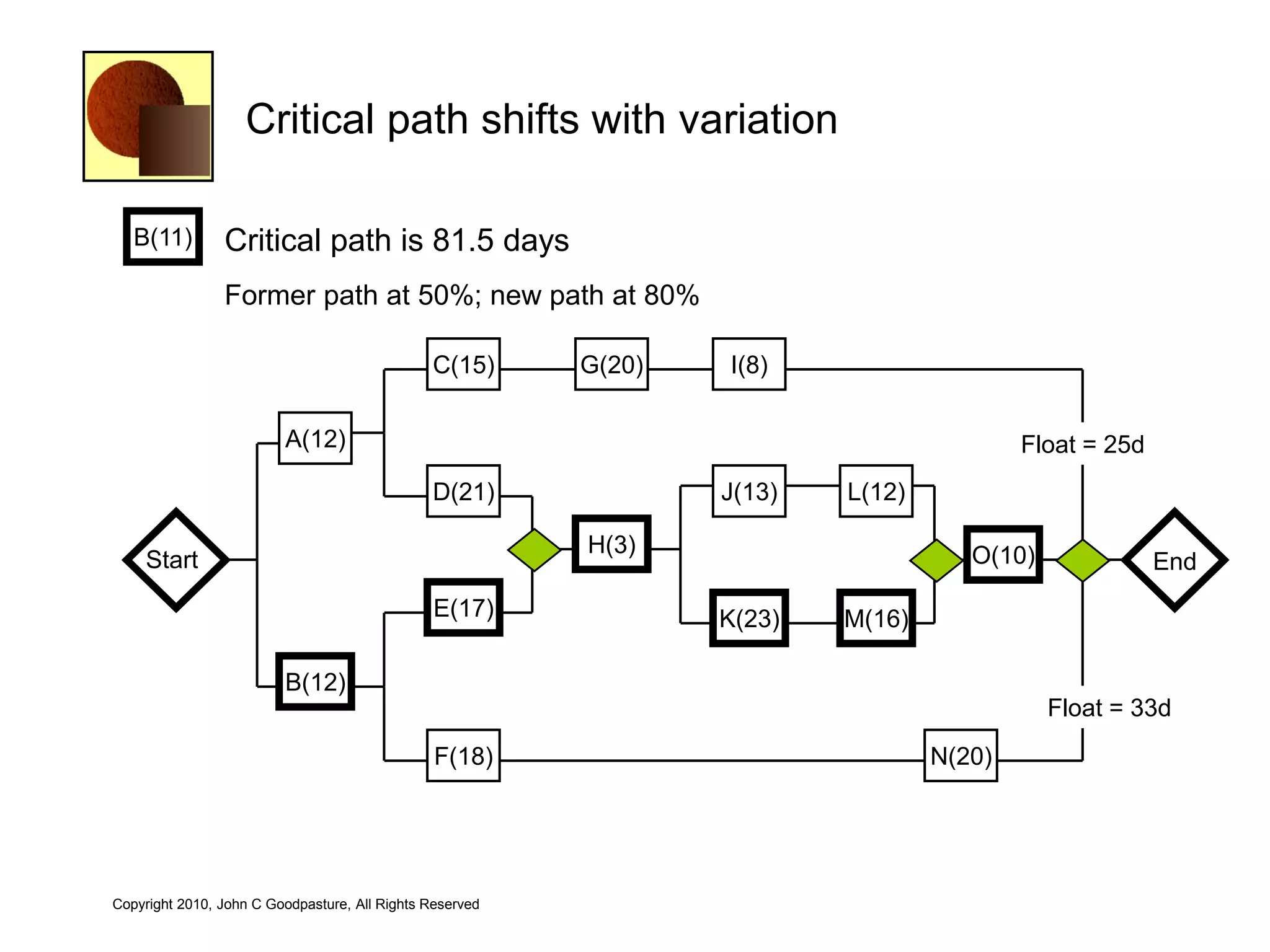
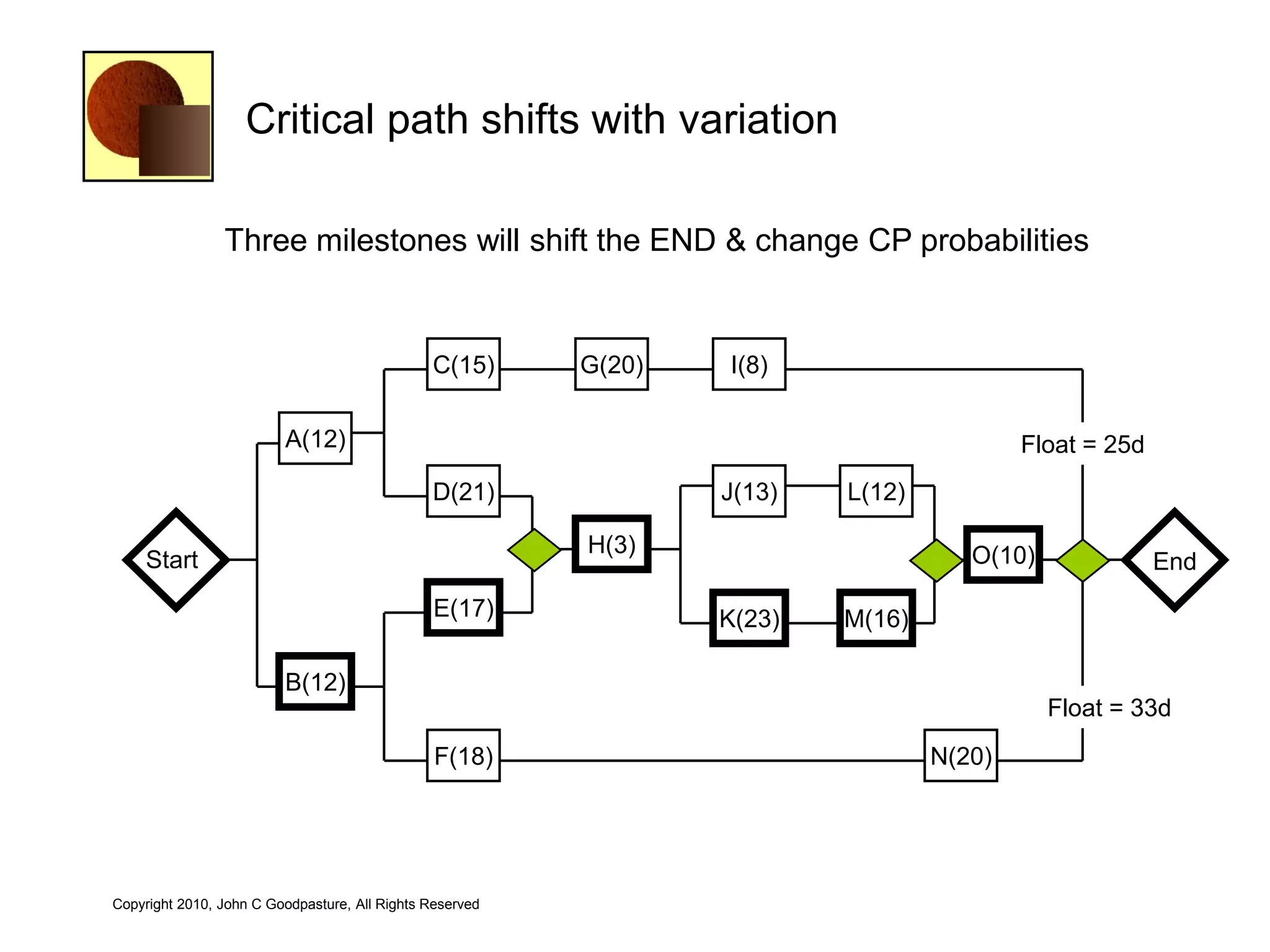
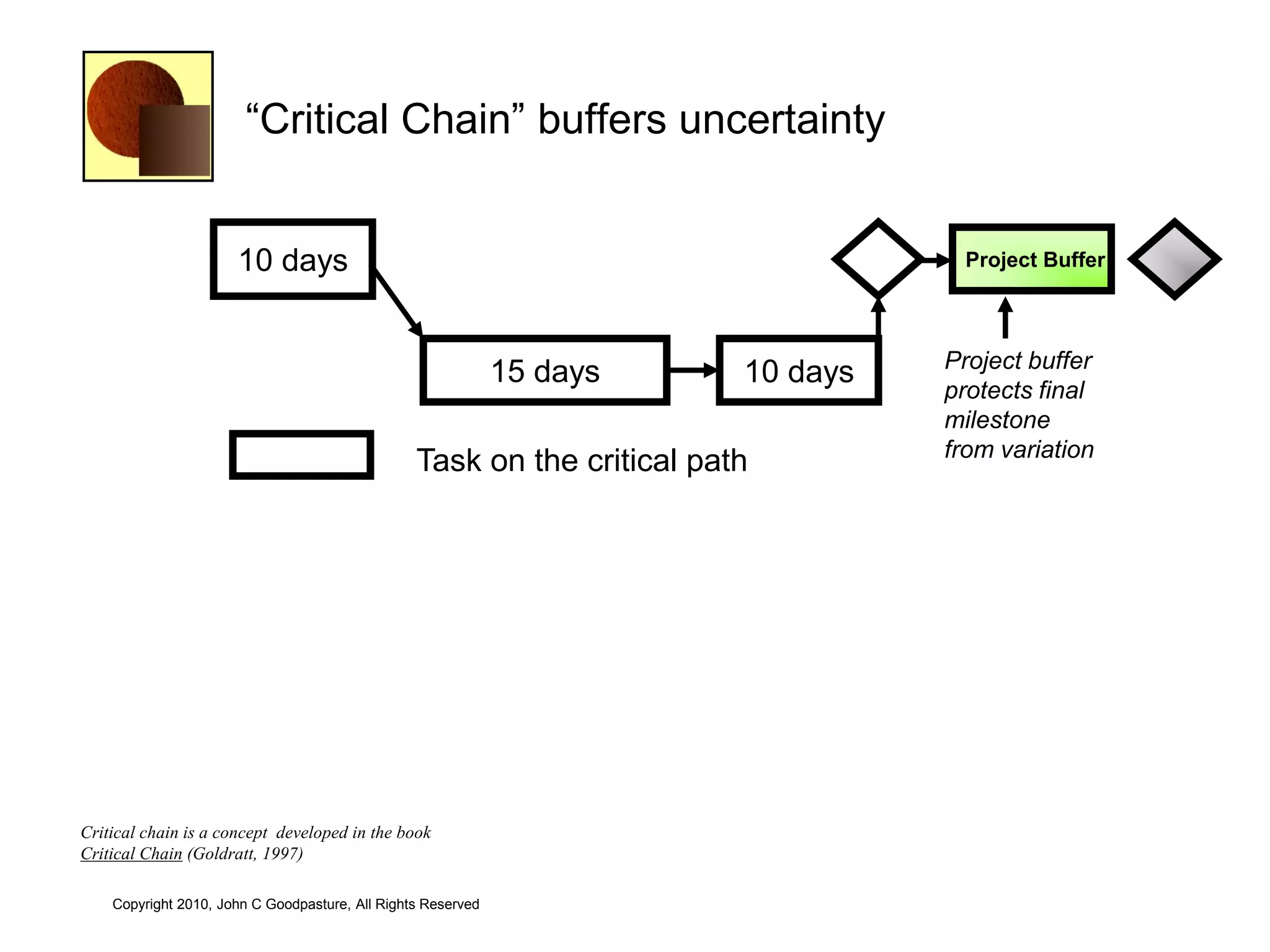
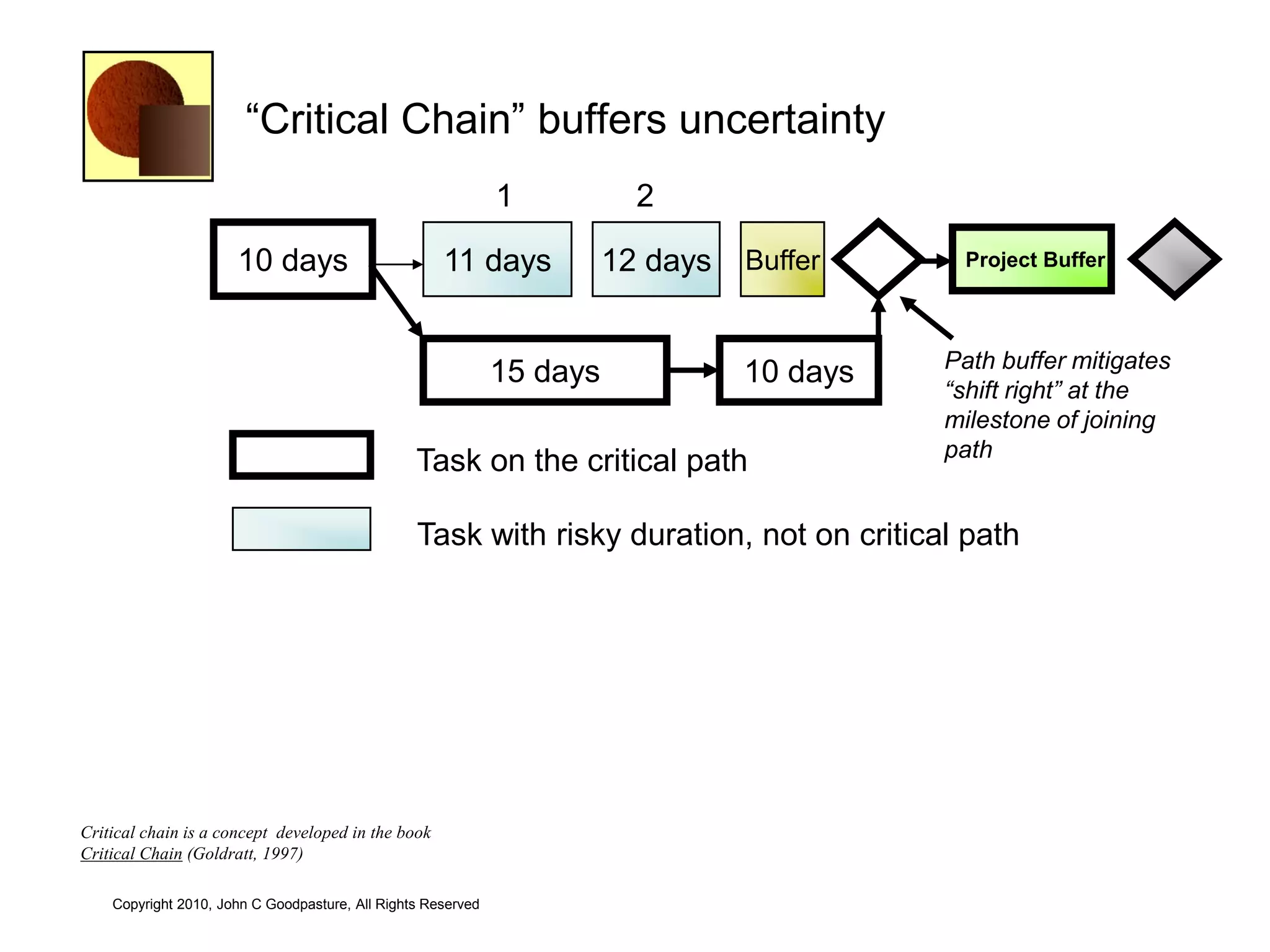
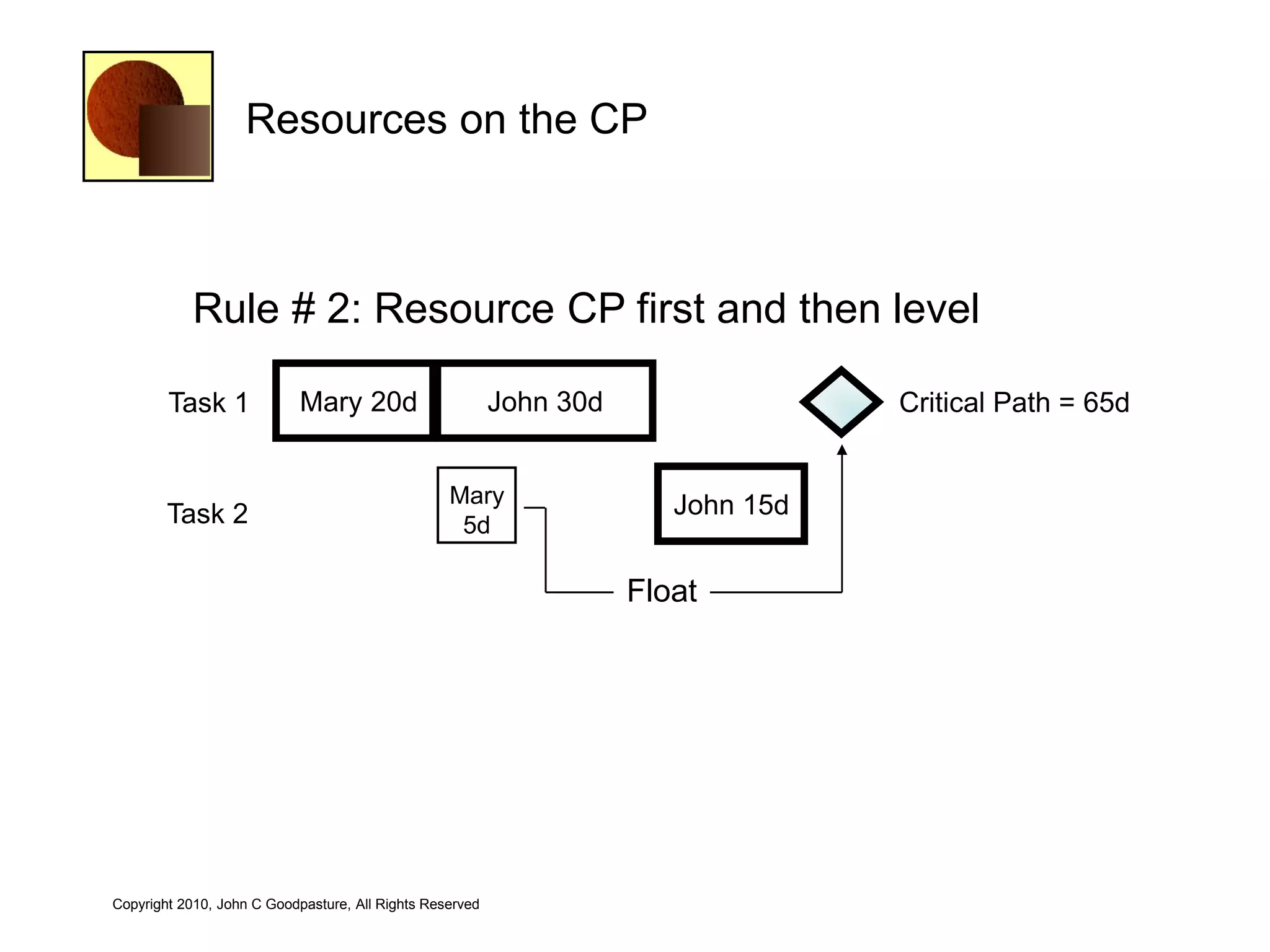
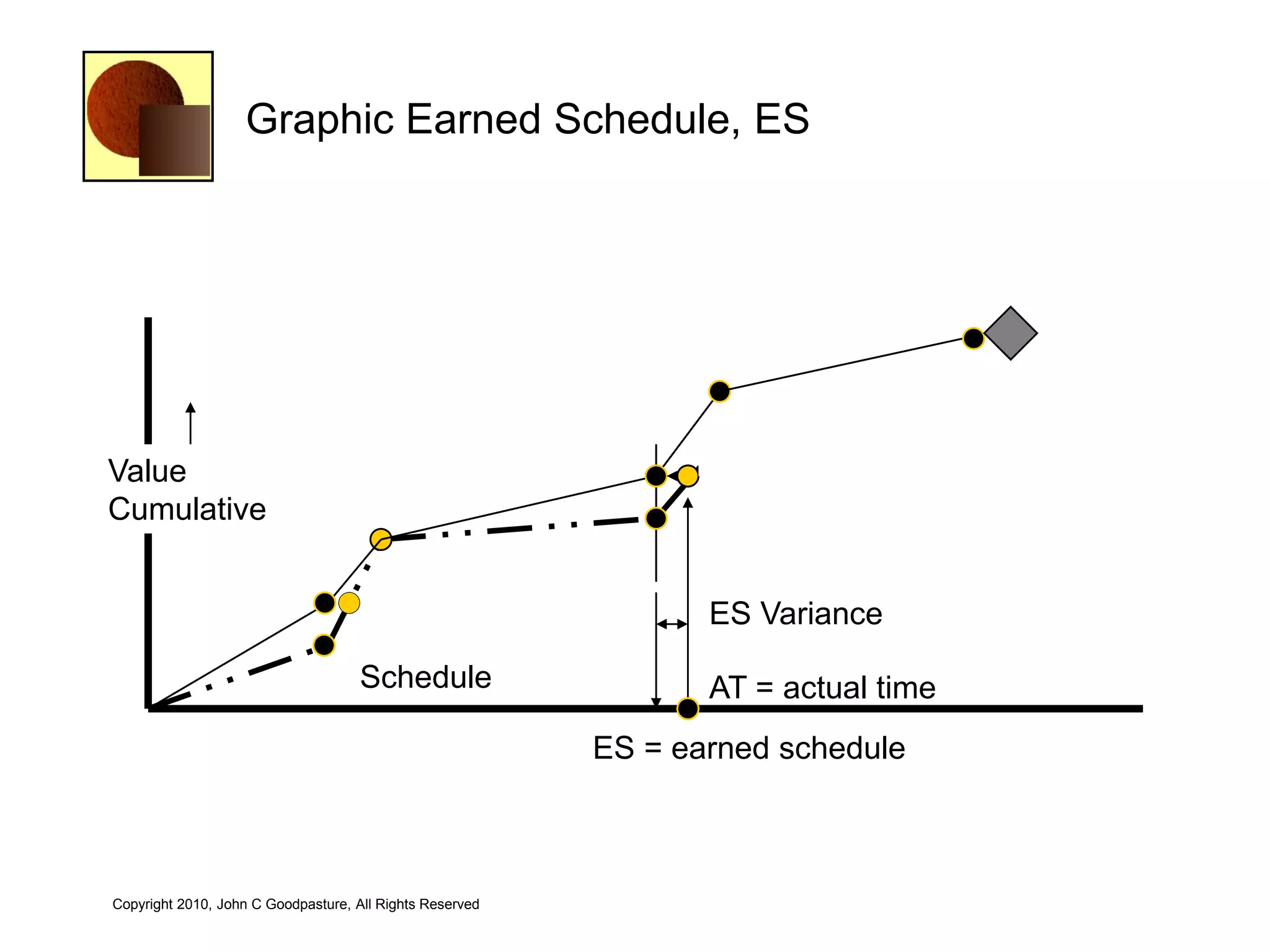
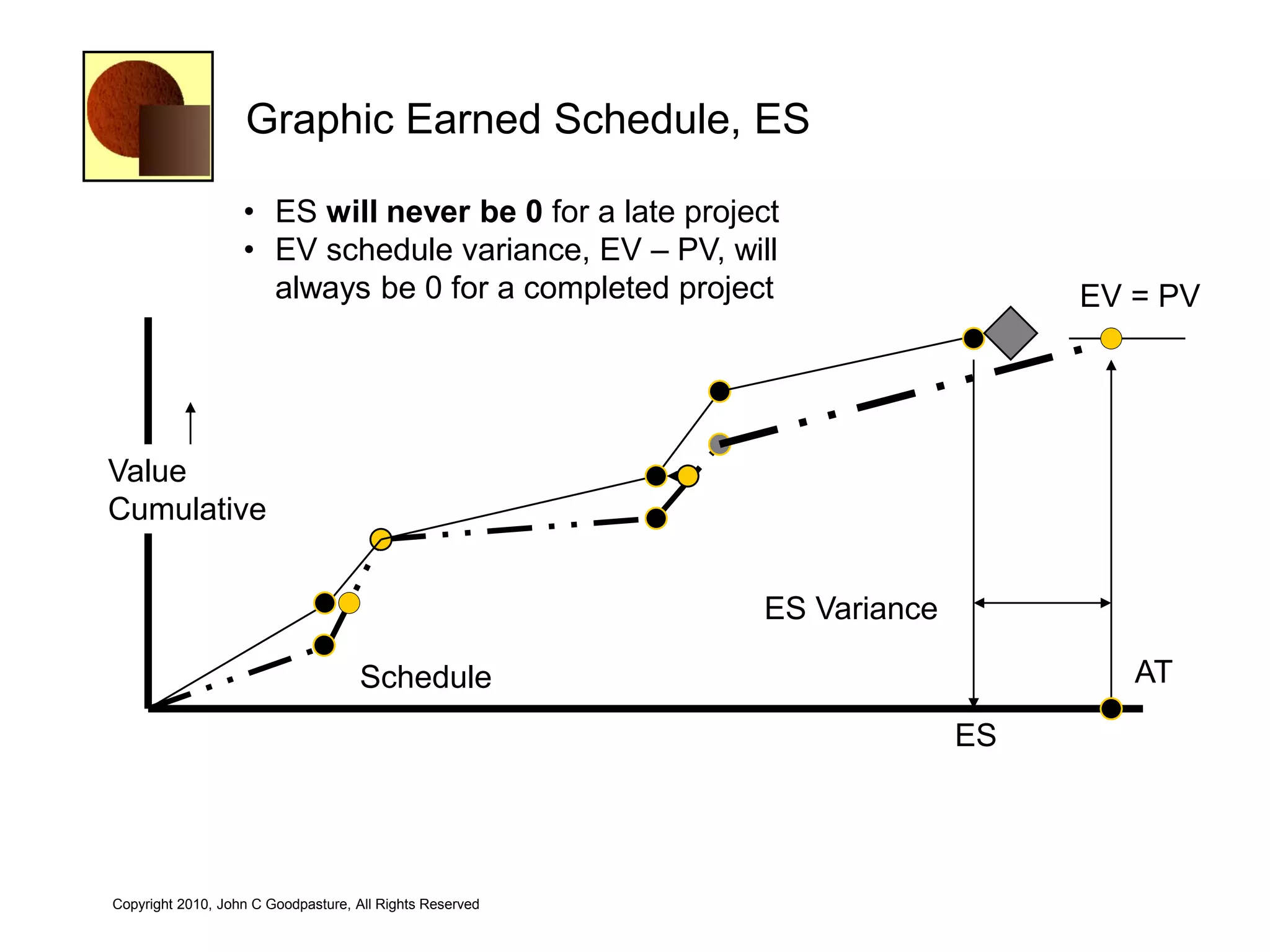
This document discusses quantitative risk analysis methods for project schedules. It introduces concepts like confidence intervals and S-curves that show the probability of completing a task within a certain date range. Monte Carlo simulation is presented as a method to model schedule risk by assigning probability distributions to task durations. The results provide expected values and confidence levels for completion dates. Network architectures with probabilistic nodes that can generate event chains are also proposed to extend Monte Carlo analysis.

1. Mitigating Risk in Schedules
Quantitative Methods in Project Management
Produced by
Square Peg Consulting, LLC
John C. Goodpasture
Managing Principal
www.sqpegconsulting.com
Copyright 2010, John C Goodpasture, All Rights Reserved
1

2. About Confidence
• Likelihood an event will occur within a range
• A number from 0 to 1
• Cumulative summation of probabilities within the range
Copyright 2010, John C Goodpasture, All Rights Reserved

3. Confidence ―S‖ Curve
1
Cumulative
Probability
0.75
0.5
0.25
0
-3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5
Normalized value
Value / Standard deviation, σ
Normalized cumulative probability from ‗bell‘ curve
Copyright 2010, John C Goodpasture, All Rights Reserved

4. Confidence ―S‖ Curve
1. 68% confidence: value between -1 to +1
2. 16% confidence: value > 1
3. 84% confidence: value < 1
2
1
Cumulative
Probability
0.75
0.5 1
0.25
0
-3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5
3 1 2
Copyright 2010, John C Goodpasture, All Rights Reserved

5. Generating Confidence
Probability Distribution
f(v)
Area = Height (probability) X
Probability
p f(v)
width (Δ Value)
Δ value
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Normalized random variable value
Calculate each ―Area increment‖
Δ value x p
Copyright 2010, John C Goodpasture, All Rights Reserved

6. Sum & Plot area increments
F(v) = 1 is the limiting value
f(v)Δv
F(v)
Area increments summed
Value
F(v) is the area under the f(v) curve
Copyright 2010, John C Goodpasture, All Rights Reserved

7. Schedule Network Architecture 1
What is to be expected at the milestone?
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

8. Schedule Network Architecture 1
EV
0.3
0.25
0.2
0.15
0.1
0.05
0
1 2 3 4 5 6 7 8 9 10 11 12
Convolved task probabilities
0.45
0.4
0.35
0.3 EV
0.25
0.2
EVmilestone = Sum (EV in tandem)
0.15
0.1
0.05
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

9. Schedule Network Architecture 1
0.3
0.25
0.2
0.15
0.1
0.05
0
1.2 1 2 3 4 5 6 7 8 9 10 11 12
1
0.8
0.6
1.2
0.4
1
0.2
0.8
0
0.6
1 2 3 4 5 6
0.4
0.2
0
Value = 1 2 3 4 5 6 7 8 9 10 11 12
Sum values at a constant confidence
Copyright 2010, John C Goodpasture, All Rights Reserved

10. Monte Carlo simulation
Date 1/1 1/21
1.1
1.2 2/12
1.3 3/15
12 weeks, 60 work days 1.4 3/25
Risk Parameters for each Task:
• Risk distribution: Triangular
• Most optimistic: -10% of ML duration
• Most pessimistic: +25% of ML duration
• ML finish dates shown
Copyright 2010, John C Goodpasture, All Rights Reserved

11. Monte Carlo simulation
Date 1/1 1/21
1.1
1.2 2/12
1.3 3/15
Includes effects of non- 1.4 3/25
working days 10:30:27 PM
Date: 3/9/99
Name: Task 1.4
170 1.0
1.0 Completion Std Deviation: 2.4d
Cumulative Probability
153 0.9
Each bar represents 1d.
136 0.8
119 0.7
102 0.6 Completion Probability Table
Sample Count
85 0.5
0.5 Prob Date Prob Date
0.05 3/25/99 0.55 3/31/99
68 0.4
0.10 3/25/99 0.60 3/31/99
51 0.3 0.15 3/26/99 0.65 4/1/99
34 0.2 0.20 3/26/99 0.70 4/1/99
0.25 3/29/99 0.75 4/1/99
17 0.1
0.30 3/29/99 0.80 4/2/99
3/23/99 3/31/99 4/9/99 0.35 3/29/99 0.85 4/2/99
3/23 3/31 4/9 0.40 3/30/99 0.90 4/5/99
0.45 3/30/99 0.95 4/6/99
Completion Date range 0.50 3/30/99 1.00 4/9/99
Copyright 2010, John C Goodpasture, All Rights Reserved

12. Monte Carlo simulation
Date 1/1 1/21
1.1
1.2 2/12
1.3 3/15
1.4 3/25
Date: 3/9/99 10:30:27 PM
Name: Task 1.4
170 1.0
1.0
Cumulative Probability
153 0.9
136 0.8
Risk Evaluation: 3/25 CPM date is
119 0.7 about 10% probable
102 0.6
Sample Count
85 0.5
0.5
68 0.4
51 0.3
34 0.2
17 0.1
3/23/99 3/31/99
3/31 4/9/99
3/23 4/9
Completion Date range
Copyright 2010, John C Goodpasture, All Rights Reserved

13. Budgets?
• Are the effects on budget totals any different when adding up a
string of $budgets from the WBS work packages?
Copyright 2010, John C Goodpasture, All Rights Reserved

14. Schedule Network Architecture 2
What happens at the milestone?
0.45
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

15. Schedule Network Architecture 2
What happens at the milestone?
Lots of combinations—36 possible outcomes
0.2
0.18
0.16
0.14
0.12
0.1 Series1
0.08
0.06
0.04
0.02
0
1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 30 36
Duration value
‗12‘ combo  milestone value could be 4 or 6
Copyright 2010, John C Goodpasture, All Rights Reserved

16. Schedule Network Architecture 2
Durations, d1 and d2
Milestone, m
What happens at the milestone?
•Confidence at the milestone is
the product of the confidences
of the joining paths
1.2
1
0.8
0.6
0.4
0.2
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

17. Schedule Network Architecture 2
Durations, d1 and d2
Milestone, m
What happens at the milestone?
Confidence degrades
Shift right to recover confidence
1.2
1
0.8
1.2
0.6
1
0.8 0.4
0.6
0.2
0.4
0
0.2
1 2 3 4 5 6
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

18. Schedule Network Architecture 2
Durations, d1 and d2
Milestone, m
What happens at the milestone?
Probability ‗center of gravity‘ shifts right
EV increases from 3.6 to 4.2
Critical path may change
0.6
0.5 EV
0.4
0.3
0.2
0.1
0
1 2 3 4 5 6
Copyright 2010, John C Goodpasture, All Rights Reserved

19. Monte Carlo Simulation
1/21 3/15
1/1 2/12 3/25
3/15
1/21
2/12
Date: 3/9/99 10:30:27 PM 3/25
Name: Task 1.4
170 1.0
1.0
• Milestone distribution for each
Cumulative Probability
153 0.9
136 0.8
119
102
0.7
0.6
independent path
Sample Count
85 0.5
0.5 • 50% confidence of 3/30 completion
68 0.4
51 0.3
34 0.2
17 0.1
3/23/99 3/31/99
3/31 4/9/99
3/23 4/9
Completion Date range
Copyright 2010, John C Goodpasture, All Rights Reserved

20. Monte Carlo Simulation
3/15
3/25
Probability of 3/30 =
Join independent
0.5 x 0.5 = 0.25, or less 3/15 paths at milestone
3/25
Date: 3/8/99 9:31:06 PM
Number of Samples: 2000
Unique ID: 12
Name: Finish Milestone
1.0 Completion Probability Table
0.9
Cumulative Probability
Prob Date Prob Date
0.8 0.05 3/29/99 0.55 4/1/99
0.7 0.10 3/29/99 0.60 4/1/99
0.15 3/30/99 0.65 4/2/99
0.6 0.20 3/30/99 0.70 4/2/99
0.5 0.25 3/30/99 0.75 4/2/99
0.4 0.30 3/31/99 0.80 4/2/99
0.35 3/31/99 0.85 4/5/99
0.3 0.40 3/31/99 0.90 4/5/99
0.2 0.45 3/31/99 0.95 4/6/99
0.1 0.50 4/1/99 1.00 4/12/99
3/24/99 4/1/99 4/12/99
Completion Date
Copyright 2010, John C Goodpasture, All Rights Reserved

21. Event Chain Methodology
• Extension of Monte Carlo simulation method.
• Events occur at probabilistic nodes
• Probabilistic nodes can be in the middle of the task and lead to
task delay, restart, cancellation
• Events can cause other events and generate event chains
p = 0.2
Probabilistic node
Alternative
p = 0.8
Baseline outcome
Copyright 2010, John C Goodpasture, All Rights Reserved

22. Build a path
80 days for the path shown
Task Duration is shown in days (#):
C(15) G(20) I(8)
A(12) Float = 25d
D(21) J(13) L(12)
H(3) O(9)
Start End
E(15) K(21) M(14)
B(11)
Float = 33d
F(18) N(20)
Copyright 2010, John C Goodpasture, All Rights Reserved

23. Build a network schedule
A(12) Every network at least one Critical Path
CP = 80 days; Additional paths are 49, 57, or 63, 73 days < 82 days
C(15) G(20) I(8)
A(12) Float = 25d
D(21) J(13) L(12)
H(3) O(9)
Start End
E(15) K(21) M(14)
B(11)
Float = 33d
F(18) N(20)
Copyright 2010, John C Goodpasture, All Rights Reserved

24. Critical path shifts with variation
B(11) Critical path is 81.5 days
Former path at 50%; new path at 80%
C(15) G(20) I(8)
A(12) Float = 25d
D(21) J(13) L(12)
H(3) O(10)
Start End
E(17) K(23) M(16)
B(12)
Float = 33d
F(18) N(20)
Copyright 2010, John C Goodpasture, All Rights Reserved

25. Critical path shifts with variation
Three milestones will shift the END & change CP probabilities
C(15) G(20) I(8)
A(12) Float = 25d
D(21) J(13) L(12)
H(3) O(10)
Start End
E(17) K(23) M(16)
B(12)
Float = 33d
F(18) N(20)
Copyright 2010, John C Goodpasture, All Rights Reserved

26. ―Critical Chain‖ buffers uncertainty
10 days Project Buffer
Project buffer
15 days 10 days
protects final
milestone
from variation
Task on the critical path
Critical chain is a concept developed in the book
Critical Chain (Goldratt, 1997)
Copyright 2010, John C Goodpasture, All Rights Reserved

27. ―Critical Chain‖ buffers uncertainty
1 2
10 days 11 days 12 days Buffer Project Buffer
Path buffer mitigates
15 days 10 days
“shift right” at the
milestone of joining
path
Task on the critical path
Task with risky duration, not on critical path
Critical chain is a concept developed in the book
Critical Chain (Goldratt, 1997)
Copyright 2010, John C Goodpasture, All Rights Reserved

28. Resources on the CP
Rule # 1: CP work begins at project beginning
Task 1 20d 30d Critical Path = 50d
Task 2 5d 15d
Copyright 2010, John C Goodpasture, All Rights Reserved

29. Resources on the CP
Rule # 2: Resource CP first and then level
Task 1 Mary 20d John 30d Critical Path = 65d
Mary John 15d
Task 2 5d
Float
Copyright 2010, John C Goodpasture, All Rights Reserved

30. CP responds to constraints
Rule # 3: Reorganize the network logic
Mary 20d John 30d Critical Path = 55d
Task 1
Mary
Task 2 John 15d
5d
Work does not begin first on the CP
Copyright 2010, John C Goodpasture, All Rights Reserved

31. Resource consequences
• Resource dependencies
lengthen the schedule
• In fact, any loss of
independence from any
cause will lengthen the
schedule!
• Resource constraints may
require work begin off the CP
Copyright 2010, John C Goodpasture, All Rights Reserved

32. Project manager’s mission:
To defeat an unfavorable forecast and deliver
customer value, taking reasonable risks to do so
Copyright 2010, John C Goodpasture, All Rights Reserved

33. Graphic Earned Schedule, ES
Value
Cumulative
ES Variance
Schedule AT = actual time
ES = earned schedule
Copyright 2010, John C Goodpasture, All Rights Reserved

34. Graphic Earned Schedule, ES
• ES will never be 0 for a late project
• EV schedule variance, EV – PV, will
always be 0 for a completed project EV = PV
Value
Cumulative
ES Variance
Schedule AT
ES
Copyright 2010, John C Goodpasture, All Rights Reserved

35. What‘s been learned?
• Confidence expresses probability over a range
• Confidence is based on the cumulative probability, a.k.a. the ‗area
under the curve‘
• Confidence is constant in tandem strings, whether budget or
schedule, but degrades rapidly at a parallel join
• Monte Carlo simulations give results very close to calculated
‗ideals‘
• Earned schedule will not have a 0 variance when all value is
earned
Copyright 2010, John C Goodpasture, All Rights Reserved