1. The document discusses scalar products (dot products) of vectors, work, power, and kinetic energy. It provides examples of calculating scalar products, work done by forces, and kinetic energy. 2. Key points made include that scalar product is also called dot product, work is force times distance, the unit of work and energy is the Joule, and kinetic energy is one-half mass times velocity squared. 3. Practice problems are provided to calculate scalar products, work, power, and kinetic energy given different vectors and scenarios.

1. Teacher: Elizer C. Himisola

2. What is your insight about the text?

3. Solve the following problem.
1. If a = 1 and b = 2, then what is a ∙ b?
2. If x =(2)(2k) and y = (3)(3k) then what
is x+y ?
3. If h = (3i+4j) and k = (2i+j) then what
is h+k?

4. DOT OR
SCALAR PRODUCT

5. Directions: Read the questions
carefully. Choose the letter of your
answer.
1.Dot product is also called as _____?
a.Scalar b. power
c. work d. energy

6. 2. It is done whenever energy is
transferred from one store to another.
a.Scalar b. power
c. work d. energy

7. 3. It is the energy that it
possesses due to its motion.
a. Scalar b. kinetic
c. work d. energy

8. 4. It is defined as the rate at
which work is done upon an
object.
a.Scalar b. kinetic
c. work d. power

9. 5. Given the two vector 𝑎 =
1
4
−3
and
𝑏 =
2
7
5
what is 𝑎 ∙ 𝑏 ?
a. 5 b. 10 c. 15 d. 20

10. 6. Calculate work: A 100 Newton
force is applied to move a 15 kg
object a distance of 5 meters?
a. 20 Joules b. 500 Joules
c. 75 Joules d. 1500 Joules

11. 7. A force exerted over a
distance to move an object is
a. power b. watt
c. work d. momentum

12. 8. A 5000N block is lifted 10m.
How much work was done?
a. 50000 J b. 5000 J
c. 500 J d. 50 J

13. 9. In which of these cases is work being
done?
a. A student sleeps
b. a student carries his chair into
another room
c. A student pushes a locked door that
does not move
d. A student sits on the carpet

14. 10. The unit used to measure
work is the
a. watt b. Newton
c. Joule d. meter

15. The dot product, also called scalar
product of two vectors is one of the
two ways we learn how to multiply
two vectors together, the other way
being the cross product, also called
vector product.

16. Notation
Given two vectors u u→ and v v→ we
refer to the scalar product by writing:
u ∙v = u→∙v→
In other words by writing a dot between
the two vectors, which explains why we
also call it the dot product.

17. Scalar Product: using the components of the
vectors. 2D Vectors
Given two vectors 𝑢 =
𝑢1
𝑢2
and 𝑣 =
𝑣1
𝑣2
their scalar product is: 𝑢 ∙ 𝑣 =
u1v1 + u2v2

18. Example:
Given two vectors
𝑎 =
2
−5
and 𝑏 =
1
−3
.
𝑎 ∙ 𝑏 = (2)(1) + (-5)(-3) = 2+15 = 17

19. Given two vectors 𝑢 =
𝑢1
𝑢2
𝑢3
and 𝑣 =
𝑣1
𝑣2
𝑣3
their scalar product is: 𝑢 ∙ 𝑣 = u1v1 + 𝑢2𝑣2 +
𝑢3𝑣3
3D Vectors

20. Example:
Given 𝑢 =
2
1
−3
and 𝑣 =
4
0
5
.
𝑢 ∙ 𝑣 = (2)(4)+(1)(0)+(-3)(5)
= 8+0-15
= -7

21. Scalar Product:
Using the magnitudes and angle.
𝑢 ∙ 𝑣 = 𝑢 ∙ 𝑣 x cos ,
where 𝜃 is the angle of 𝑢 𝑎𝑛𝑑 𝑣 .

22. Example:
Given two vectors a ∙ b such that
a = 4, b = 5
and the angle between them is θ
=60°.
a ∙ b = 4 x 5 x cos ( 60°) = 20 x 0. 5
= 10

23. Romans 3:20—Through the law we become
conscious of sin.
The Scalar product, like the
biblical law, makes us conscious of
the steps to obtain the correct
answer.

24. Work Done
by Force or Energy

25. For work to be done, a force must be
exerted and there must be motion or
displacement in the direction of the force.
The work done by a force acting on an
object is equal to the magnitude of the
force multiplied by the distance moved in
the direction of the force. Work has only
magnitude and no direction. Hence, work
is a scalar quantity.

26. W = F x d
The SI unit of work is Joule (J). For
example, if a force of 5 newtons is
applied to an object and moves 2
meters, the work done will be 10
newton-meter or 10 Joule.

27. Example:
An object is horizontally dragged
across the surface by a 100 N force
acting parallel to the surface. Find
out the amount of work done by the
force in moving the object through a
distance of 8 m.

28. Types of Energy
 Mechanical energy
 Mechanical wave energy
 Chemical energy
 Electric energy
 Magnetic energy
 Radiant energy
 Nuclear energy
 Ionization energy
 Elastic energy
 Gravitational energy
 Thermal energy
 Heat Energy

29. Energy is the ability to perform work. Energy
can neither be created nor destroyed, and it
can only be transformed from one form to
another. The unit of Energy is the same as of
Work, i.e. Joules. Energy is found in many
things, and thus there are different types of
energy.
The SI unit of energy is Joules (J), named in
honour of James Prescott Joule.

30. Kinetic energy
Kinetic energy (KE) of an object is
the energy that it possesses due to
its motion. It is defined as the work
needed to accelerate a body of a
given mass from rest to its stated
velocity.

31. KE = 0.5 • m • v2
where;
m = mass of object
v = speed of object

32. Example:
1.Determine the kinetic energy of a
625-kg roller coaster car that is
moving with a speed of 18.3 m/s.
KE = 0.5*m*v2
KE = (0.5) (625 kg) (18.3 m/s)2

33. 2.If the roller coaster car in
the above problem were
moving with twice the speed,
then what would be its new
kinetic energy?

34. If the speed is doubled, then the KE is
quadrupled. Thus, KE = 4 * (1.04653 x
105 J) = 4.19 x 105 Joules.
or
KE = 0.5*m*v2
KE = 0.5*625 kg*(36.6 m/s)2
KE = 4.19 x 105 Joules

35. 3. Missy Diwater, the former platform
diver for the Ringling Brother's Circus,
had a kinetic energy of 12 000 J just
prior to hitting the bucket of water. If
Missy's mass is 40 kg, then what is her
speed?

36. Power is a physical concept with
several different meanings, depending
on the context and the available
information. We can define power as
the rate of doing work, and it is the
amount of energy consumed per unit
of time.

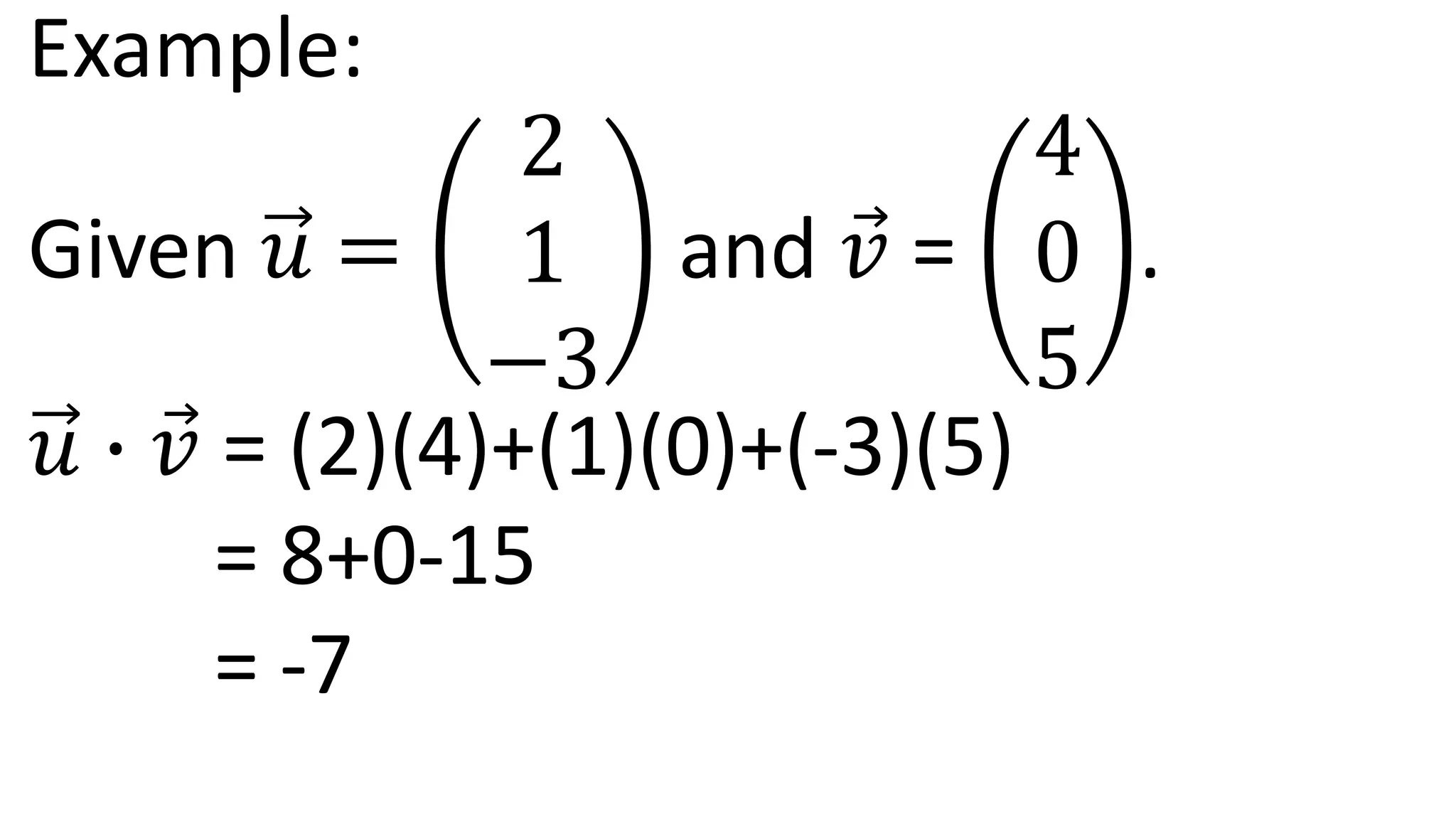
37. P = 𝑾/𝑻
Example
A garage hoist lifts a truck up 2
meters above the ground in 15
seconds. Find the power delivered
to the truck. [Given: 1000 kg as the
mass of the truck]

38. Example
A garage hoist lifts a truck up 2
meters above the ground in 15
seconds. Find the power delivered
to the truck. [Given: 1000 kg as
the mass of the truck]

39. First we need to calculate the work done,
which requires the force necessary to lift
the truck against gravity:
F = mg = 1000 x 9.81 = 9810 N.
W = Fd = 9810N x 2m = 19620 Nm =
19620 J.?//
The power is P = W/t = 19620J / 15s =
1308 J/s = 1308 W.

40. Example 1: If you lift a 10-
kilogram object to a height
of 5 meters in 2 seconds, the
power required would be?

41. Romans 3:20—Through the law we
become conscious of sin
The Scalar product, like
the biblical law, makes us
conscious of the steps to
obtain the correct answer.

42. Directions: Read the questions carefully. Choose the letter
of your answer.
1. The amount of work done depends on:
a. the size of the force on the object, the distance the
object moves
b. the size of the force on the object, the speed of
movement
c. the size of the object, the distance the object moves
d. the size of the force on the object, the friction acting
upon the object

43. 2. The gravitational force of any object
near Earth's surface is
a. unknown c. friction
b. c. 9.8 m/s2 d. Newton's first law

44. 3. Work done = Force x_______.
a. weight b. Distance
c. Newton d. friction

45. 4. Which of the following is the best
example of work being done.
a. doing homework
b. pushing a stationary box
c. holding a box
d. lifting a box

46. 5. The unit used to measure work is
the
a. Watt b. Newton
c. Joules d. meter

47. 6. Find the dot product
of <1, -2> and <3, 2>
a. 1 b. -1
c. 0 d. (1,-1)

48. 7. What is the answer when you
take dot product between two
vectors?
a. a vector b. a vector and scale
c. a scalar d. none

49. 8. Which of the following
symbols represent vectors?
a. 𝑣 b. v
c. vcts d. β

50. 9. Find the vector u × v when
u = [3,−1,1] and v = [2,5,1].
a. 1 b. 0
c. 3 d. 2

51. 10. Find the vector u × v when
u = [3,4,6] and v = [0,1,1]
a. 8 b. 9
c. 10 d. 11