More Related Content
PDF
PyMCがあれば,ベイズ推定でもう泣いたりなんかしない PDF
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) PDF
PDF
PDF
BlackBox モデルの説明性・解釈性技術の実装 PDF
PDF
What's hot
PDF
PDF
[DL輪読会]Wasserstein GAN/Towards Principled Methods for Training Generative Adv... PPTX
強化学習の基礎と深層強化学習(東京大学 松尾研究室 深層強化学習サマースクール講義資料) PDF
PDF
PDF
PDF
SSII2021 [TS2] 深層強化学習 〜 強化学習の基礎から応用まで 〜 PDF
PDF
PDF
PDF
PDF
PPTX
Swin Transformer (ICCV'21 Best Paper) を完璧に理解する資料 PDF
PPTX
【DL輪読会】SimCSE: Simple Contrastive Learning of Sentence Embeddings (EMNLP 2021) PPTX
PDF
最新リリース:Optuna V3の全て - 2022/12/10 Optuna Meetup #2 PPTX
Curriculum Learning (関東CV勉強会) PDF
PPTX
【DL輪読会】Flamingo: a Visual Language Model for Few-Shot Learning 画像×言語の大規模基盤モ... Viewers also liked
PDF
「深層学習」勉強会LT資料 "Chainer使ってみた" PPTX
PPTX
PDF
PDF
科学と機械学習のあいだ:変量の設計・変換・選択・交互作用・線形性 PPTX
PPTX
面倒くさいこと考えたくないあなたへ〜Tpotと機械学習〜 PDF
GBDTを使ったfeature transformationの適用例 PDF
Randomforestで高次元の変数重要度を見る #japanr LT PPTX
PPTX
PDF
PDF
PDF
PDF
実践多クラス分類 Kaggle Ottoから学んだこと ZIP
PDF
「はじめてでもわかる RandomForest 入門-集団学習による分類・予測 -」 -第7回データマイニング+WEB勉強会@東京 Similar to 不均衡データのクラス分類
PPTX
SMOTE resampling method slides 02-19-2018 PDF
A systematic study of the class imbalance problem in convolutional neural net... PDF
PPTX
PPTX
PDF
PPTX
Long-Tailed Classificationの最新動向について PDF
PDF
PDF
PDF
PDF
PDF
Introduction to ensemble methods for beginners PDF
PDF
Jubatusにおける大規模分散オンライン機械学習 PPTX
0610 TECH & BRIDGE MEETING PPTX
Feature Selection with R / in JP PPTX
DLLab 異常検知ナイト 資料 20180214 PDF
レコメンドアルゴリズムの基本と周辺知識と実装方法 PDF
More from Shintaro Fukushima
PDF
20230216_Python機械学習プログラミング.pdf PDF
PDF
Materials Informatics and Python PDF
PDF
最近のRのランダムフォレストパッケージ -ranger/Rborist- PDF
Why dont you_create_new_spark_jl PDF
PDF
PDF
PDF
PDF
PDF
data.tableパッケージで大規模データをサクッと処理する PDF
アクションマイニングを用いた最適なアクションの導出 PDF
PDF
PDF
PDF
統計解析言語Rにおける大規模データ管理のためのboost.interprocessの活用 PDF
PDF
PDF
不均衡データのクラス分類
- 1.
- 2.
アジェンダ
自己紹介
クラス分類
不均衡データ
不均衡データへの対処方法
- 3.
- 4.
- 5.
- 6.
- 7.
クラス分類を行うための手法は
数多く提案されている.
決定木
ナイーブベイズ
サポートベクタマシン
ブースティング
ランダムフォレスト etc.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
> library(kernlab)
> #データの読み込み(データは"../data/"ディレクトリに置いておく)
> abalone <- read.csv("../data/abalone.data", header=FALSE)
> # 19番目のクラスを正例に,それ以外のクラスを負例とする
> label <- abalone[, 9]
> label[label==19] <- "positive"
> label[label!="positive"] <- "negative"
> label <- factor(label)
> table(label)
label
negative positive
4145 32
正例32サンプル,
負例4145サンプルのデータ
- 14.
> set.seed(123)
> #クロスバリデーションの実行(多項式カーネルを用い,次数は2とする)
> idx <- sample(1:10, nrow(abalone), replace=TRUE)
> for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
+ abalone.test <- abalone[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train, kernel="polydot",
kpar=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+}
> # 予測結果の集計
> table(pred)
pred
negative 全てを負例と判別!!
4177
- 15.
- 16.
- 17.
①正例を誤答したときの
ペナルティを重くする
(cost-sensitive learning)
②正例と負例のサンプル数を
調整する
- 18.
①正例を誤答したときの
ペナルティを重くする
(cost-sensitive learning)
SVMでは,
ksvm関数(kernlabパッケージ)の
class.weights引数に指定
- 19.
> label.table <- table(label)
> # 正例の重み(負例と正例のサンプル数の比とする)
> weight.positive <- as.numeric(label.table[1]/label.table[2])
> # 10-fold クロスバリデーションの実行
> for (i in 1:10) { 正例と負例の
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
サンプル数に反比例した
+ abalone.test <- abalone[is.test, -9] ペナルティの重みを指定
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
+ class.weights=c("positive"=weight.positive,
+ "negative"=1),
+ kernel="polydot", kapr=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+ }
> table(label, pred) 何も工夫しないよりは
pred
label negative positive 良くなったが,まだまだ
negative 3118 1027 (モデルパラメータの
positive 19 13 チューニングの余地もまだまだあり)
- 20.
②正例と負例のサンプル数を
調整する
オーバーサンプリング
→正例を増やす
アンダーサンプリング
→負例を減らす
両方
- 21.
- 22.
- 23.
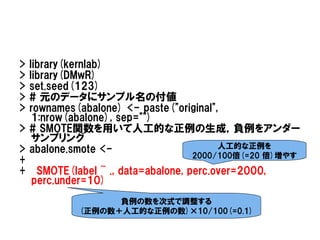
> library(kernlab)
> library(DMwR)
>set.seed(123)
> # 元のデータにサンプル名の付値
> rownames(abalone) <- paste("original",
1:nrow(abalone), sep="")
> # SMOTE関数を用いて人工的な正例の生成,負例をアンダー
サンプリング
> abalone.smote <- 人工的な正例を
2000/100倍(=20 倍)増やす
+
+ SMOTE(label ~ ., data=abalone, perc.over=2000,
perc.under=10)
負例の数を次式で調整する
(正例の数+人工的な正例の数)×10/100(=0.1)
- 24.
>idx <- sample(1:10,nrow(abalone.smote), replace=T)
>pred <- rep(NA, nrow(abalone.smote))
># 10-fold クロスバリデーションの実行
>for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone.smote[!is.test, ]
+ abalone.test <- abalone.smote[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
kernel="polydot", kpar=list(degree=2))
+ pred[is.test] <- predict(fit.ksvm, abalone.test)
+}
- 25.
> # SMOTEでの補間点も含むデータに対する分割表
>table(abalone.smote$label, pred)
negative positive
negative 19 13
positive 1 351
> # 元々のデータに対する分割表
> is.original <- rownames(abalone.smote) %in%
+ rownames(abalone)
> table(abalone.smote[is.original, "label"],
+ pred[is.original])
negative positive
negative 19 13 まだまだチューニングの
positive 0 32 余地はあるが,
それでも精度はかなり
向上
- 26.
- 27.
- 28.
- 29.
- 30.
Weighted RandomForest
正例,負例をそれぞれ誤って分類する際のペ
ナルティを以下の2箇所で考慮する.
Gini係数を評価基準として決定木の枝を作成する
とき
予測ラベルを決定する際に重み付き多数決を取
るとき
Balanced Random Forest
各ツリーを構築する際, 正例のデータ数と同じ
だけ負例のデータをサンプリングして学習する.
- 31.
- 32.
引数classwtを調整しても
あまり効果はない?
randomForestパッケージの管理者によると・・・
(http://bit.ly/xJ2mUJ)
現在のclasswtオプションはパッケージが開発された当初から存在しているが,
公式のfortranのコード(バージョン4以降)の実装とは異なる.
クラスの重みを考慮するのは,ノード分割時にGini係数を算出する際のみである.
我々は,クラスの重みをGini係数の算出においてのみ用いても,極端に不均衡
なデータ(例えば1:100やそれ以上)に対してはあまり役に立たないことが分かっ
た.そこで,Breiman教授はクラスの重みを考慮する新しい方法を考案した.こ
の方法は新しいfortranコードに実装されている.
現在のパッケージのclasswtにクラスの重みを指定しても,我々が望んでいた結
果が過去に得られなかったことだけは付記しておく.
- 33.
まとめ
不均衡データ="各クラスに属するサンプ
ル数に偏りがあるデータ"
不均衡データに対するクラス分類におい
てはいろいろと工夫が必要な場合がある
対応方法としては,正例の誤判別ペナル
ティを調整する方法とサンプリングを工夫
する方法が代表的
個々の問題に応じていろいろと試すべし
- 34.












![> library(kernlab)
> # データの読み込み(データは"../data/"ディレクトリに置いておく)
> abalone <- read.csv("../data/abalone.data", header=FALSE)
> # 19番目のクラスを正例に,それ以外のクラスを負例とする
> label <- abalone[, 9]
> label[label==19] <- "positive"
> label[label!="positive"] <- "negative"
> label <- factor(label)
> table(label)
label
negative positive
4145 32
正例32サンプル,
負例4145サンプルのデータ](https://image.slidesharecdn.com/random-120128040703-phpapp02/85/slide-13-320.jpg)
![> set.seed(123)
> # クロスバリデーションの実行(多項式カーネルを用い,次数は2とする)
> idx <- sample(1:10, nrow(abalone), replace=TRUE)
> for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
+ abalone.test <- abalone[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train, kernel="polydot",
kpar=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+}
> # 予測結果の集計
> table(pred)
pred
negative 全てを負例と判別!!
4177](https://image.slidesharecdn.com/random-120128040703-phpapp02/85/slide-14-320.jpg)




![> label.table <- table(label)
> # 正例の重み(負例と正例のサンプル数の比とする)
> weight.positive <- as.numeric(label.table[1]/label.table[2])
> # 10-fold クロスバリデーションの実行
> for (i in 1:10) { 正例と負例の
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
サンプル数に反比例した
+ abalone.test <- abalone[is.test, -9] ペナルティの重みを指定
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
+ class.weights=c("positive"=weight.positive,
+ "negative"=1),
+ kernel="polydot", kapr=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+ }
> table(label, pred) 何も工夫しないよりは
pred
label negative positive 良くなったが,まだまだ
negative 3118 1027 (モデルパラメータの
positive 19 13 チューニングの余地もまだまだあり)](https://image.slidesharecdn.com/random-120128040703-phpapp02/85/slide-19-320.jpg)



![>idx <- sample(1:10, nrow(abalone.smote), replace=T)
>pred <- rep(NA, nrow(abalone.smote))
># 10-fold クロスバリデーションの実行
>for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone.smote[!is.test, ]
+ abalone.test <- abalone.smote[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
kernel="polydot", kpar=list(degree=2))
+ pred[is.test] <- predict(fit.ksvm, abalone.test)
+}](https://image.slidesharecdn.com/random-120128040703-phpapp02/85/slide-24-320.jpg)
![> # SMOTEでの補間点も含むデータに対する分割表
> table(abalone.smote$label, pred)
negative positive
negative 19 13
positive 1 351
> # 元々のデータに対する分割表
> is.original <- rownames(abalone.smote) %in%
+ rownames(abalone)
> table(abalone.smote[is.original, "label"],
+ pred[is.original])
negative positive
negative 19 13 まだまだチューニングの
positive 0 32 余地はあるが,
それでも精度はかなり
向上](https://image.slidesharecdn.com/random-120128040703-phpapp02/85/slide-25-320.jpg)








