PRML chapter14

1. パターン認識と機械学習
第14章 モデルの統合
D2 大上 雅史
1
PRML輪講 2013/1/7

2. 目次
ベイズモデル平均化
コミッティ
ブースティング
決定木
条件付き混合モデル
1/7/2013 2

3. モデルの統合
複数のモデルを何らかの方法で組み合わせると
単一のモデルより性能が改善することが見込まれる
モデルの結合の枠組みによる手法
• コミッティ(committee), アンサンブル学習(ensemble learning)
• 例：複数のモデルの予測値の平均を予測値とする
• バギング (bagging)
• ブースティング (boosting)
• Random Forest
• 予測に用いるモデルを入力変数の関数とする
• 異なる領域の予測をそれぞれのモデルが担当
• 決定木(decision tree)
• 混合エキスパートモデル
1/7/2013 3

4. 14.1 ベイズモデル平均化
ベイズモデル平均化≠モデルの結合
• 混同されやすい
混合ガウス分布による密度推定の例（でモデルの結合を説明）
• モデルは同時分布 で指定される
• zはデータ点の生成原因がどの混合構成要素であるかを示す
2値の潜在変数(1-of-K符号化)
• 観測変数xについての密度は，潜在変数を周辺化する
• 混合ガウス分布だと次のようになる（モデルの結合の一例）
1/7/2013 4

5. 14.1 ベイズモデル平均化
つづき
• 独立同分布のデータ集合 だと
となり，データ点xnごとに対応する潜在変数znが存在する
h=1,…,Hで番号付けされたいくつかのモデルの
事前確率がp(h)で与えられているとする(ここから違う話)
• データ集合についての周辺分布は次式で与えられる
これはベイズモデル平均化の一例となっている．
1/7/2013 5

6. 14.1 ベイズモデル平均化
hの和の解釈
• 1つのモデルがデータ集合全体の生成を担当
• hの確率分布はどのモデルであるかの不確実性を反映
• データ集合のサイズが大きくなれば不確実性が減少し
事後確率p(h|X)は漸近的に1つのモデルに集中する
まとめ
• ベイズモデル平均化
→単一のモデルからデータ集合全体が生成される
• モデルの結合
→データ点ごとに潜在変数が存在
＝生成原因となるモデル構成要素が異なる
1/7/2013 6

7. 14.1 ベイズモデル平均化
周辺分布以外も同様に議論できる
予測分布 について(演習14.1)
• モデルの集合 を考えると，
ここで
1/7/2013 7

8. 14.1 ベイズモデル平均化
（演習14.1）
事前確率hに潜在変数とパラメータが依存→ベイズモデル平均化
データ点tnごとに潜在変数znが存在→ベイズモデル平均化ではない
1/7/2013 8

9. 14.2 コミッティ
コミッティ
• 複数のモデルを組み合わせて利用することで
単一のモデルを使うよりも性能を改善させる技術
ここでは
「複数のモデルの予測値の平均を予測値とする」
という最も簡単なコミッティ構築について考える
• バイアス要素が小さいモデルの平均化はバリアンスの
寄与がキャンセルされる傾向にある
→正確な予測につながる（3.2節)
1/7/2013 9

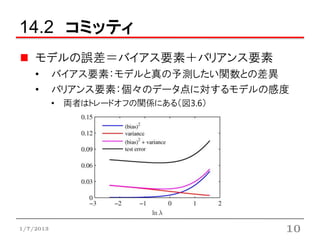
10. 14.2 コミッティ
モデルの誤差＝バイアス要素＋バリアンス要素
• バイアス要素：モデルと真の予測したい関数との差異
• バリアンス要素：個々のデータ点に対するモデルの感度
• 両者はトレードオフの関係にある（図3.6）
1/7/2013 10

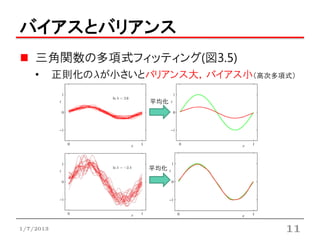
11. バイアスとバリアンス
三角関数の多項式フィッティング(図3.5)
• 正則化の が小さいとバリアンス大，バイアス小（高次多項式）
平均化
平均化
1/7/2013 11

12. バギング
異なる複数のモデルを作るために
• 1つしかないデータ集合から複数のモデルを作りたい
• ブートストラップデータ集合の利用がその方法の1つ
ブートストラップデータ集合の利用
ブートストラップ集約，bagging(bootstrap aggregating)
• M個のブートストラップデータ集合を生成(1.2.3節)
• N点のデータ集合からN点の復元抽出をM回行う
• 個々のデータ集合について予測モデルym(x)を訓練
• コミッティの予測は次で得られる
1/7/2013 12

13. バギングの誤差の評価
真の関数を , モデルとの誤差を とおく
個々のモデルの平均二乗和誤差
個々のモデルの動作から得られる平均誤差
1/7/2013 13

14. バギングの誤差の評価
一方コミッティ予測の二乗誤差の期待値は
1/7/2013 14

15. バギングの誤差の評価
誤差の平均が0で無相関であると仮定する
このとき次が成り立つ（演習14.2）
1/7/2013 15

16. バギングの誤差の評価
バギングのコミッティ誤差について
• 単純にM個の異なるモデルを平均するだけで
モデルの平均誤差を1/Mに低減できる!
• 一見すると衝撃的な結果を示唆．だが．．．
• 個々のモデルの誤差が無相関という仮説に依拠
• 実際には誤差間に高い相関が存在する
→一般的に全体としての誤差の低減効果は小さい
• しかしながらコミッティ誤差について
が成り立つ（次で証明）
1/7/2013 16

17. バギングの誤差の評価
の証明（演習14.3）
• Jensenの不等式を利用（凸関数f に対して）
• 次の対応関係を使う
• こうなる
1/7/2013 17

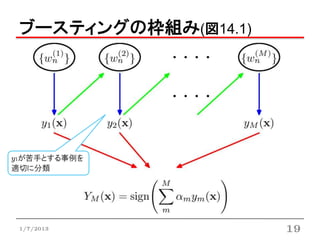
18. 14.3 ブースティング
ブースティング(boosting)
• 複数の「ベース」分類器を統合する手法
（弱学習器, weak learnerとよく呼ばれる）
• バギングとの違い
• 弱学習器を重み付き訓練データによって逐次的に訓練
• 直前の弱学習器の分類結果に基づいて次の重みを調整
• バギングでは独立した訓練データからモデルを学習
• ここでは最も有名なAdaBoostを紹介
• Freund and Schapire, 1996.
• adaptive boostingの略
1/7/2013 18

19. ブースティングの枠組み(図14.1)
y1が苦手とする事例を
適切に分類
1/7/2013 19

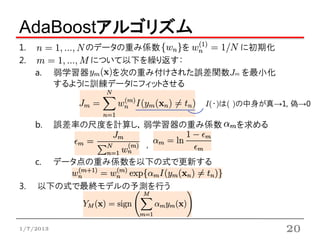
20. AdaBoostアルゴリズム
1. のデータの重み係数 を に初期化
2. について以下を繰り返す：
a. 弱学習器 を次の重み付けされた誤差関数Jm を最小化
するように訓練データにフィットさせる
I(・)は( )の中身が真→1, 偽→0
b. 誤差率の尺度を計算し，弱学習器の重み係数 を求める
,
c. データ点の重み係数を以下の式で更新する
3. 以下の式で最終モデルの予測を行う
1/7/2013 20

21. 弱学習器
弱学習器
• 「弱」とは？
• 正解率がランダム(2値判別なら50%)よりマシという意味
• 別にどんな学習器を使っても良い
• SVM, 決定木, 決定株, 挟み込み型不等式
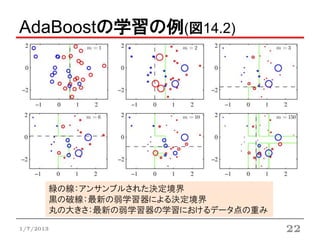
決定株(decision stump)
• 1つの特徴量に対し，ある閾値を超えるか超えないか
で分類する（別名one-level decision tree, 1-rulesなど）
http://en.wikipedia.org/wiki/File:Decision_stump.svg
1/7/2013 21

22. AdaBoostの学習の例(図14.2)
緑の線：アンサンブルされた決定境界
黒の破線：最新の弱学習器による決定境界
丸の大きさ：最新の弱学習器の学習におけるデータ点の重み
1/7/2013 22

23. ブースティングの種類
いろいろなブースティング手法
• AdaBoost (Freud and Shapine, 1996)
• 指数誤差関数（14.3.1で説明）
• ノイズや外れ値に弱い
• LogitBoost (Friedman et al., 1998)
• ロジスティック誤差関数
• AdaBoostよりはノイズや外れ値に強い(?)
• MadaBoost (Domingo and Watanabe, 2000)
• Modified AdaBoost
• ノイズや外れ値に強い
• 変更したけど「まだ」ブースティングの性質を備えているよ
1/7/2013 23

24. 14.3.1 指数誤差の最小化
AdaBoostのデータ点の重み更新式は
指数誤差の逐次的最小化であることを示す
指数誤差関数
• fmはm番目までの弱学習器の線形結合
• tnは訓練集合の目標値 {-1, +1}
1/7/2013 24

25. 14.3.1 指数誤差の最小化
と のパラメータについて誤差関数を最小化
ここでは と が固定されていると
仮定し， のみについて最小化を行う
• 誤差関数を式変形
1/7/2013 25

26. 14.3.1 指数誤差の最小化
で正しく分類されるデータ点集合 ,
残りの誤分類されるデータ点集合を とする
• 正しい分類ではtnとymが同じ→ tnym=1
誤分類ではtnとymは異なる→ tnym=-1
正しい分類 誤分類
誤分類 全体から誤分類を引く
1/7/2013 26

27. 14.3.1 指数誤差の最小化
極小化に関係ない 定数
∴ に関する最小化⇔Jmの最小化(AdaBoost 2-a)
に関する最小化(演習14.6)
• 指数誤差を で微分して0とおく
(AdaBoost 2-b)
1/7/2013 27

28. 14.3.1 指数誤差の最小化
(AdaBoost 2-b)
重みの更新
1/7/2013 28

29. 14.3.1 指数誤差の最小化
を利用して変形
nに関係ない（全てのデータ点を同じ係数で重み付けする）ので無視
(AdaBoost 2-c)
データ点の分類
• 全ての弱学習器の訓練が終わればfMの符号で分類できる
• 1/2を無視して次を得る
(AdaBoost 3)
1/7/2013 29

30. 14.3.2 ブースティングのための誤差関数
指数誤差はこれまで(13章まで)で考えてきた
誤差関数とは異なっている
ここでは指数誤差の性質について考えていく
AdaBoostで用いられる指数誤差の期待損失
1/7/2013 30

31. 14.3.2 ブースティングのための誤差関数
変分最小化（期待損失を汎関数と見て最小化するy(x)を求める）
（演習14.7）
y’(x)が含まれていないのでy(x)で微分する(Euler-Lagrange方程式の第2項が0)
1/7/2013 31

32. 14.3.2 ブースティングのための誤差関数
対数オッズ（の1/2）
AdaBoostは逐次的な最適化戦略という制約の下，
最良の対数オッズ比の近似を，
弱学習器の線形結合による空間内で探索する．
• sign関数の利用の妥当性を示したことになる
1/7/2013 32

33. その他の誤差関数との関係
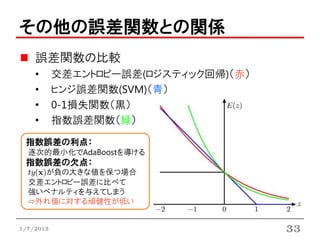
誤差関数の比較
• 交差エントロピー誤差(ロジスティック回帰)（赤）
• ヒンジ誤差関数(SVM)（青）
• 0-1損失関数（黒）
• 指数誤差関数（緑）
指数誤差の利点：
逐次的最小化でAdaBoostを導ける
指数誤差の欠点：
ty(x)が負の大きな値を保つ場合
交差エントロピー誤差に比べて
強いペナルティを与えてしまう
⇨外れ値に対する頑健性が低い
1/7/2013 33

34. 指数誤差の欠点
指数誤差の欠点
• 外れ値に対して頑健性が低い
• 対数尤度関数として解釈できない
• 他クラスの問題に容易に一般化することができない
1/7/2013 34

35. 回帰問題への拡張
二乗和誤差関数を利用
• 新しい弱学習器をそれ以前のモデルの残差
でフィットさせれば良い(演習14.9)
二乗和誤差関数の逐次最小化
以前のモデルの残差
二乗和誤差Eのymに関する最小化→ymを残差にフィットさせる
1/7/2013 35

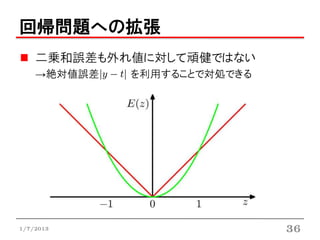
36. 回帰問題への拡張
二乗和誤差も外れ値に対して頑健ではない
→絶対値誤差 を利用することで対処できる
1/7/2013 36

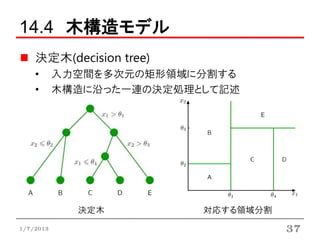
37. 14.4 木構造モデル
決定木(decision tree)
• 入力空間を多次元の矩形領域に分割する
• 木構造に沿った一連の決定処理として記述
決定木 対応する領域分割
1/7/2013 37

38. 決定木
決定木の利点
• 学習が高速
• 人間の可読性が高い
決定木の欠点
• 予測精度がそれほど良くないといわれる
• データ集合の細部に敏感
→訓練データの僅かな変化で分割結果が大きく変わる
• 分割が特徴空間の軸に沿うため準最適となる
• （回帰問題では）境界が不連続な領域ごとの定数の予測
となり, 普通のモデルのような滑らかな関数にならない
1/7/2013 38

39. 決定木
代表的な手法（主に枝刈り基準の違い）
• ID3 (Quinlan, 1979; Quinlan, 1986)：情報利得
• C4.5 (Quinlan, 1993)：情報利得比
• CART (Breiman et al., 1984)：ジニ係数
CART (classification and refression tree)
• 枝刈り基準にジニ係数（Gini index）を利用
1/7/2013 39

40. 参考：The 10 Algorithms in Data Mining
IEEE ICDM2006で
「データマイニングで使われるトップ10アルゴリズム」
という論文が発表された(Wu et al., 2006)
1位 C4.5 6位 PageRank
2位 K-means 7位 AdaBoost
3位 SVM 7位 kNN
4位 Apriori 7位 Naïve Bayes
5位 EMアルゴリズム 10位 CART
1/7/2013 40

41. CART
回帰問題を考える
• 入力変数
• 目標変数 t
• 訓練データ
入力空間の分割が与えられたとき，
二乗和誤差の最小化であれば，
予測変数の最適値は領域内のデータ点tnの平均値（演習14.10）
1/7/2013 41

42. CART
分割の構造の決め方
• 構造の組み合わせが膨大で計算量的に難しい
→単一の根ノードから貪欲最適化する方法が良く用いられる
• 各ステップの処理
• D個の入力変数から分割に用いる変数を選択
• 閾値を設定
• いつノードの追加を終えるのか
• 単純な「残差が一定以下になったら止める」方法はうまくいかない
• 誤差が全然減らないけどそのまま分割を進めていくと誤差が大きく減
るケースなど
• 「葉ノードのデータ点数を規準に木を成長させ，最後に枝刈りする」
1/7/2013 42

43. CART
枝刈りの尺度
• 残差とモデルの複雑さに関する尺度のバランス
枝刈りの方法
• 枝刈り前の木
• 枝刈り後の木
• 葉ノード , 対応する領域
• 領域 に対する最適な予測
1/7/2013 43

44. CART
• 対応する残差の寄与
• 枝刈りの規準
• 正則化パラメータ は交差確認法で選ばれる
1/7/2013 44

45. CART
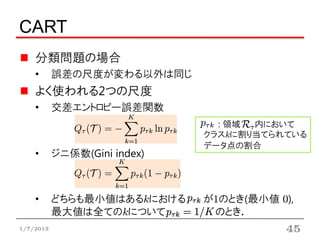
分類問題の場合
• 誤差の尺度が変わる以外は同じ
よく使われる2つの尺度
• 交差エントロピー誤差関数
: 領域 内において
クラスkに割り当てられている
データ点の割合
• ジニ係数(Gini index)
• どちらも最小値はあるkにおける が1のとき(最小値 0),
最大値は全てのkについて のとき．
1/7/2013 45

46. 14.5 条件付き混合モデル
ここでやること
• 決定木では特徴空間の軸に沿ったハードな分割をした
• 各分割において全ての入力変数を考慮した関数による
ソフトな確率的な分割を行うことで緩和できる
• 解釈可能性が犠牲になる
• 葉ノードのモデルを確率的解釈→階層的混合エキスパートモデル
1/7/2013 46

47. 14.5 条件付き混合モデル
順序
• 14.5.1 線形回帰モデルの混合
• 9.2節の混合モデルを条件付きガウス分布に拡張したもの
• 14.5.2 ロジスティックモデルの混合
• 4.3節のロジスティック回帰モデルを混合分布に拡張したもの
• 14.5.3 混合エキスパートモデル
• 混合係数が入力依存に一般化されたもの
• 階層的混合エキスパートモデル
• 混合モデルの各構成要素自体が混合エキスパートモデル
1/7/2013 47

48. 14.5.1 線形回帰モデルの混合
それぞれが重みパラメータwkで支配される
K個の線形回帰モデルを考える
• 目標変数tはとりあえず1次元（拡張→演習14.12）
• 混合係数
• 混合分布は次のように書ける
は をまとめたもの
1/7/2013 48

49. 14.5.1 線形回帰モデルの混合
観測集合 が与えられたときの対数尤度関数
参考：混合ガウスモデル(9章)
1/7/2013 49

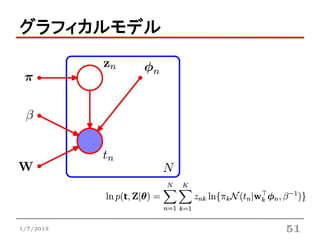
50. 尤度関数最大化
EMアルゴリズムによる尤度関数最大化
• 2値潜在変数集合 を導入
• 完全データに対する対数尤度関数（演習14.13）
1/7/2013 50

51. グラフィカルモデル
1/7/2013 51

52. EMアルゴリズム
Eステップ： を計算する
• 各データ点nに対するクラスkの事後確率(負担率)を求める
• 負担率を用いて事後分布 の下での完全データの
対数尤度の期待値を計算する
1/7/2013 52

53. EMアルゴリズム
Mステップ：関数Qの に関する最大化（ 固定）
• 制約条件 のもと, ラグランジュ未定乗数法より
(演習14.4)
• Qから に依存する項のみ取り出すと
• について微分して0とおく
1/7/2013 53

54. EMアルゴリズム（Mステップ続き）
• Qからwkに依存する項のみ取り出すと
• wkについての微分して0とおく
• 行列表記すると
,
• wkについて解くと
• 式(4.99)のロジスティック回帰の更新式と同じ形
• K=1のときに線形回帰の推定式と一致
1/7/2013 54

55. 人工データ集合の例(図14.8)
2つの線形回帰モデルの混合（赤線と青線）, 下段は負担率
初期値 30回のEM反復計算後 50回のEM反復計算後
1/7/2013 55

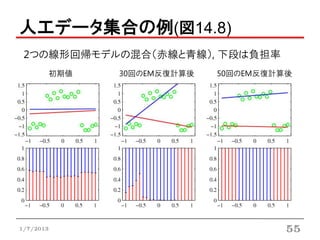
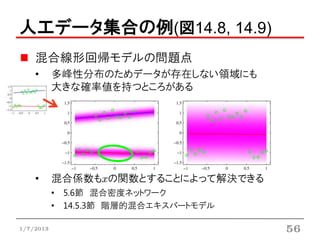
56. 人工データ集合の例(図14.8, 14.9)
混合線形回帰モデルの問題点
• 多峰性分布のためデータが存在しない領域にも
大きな確率値を持つところがある
• 混合係数もxの関数とすることによって解決できる
• 5.6節 混合密度ネットワーク
• 14.5.3節 階層的混合エキスパートモデル
1/7/2013 56

57. 14.5.2 ロジスティックモデルの混合
混合ロジスティック回帰モデル
• ロジスティック回帰モデル(4.3節)の混合モデルver.
• 目標変数の条件付き分布
• 尤度関数
1/7/2013 57

58. 14.5.2 ロジスティックモデルの混合
線形回帰モデルと同様に潜在変数を導入して
EMアルゴリズムで尤度関数最大化を行う
• 完全データの尤度関数
Eステップ：負担率の計算
1/7/2013 58

59. 14.5.2 ロジスティックモデルの混合
Mステップ：Q関数のパラメータに関する最大化
• に関する最大化→いつもの式
• wkに関する最大化→閉じた式にならないので反復計算
• 反復再重み付け最小二乗(IRLS)アルゴリズムなどを利用(4.3.3節)
1/7/2013 59

60. 14.5.2 ロジスティックモデルの混合
• wkについての勾配
• wkについてのヘッセ行列
• データ点に重み がついているだけで
ロジスティック回帰の誤差関数の場合とほぼ同じ形
（式(4.96), (4.97)）
1/7/2013 60

61. 14.5.2 ロジスティックモデルの混合
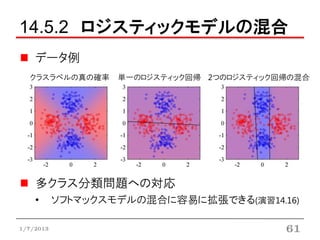
データ例
クラスラベルの真の確率 単一のロジスティック回帰 2つのロジスティック回帰の混合
多クラス分類問題への対応
• ソフトマックスモデルの混合に容易に拡張できる(演習14.16)
1/7/2013 61

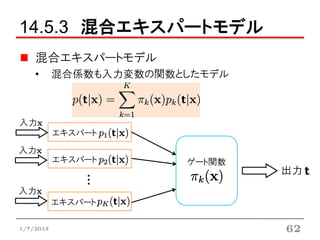
62. 14.5.3 混合エキスパートモデル
混合エキスパートモデル
• 混合係数も入力変数の関数としたモデル
入力x
エキスパート
入力x
エキスパート ゲート関数
出力
・・・
入力x
エキスパート
1/7/2013 62

63. 14.5.3 混合エキスパートモデル
ゲート関数の制約
• 例えば線形ソフトマックスモデルで表現できる
• もしエキスパートも線形モデルならMステップでIRLSを用いた
EMアルゴリズムによってパラメータ推定ができる
1/7/2013 63

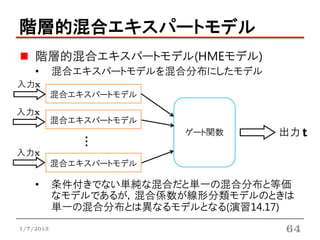
64. 階層的混合エキスパートモデル
階層的混合エキスパートモデル(HMEモデル)
• 混合エキスパートモデルを混合分布にしたモデル
入力x
混合エキスパートモデル
入力x
混合エキスパートモデル
ゲート関数 出力
・・・
入力x
混合エキスパートモデル
• 条件付きでない単純な混合だと単一の混合分布と等価
なモデルであるが，混合係数が線形分類モデルのときは
単一の混合分布とは異なるモデルとなる(演習14.17)
1/7/2013 64

65. 階層的混合エキスパートモデル
EMアルゴリズムにより効率良く最尤推定ができる
変分推論法によるベイズ的扱いが与えられている
決定木の確率的ver.とみなすことができる
• 葉ノードに相当する部分がエキスパートで
入力に応じて各エキスパートの寄与率が決まる
混合密度ネットワークとの比較
• 階層的混合エキスパートモデルの利点
• EMアルゴリズムのMステップの最適化が凸最適化になる
• 混合密度ネットワークの利点
• 構成要素の密度と混合係数をニューラルネットワークの
隠れユニットで共有できる
• 入力空間の分割が非線形にもなり得る
1/7/2013 65