1. 不均衡データのクラス分類
2012年1月28日
第20回Tokyo.R
@sfchaos

2. アジェンダ
 自己紹介
 クラス分類
 不均衡データ
 不均衡データへの対処方法

3. 1. 自己紹介
TwitterID：@sfchaos
お仕事：データ分析

4. 2. クラス分類

5. クラス分類とは，
データの特徴に基づき
データが属するクラスを
推定する問題

6. 例えば，
 スパムメールの判別
 重病の罹患有無の判別

7. クラス分類を行うための手法は
数多く提案されている．
 決定木
 ナイーブベイズ
 サポートベクタマシン
 ブースティング
 ランダムフォレスト etc.

8. クラス分類のアルゴリズムは
一般に多クラスの分類に対応
しかし，今回は2クラスの
分類問題だけを扱う
正例・・・興味のあるクラス
負例・・・興味のないクラス

9. 3. 不均衡データ

10. クラスに属するサンプル数に
偏りがあるデータを
「不均衡データ」と呼ぶ
※英語では"imbalanced data"

11. 現実の問題では，
クラスのサンプル数が
偏っていることは多い
また，興味のあるクラスは
サンプル数が少ないことも多い

12. こうしたデータに対して
工夫もせずに
クラス分類をしようとすると・・・

13. > library(kernlab)
> # データの読み込み(データは"../data/"ディレクトリに置いておく)
> abalone <- read.csv("../data/abalone.data", header=FALSE)
> # 19番目のクラスを正例に，それ以外のクラスを負例とする
> label <- abalone[, 9]
> label[label==19] <- "positive"
> label[label!="positive"] <- "negative"
> label <- factor(label)
> table(label)
label
negative positive
4145 32
正例３２サンプル，
負例４１４５サンプルのデータ

14. > set.seed(123)
> # クロスバリデーションの実行(多項式カーネルを用い，次数は2とする)
> idx <- sample(1:10, nrow(abalone), replace=TRUE)
> for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
+ abalone.test <- abalone[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train, kernel="polydot",
kpar=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+}
> # 予測結果の集計
> table(pred)
pred
negative 全てを負例と判別!!
4177

15. 4. 不均衡データへの
対処方法

16. 不均衡なデータへの対処方法は，
大きく分けて２つある

17. ①正例を誤答したときの
ペナルティを重くする
(cost-sensitive learning)
②正例と負例のサンプル数を
調整する

18. ①正例を誤答したときの
ペナルティを重くする
(cost-sensitive learning)
SVMでは，
ksvm関数(kernlabパッケージ)の
class.weights引数に指定

19. > label.table <- table(label)
> # 正例の重み(負例と正例のサンプル数の比とする)
> weight.positive <- as.numeric(label.table[1]/label.table[2])
> # 10-fold クロスバリデーションの実行
> for (i in 1:10) { 正例と負例の
+ is.test <- idx == i
+ abalone.train <- abalone[!is.test, ]
サンプル数に反比例した
+ abalone.test <- abalone[is.test, -9] ペナルティの重みを指定
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
+ class.weights=c("positive"=weight.positive,
+ "negative"=1),
+ kernel="polydot", kapr=list(degree=2))
+ pred[is.test] <- as.character(predict(fit.ksvm, abalone.test))
+ }
> table(label, pred) 何も工夫しないよりは
pred
label negative positive 良くなったが，まだまだ
negative 3118 1027 (モデルパラメータの
positive 19 13 チューニングの余地もまだまだあり)

20. ②正例と負例のサンプル数を
調整する
 オーバーサンプリング
→正例を増やす
 アンダーサンプリング
→負例を減らす
 両方

21. いろいろなアルゴリズムが
提案されているが，
Rで簡単に試せるのは
DMwRパッケージのSMOTE

22. SMOTEでは，
正例を人工的に作成
(オーバーサンプリング)，
負例をアンダーサンプリングする

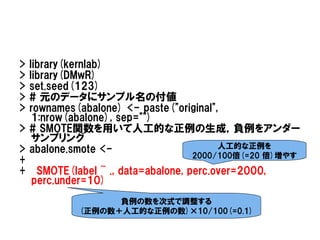
23. > library(kernlab)
> library(DMwR)
> set.seed(123)
> # 元のデータにサンプル名の付値
> rownames(abalone) <- paste("original",
1:nrow(abalone), sep="")
> # SMOTE関数を用いて人工的な正例の生成，負例をアンダー
サンプリング
> abalone.smote <- 人工的な正例を
2000/100倍(=20 倍)増やす
+
+ SMOTE(label ~ ., data=abalone, perc.over=2000,
perc.under=10)
負例の数を次式で調整する
(正例の数＋人工的な正例の数)×10/100(=0.1)

24. >idx <- sample(1:10, nrow(abalone.smote), replace=T)
>pred <- rep(NA, nrow(abalone.smote))
># 10-fold クロスバリデーションの実行
>for (i in 1:10) {
+ is.test <- idx == i
+ abalone.train <- abalone.smote[!is.test, ]
+ abalone.test <- abalone.smote[is.test, -9]
+ fit.ksvm <- ksvm(label ~., data=abalone.train,
kernel="polydot", kpar=list(degree=2))
+ pred[is.test] <- predict(fit.ksvm, abalone.test)
+}

25. > # SMOTEでの補間点も含むデータに対する分割表
> table(abalone.smote$label, pred)
negative positive
negative 19 13
positive 1 351
> # 元々のデータに対する分割表
> is.original <- rownames(abalone.smote) %in%
+ rownames(abalone)
> table(abalone.smote[is.original, "label"],
+ pred[is.original])
negative positive
negative 19 13 まだまだチューニングの
positive 0 32 余地はあるが，
それでも精度はかなり
向上

26. Warning!!
SMOTE関数を使用する際は，
データのクラスラベルは
最後の列に配置しよう
(SMOTE関数が使用している
smoote.exs関数の仕様)
thanks to @dichikaさん

27. またSMOTEがベストな選択とは
限らない
SMOTE以降も様々な手法が
提案されている
Granular SVMなど

28. 最後にランダムフォレストでの
不均衡データへの対処方法に
ついても少しだけ

29. ランダムフォレストの
提案者たちによると，
ランダムフォレストでの
不均衡データへの対応は2つ

30.  Weighted Random Forest
正例，負例をそれぞれ誤って分類する際のペ
ナルティを以下の2箇所で考慮する．
 Gini係数を評価基準として決定木の枝を作成する
とき
 予測ラベルを決定する際に重み付き多数決を取
るとき
 Balanced Random Forest
各ツリーを構築する際, 正例のデータ数と同じ
だけ負例のデータをサンプリングして学習する.

31. RのrandomForestパッケージでは，
 Weighted Random Forest
引数classwtが部分的に対応している模様
(Gini係数のみ？，古いfortranコードを用いて
いる)
 Balanced Random Forest
引数sampsizeに正例と負例に対して同じサ
ンプル数を指定する

32. 引数classwtを調整しても
あまり効果はない?
randomForestパッケージの管理者によると・・・
(http://bit.ly/xJ2mUJ)
現在のclasswtオプションはパッケージが開発された当初から存在しているが，
公式のfortranのコード(バージョン4以降)の実装とは異なる．
クラスの重みを考慮するのは，ノード分割時にGini係数を算出する際のみである．
我々は，クラスの重みをGini係数の算出においてのみ用いても，極端に不均衡
なデータ(例えば1:100やそれ以上)に対してはあまり役に立たないことが分かっ
た．そこで，Breiman教授はクラスの重みを考慮する新しい方法を考案した．こ
の方法は新しいfortranコードに実装されている．
現在のパッケージのclasswtにクラスの重みを指定しても，我々が望んでいた結
果が過去に得られなかったことだけは付記しておく．

33. まとめ
 不均衡データ="各クラスに属するサンプ
ル数に偏りがあるデータ"
 不均衡データに対するクラス分類におい
てはいろいろと工夫が必要な場合がある
 対応方法としては，正例の誤判別ペナル
ティを調整する方法とサンプリングを工夫
する方法が代表的
 個々の問題に応じていろいろと試すべし

34. 参考資料
 Using Random Forest to Learn Imbalanced
Data
 Learning from the imbalanced data