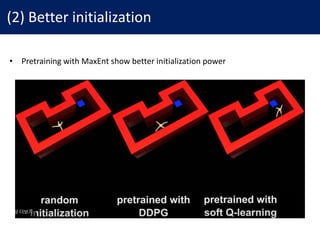
This document discusses reinforcement learning with deep energy-based policies. It motivates using maximum entropy reinforcement learning to find policies that not only maximize reward but also explore possibilities. It presents an approach using energy-based models for the policy and soft Q-learning to find the optimal maximum entropy policy. The method uses neural networks to approximate the soft Q-function and a sampling network to draw samples from the policy. Experiments show maximum entropy policies provide better exploration, initialization, compositionality and robustness compared to deterministic policies.

1. Reinforcement Learning with
Deep Energy-Based Policies
2017.10.11.
Sangwoo Mo

2. Motivation
• In standard RL, the optimal policy is deterministic;
𝜋"#$
∗
𝑎 𝑠 = argmax. 𝑄(𝑠, 𝑎)
• However, 𝜋"#$
∗
finds the best single path, which may leads several problems
• For example, it is not robust to the changing environment
• It motivates the policy not only maximize reward, but also explore possibilities
• => maximize entropy of actions

3. Maximum Entropy RL
• maximum entropy policy:
𝜋3.456# = argmax7 8 𝔼 ":,.: ~<=
[𝑟 𝑠#, 𝑎# + 𝛼 ℋ(⋅ |𝑠#)]
#
• In this paper, we consider continuous state/action space
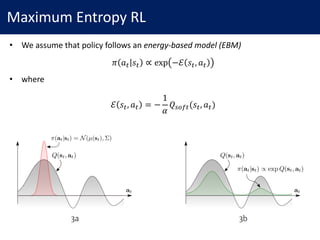
• We assume that policy follows an energy-based model (EBM)
𝜋 𝑎# 𝑠# ∝ exp −ℰ 𝑠#, 𝑎#
• where
ℰ 𝑠#, 𝑎# = −
1
𝛼
𝑄"NO#(𝑠#, 𝑎#)

4. Maximum Entropy RL
• We assume that policy follows an energy-based model (EBM)
𝜋 𝑎# 𝑠# ∝ exp −ℰ 𝑠#, 𝑎#
• where
ℰ 𝑠#, 𝑎# = −
1
𝛼
𝑄"NO#(𝑠#, 𝑎#)

5. Relation to Soft Q-learning
• As the analogy of standard RL, define
𝑄"NO#
∗
𝑠#, 𝑎# = 𝑟# + 𝔼 ":PQ,…, ∼<=
8 𝛾U
V
UWX
𝑟#YU + 𝛼 ℋ 𝜋3.456#
∗
⋅ 𝑠#YU
𝑉"NO#
∗
𝑠# = 𝛼 log ] exp
1
𝛼
𝑄"NO#
∗
(𝑠#, 𝑎^) 𝑑𝑎^
`
• Theorem 1. The optimal MaxEnt policy is
𝜋3.456#
∗
𝑎# 𝑠# = exp
1
𝛼
𝑄"NO#
∗
𝑠#, 𝑎# − 𝑉"NO#
∗
𝑠#
• Theorem 2. The soft Q-function satisfies the soft Bellman equation
𝑄"NO#
∗
𝑠#, 𝑎# = 𝑟# + 𝛾𝔼":PQ∼ab
[𝑉"NO#
∗
𝑠#YX ]

6. Soft Q-Iteration
• Thus, we can find MaxEnt policy by soft Q-learning
• As Q-iteration, we can obtain 𝑄"NO#
∗
and 𝑉"NO#
∗
by soft Q-iteration
• Theorem 3. With mild condition1, the iteration converges to 𝑄"NO#
∗
and 𝑉"NO#
∗
𝑄"NO#
𝑠#, 𝑎# ← 𝑟# + 𝛾𝔼":PQ∼ab
𝑉"NO#
𝑠#YX , ∀𝑠#, 𝑎#
𝑉"NO#
𝑠# ← 𝛼 log ] exp
1
𝛼
𝑄"NO#
(𝑠#, 𝑎^) 𝑑𝑎^
`
, ∀𝑠#
• However, there are some challenges for this algorithm
1. Computing soft value function 𝑉"NO#
𝑠# is intractable
2. Sampling from policy function 𝜋3.456#
𝑎# 𝑠# is intractable
1. 𝑄"NO#, 𝑉"NO# are bounded, ∫ exp
X
f
𝑄"NO# ⋅, 𝑎^
𝑑𝑎′`
< ∞, 𝑄"NO#
∗
< ∞ exisits

7. (1) Computing soft value function
• Similar to DQN, use parametrized model 𝑄"NO#
j
𝐽l 𝜃 = 𝔼":~nb:
, .:~no:
1
2
𝑄q"NO#
jr
𝑠#, 𝑎# − 𝑄"NO#
j
𝑠#, 𝑎#
s
• where
𝑄q"NO#
j
= 𝑟# + 𝛾𝔼":PQ∼ab
𝑉"NO#
j
𝑠#YX
• and 𝜃̅ is parameter of target network and
𝑉"NO#
j
𝑠#YX = 𝛼 log 𝔼nou
exp 1/𝛼 𝑄"NO#
j
𝑠#YX, 𝑎^
𝑞.u(𝑎^)
• We can use arbitrary 𝑞":
, 𝑞.:
, but typical choice is samples from current policy

8. (2) Sampling from policy function
• Since MCMC is not tractable for online, we use sampling network
𝑓y 𝜉; 𝑠# ∼ 𝜋y ⋅ 𝑠#
• that maps random noise to policy EBM
• cf) 𝜋y ⋅ 𝑠# can be views as a critic for actor-critic algorithm
• Find 𝜙 that minimize
𝐽7 𝜙; 𝑠# = 𝐷~• 𝜋y ⋅ 𝑠# ∥ 𝜋j ⋅ 𝑠#
= 𝐷~• 𝜋y ⋅ 𝑠# ∥ exp
1
𝛼
𝑄"NO#
j
𝑠#, 𝑎# − 𝑉"NO#
j
𝑠#
• To solve the problem, we use SVGD (Stein Variational Gradient Descent)

9. (2) Sampling from policy function
• ∆𝑓y is the optimal direction in RKHS of 𝜅 (typically Gaussian kernel)
∆𝑓y ⋅ ; 𝑠# = 𝔼.:~7ƒ[𝜅 𝑎#, 𝑓y ⋅ ; 𝑠# 𝛻.u 𝑄"NO#
j
𝑠#, 𝑎# …
.uW.:
+𝛼 𝛻.u 𝜅 𝑎^, 𝑓y ⋅ ; 𝑠# …
.uW.:
]
• We can compute the gradient 𝜕𝐽/𝜕𝜙 with ∆𝑓y
𝜕𝐽7 𝜙; 𝑠#
𝜕𝜙
∝ 𝔼‡ ∆𝑓y 𝜉; 𝑠#
𝜕𝑓y(𝜉; 𝑠#)
𝜕𝜙
• Putting (1) and (2), we can implement soft Q-learning

10. Experiment
• MaxEnt policy has 4 advantages compare to standard RL
1. Better exploration
2. Better initialization
3. Compositionality
4. Robustness
• Compare MaxEnt to deterministic policy (DDPG + noise)
• Mostly qualitative than quantitative

11. (1) Better exploration
• DDPG only explores upper/lower half w.r.t. random seed,
but MaxEnt explores both upper/lower side during training

12. (2) Better initialization
• reward = speed (any direction)
• For pretrained policy, DDPG goes to one direction, but MaxEnt spreads out

13. (2) Better initialization
• Pretraining with MaxEnt show better initialization power

14. (3) Compositionality
• Let 𝑄X and 𝑄s be the optimal soft q-function for 𝑟X and 𝑟s
• Then 𝑄X + 𝑄s is becomes the optimal soft q-function 𝑟X + 𝑟s

15. (4) Robustness
• While DDPG breaks for unexpected interruption, MaxEnt recovers

16. Demo
https://sites.google.com/view/softqlearning/home