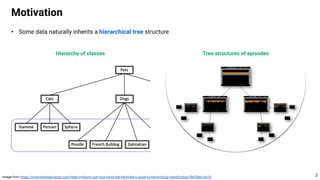
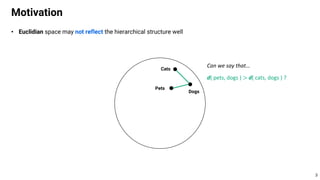
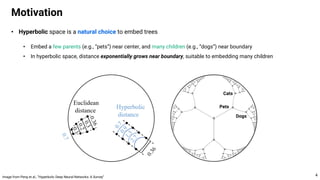
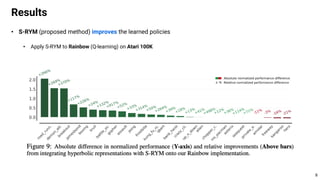
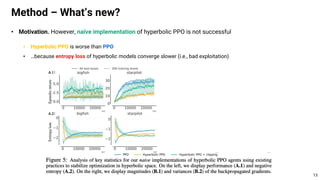
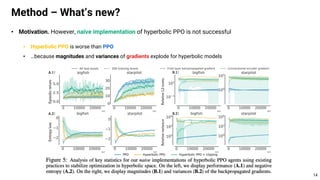
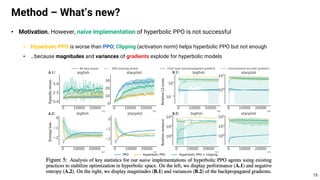
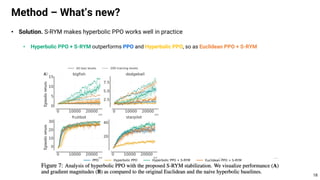
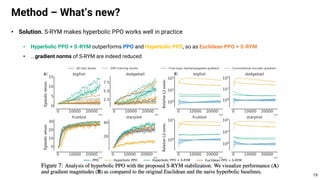
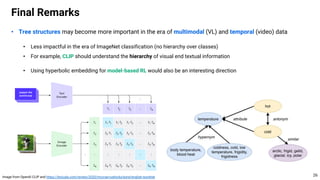
This document proposes using hyperbolic space to embed hierarchical tree structures, like those that can represent sequences of events in reinforcement learning problems. Specifically, it suggests a method called S-RYM that applies spectral normalization to regularize gradients when training deep reinforcement learning agents with hyperbolic embeddings. This stabilization technique allows naive hyperbolic embeddings to outperform standard Euclidean embeddings. It works by reducing gradient norm explosions during training, allowing the entropy loss to converge properly. The document provides technical details on spectral normalization, hyperbolic space representations, and how S-RYM trains deep reinforcement learning agents with stabilized hyperbolic embeddings.

1. 2023.02.22.
Sangwoo Mo
1

2. • Some data naturally inherits a hierarchical tree structure
Motivation
2
Image from https://towardsdatascience.com/https-medium-com-noa-weiss-the-hitchhikers-guide-to-hierarchical-classification-f8428ea1e076
Hierarchy of classes Tree structures of episodes

3. • Euclidian space may not reflect the hierarchical structure well
Motivation
3
Pets
Cats
Dogs
Can we say that…
d( pets, dogs ) > d( cats, dogs ) ?

4. • Hyperbolic space is a natural choice to embed trees
• Embed a few parents (e.g., “pets”) near center, and many children (e.g., “dogs”) near boundary
• In hyperbolic space, distance exponentially grows near boundary, suitable to embedding many children
Motivation
4
Image from Peng et al., “Hyperbolic Deep Neural Networks: A Survey”
Pets
Dogs
Cats

5. • Why I choose this paper?
• Interpreting a sequence (e.g., episode, video) as a tree is an interesting and useful idea
• It is the first paper to make hyperbolic embedding to work in RL
• Contributions
• The concept of hyperbolic space is appealing… but was not successful in practice
• It is mostly due to an optimization issue, and a simple regularization trick makes it work well
• Trick. Reduce the gradient norm of NN
(apply spectral normalization (SN) and then rescaling outputs)
TL;DR
5

6. • Episodes moves from the root (center) to leaves (boundary) as the agent progresses
• Green lines (good policy) moves from the center to boundary
• Red lines (random policy) moves to random directions
• Hyperbolic embeddings give a natural explanations for the RL agents
Results
6

7. • S-RYM (proposed method) improves the learned policies
• Apply S-RYM to PPO (policy gradient) on Procgen
• Reducing embedding dim to 32 improves the performance (hyperbolic space more efficiently embeds episodes)
Results
7

8. • S-RYM (proposed method) improves the learned policies
• Apply S-RYM to Rainbow (Q-learning) on Atari 100K
Results
8

9. • Motivation. Deep RL policies already makes the embeddings to be hyperbolic
• Return (both train -- and test –) increases as 𝜹-hyperbolicity decreases
Method – What’s new?
9

10. • Motivation. Deep RL policies already makes the embeddings to be hyperbolic
• Return (both train -- and test –) increases as 𝜹-hyperbolicity decreases
• Gap (of train -- and test –) enlarges when 𝜹-hyperbolicity shows U-curve
Method – What’s new?
10

11. • Motivation. Deep RL policies already makes the embeddings to be hyperbolic
• Return (both train -- and test –) increases as 𝜹-hyperbolicity decreases
• Gap (of train -- and test –) enlarges when 𝜹-hyperbolicity shows U-curve
Method – What’s new?
11
𝜹-hyperbolicity
See https://en.wikipedia.org/wiki/Hyperbolic_metric_space for detailed explanations for 𝛿-hyperbolicity

12. • Motivation. However, naïve implementation of hyperbolic PPO is not successful
• Hyperbolic PPO is worse than PPO
• Return of hyperbolic models are worse than PPO
Method – What’s new?
12

13. • Motivation. However, naïve implementation of hyperbolic PPO is not successful
• Hyperbolic PPO is worse than PPO
• …because entropy loss of hyperbolic models converge slower (i.e., bad exploitation)
Method – What’s new?
13

14. • Motivation. However, naïve implementation of hyperbolic PPO is not successful
• Hyperbolic PPO is worse than PPO
• …because magnitudes and variances of gradients explode for hyperbolic models
Method – What’s new?
14

15. • Motivation. However, naïve implementation of hyperbolic PPO is not successful
• Hyperbolic PPO is worse than PPO; Clipping (activation norm) helps hyperbolic PPO but not enough
• …because magnitudes and variances of gradients explode for hyperbolic models
Method – What’s new?
15

16. • Solution. Apply spectral normalization (SN) to regularize the gradient norms
• SN normalizes the weights 𝑾 to have spectral norm (largest singular value) 𝝈 𝑾 ≈ 𝟏
• It regularizes the gradients neither explode nor vanish (updated in the normalized weight space)
• S-RYM (spectrally-regularized hyperbolic mappings) applies SN to all layers except the final hyperbolic layer
Method – What’s new?
16
Miyato et al. “Spectral Normalization for Generative Adversarial Networks,” ICLR 2018.
Image from https://blog.ml.cmu.edu/2022/01/21/why-spectral-normalization-stabilizes-gans-analysis-and-improvements/
Transform to
hyperbolic embedding

17. • Solution. Apply spectral normalization (SN) to regularize the gradient norms
• SN normalizes the weights 𝑾 to have spectral norm (largest singular value) 𝝈 𝑾 ≈ 𝟏
• It regularizes the gradients neither explode nor vanish (updated in the normalized weight space)
• S-RYM (spectrally-regularized hyperbolic mappings) applies SN to all layers except the final hyperbolic layer
• However, to maintain the overall scale of activations, it rescales the activations by 𝑛 (embedding dim)
• If 𝑧 ∈ ℝ! follows Gaussian distribution, 𝑧 follows scaled Chi distribution 𝒳! and 𝔼 𝑧 ≈ 𝑛
Method – What’s new?
17
Miyato et al. “Spectral Normalization for Generative Adversarial Networks,” ICLR 2018.
Image from https://blog.ml.cmu.edu/2022/01/21/why-spectral-normalization-stabilizes-gans-analysis-and-improvements/
× 𝒏𝟏 × 𝒏𝟐
Transform to
hyperbolic embedding

18. • Solution. S-RYM makes hyperbolic PPO works well in practice
• Hyperbolic PPO + S-RYM outperforms PPO and Hyperbolic PPO, so as Euclidean PPO + S-RYM
Method – What’s new?
18

19. • Solution. S-RYM makes hyperbolic PPO works well in practice
• Hyperbolic PPO + S-RYM outperforms PPO and Hyperbolic PPO, so as Euclidean PPO + S-RYM
• ...gradient norms of S-RYM are indeed reduced
Method – What’s new?
19

20. • Spectral normalization (SN)
• Normalize the weights as 𝑾/𝝈(𝑾) at forward time… but how to compute the spectral norm 𝝈(𝑾)?
• A. Apply power iteration!
Method – Technical details
20

21. • Spectral normalization (SN)
• Power iteration finds the largest singular value by iterating
• Why it works?
• 𝑏" converges to the singular vector 𝑣# and thus can find the corresponding (largest) singular value 𝜆#
Method – Technical details
21
See https://en.wikipedia.org/wiki/Power_iteration

22. • Hyperbolic embedding
• Recent hyperbolic models follow the standard Euclidean embeddings for all layers
except converting the final embedding 𝐱$ = 𝑓$(𝐱) to the hyperbolic embedding 𝐱%
Method – Technical details
22

23. • Hyperbolic embedding
• Recent hyperbolic models follow the standard Euclidean embeddings for all layers
except converting the final embedding 𝐱$ = 𝑓$(𝐱) to the hyperbolic embedding 𝐱%
• Specifically, 𝐱% is given by an exponential map 𝐱% = exp𝟎(𝐱$) from the origin 𝟎 using the velocity 𝐱$
• Exponential map is a projection of a (local tangent) vector 𝑋𝑌 to the manifold 𝑀
Method – Technical details
23
Image from https://www.researchgate.net/figure/An-exponential-map-exp-X-TX-M-M_fig1_224150233

24. • Hyperbolic embedding
• Hyperbolic space have several coordinate systems
• Similar to Euclidean space has Cartesian, spherical, or etc. systems
• How to represent the hyperbolic space is another research topic, but S-RYM uses Poincaré ball
Method – Technical details
24
Image from https://en.wikipedia.org/wiki/Coordinate_system

25. • Hyperbolic embedding
• In Poincaré ball, the operations (to compute the final output) are given by:
• Exponential map (from origin):
• Addition (of two vectors):
• Distance (from a generalized hyperplane parametrized by 𝐩 and 𝐰 ):
• S-RYM computes the final policy/value scalars 𝑓% 𝐱% = 𝑓'(𝐱%) '∈) for all (discrete) actions 𝑖 ∈ 𝐴
Method – Technical details
25
Image from https://en.wikipedia.org/wiki/Coordinate_system

26. • Tree structures may become more important in the era of multimodal (VL) and temporal (video) data
• Less impactful in the era of ImageNet classification (no hierarchy over classes)
• For example, CLIP should understand the hierarchy of visual end textual information
• Using hyperbolic embedding for model-based RL would also be an interesting direction
Final Remarks
26
Image from OpenAI CLIP and https://lexicala.com/review/2020/mccrae-rudnicka-bond-english-wordnet

27. Thank you for listening! 😀
27