More Related Content
PPTX
PPTX
PPTX
PDF
PPTX
PDF
PPTX
PPTX
What's hot
PPTX
強化学習の基礎と深層強化学習(東京大学 松尾研究室 深層強化学習サマースクール講義資料) PDF
PPTX
PDF
[DL輪読会]Temporal Abstraction in NeurIPS2019 PPTX
PDF
[DL輪読会]深層強化学習はなぜ難しいのか?Why Deep RL fails? A brief survey of recent works. PDF
SSII2021 [TS2] 深層強化学習 〜 強化学習の基礎から応用まで 〜 PDF
PDF
PPTX
PPTX
PPTX
PPTX
PPTX
【DL輪読会】Reward Design with Language Models PDF
PPTX
PDF
クラシックな機械学習の入門 6. 最適化と学習アルゴリズム PDF
PDF
Introduction to A3C model PDF
Similar to 強化学習4章
PDF
PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning PDF
PPTX
Reinforcement Learning(方策改善定理) PDF
PPTX
【DL輪読会】Is Conditional Generative Modeling All You Need For Decision-Making? PDF
PDF
PDF
PDF
PDF
PDF
確率的深層学習における中間層の改良と高性能学習法の提案 PDF
PDF
NIPS KANSAI Reading Group #7: Temporal Difference Models: Model-Free Deep RL ... DOCX
PPTX
【最新ではありません。再度URL送付しています→https://www.slideshare.net/ssuserf4860b/day-250965207... PPTX
[Oracle Code Night] Reinforcement Learning Demo Code PDF
Computational Motor Control: Reinforcement Learning (JAIST summer course) PPTX
データサイエンス勉強会~機械学習_強化学習による最適戦略の学習 PDF
More from hiroki yamaoka
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
強化学習4章
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
Editor's Notes
- #8 標本近似の妥当性
近似作用素が真の作用素に収束することが言いたい
- #9 エルゴード性:各状態の滞在確率の極限は初期状態に依存しない










![15
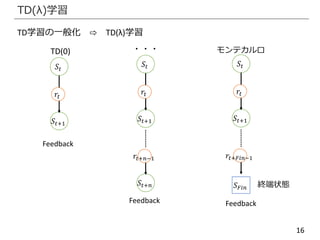
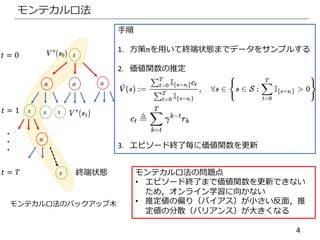
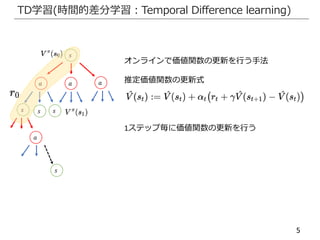
TD学習
[入力] S,Aは既知.行動の入力に対して次状態と報酬を出力するモデル.
π,γ,α,終了条件.
[出力] 方策πの推定価値関数
1. 初期化
推定価値関数を任意に初期化・t=0に初期化・初期状態𝑠0を観測
2. 環境との相互作用
方策 に従い行動𝑎 𝑡を選択し環境に入力,環境から報酬𝑟𝑡と次状態𝑠𝑡+1を観測
3. 学習
TD誤差を計算
推定価値関数を更新
4. 終了判定
終了条件を満たしていれば終了
それ以外は手順2から繰り返す](https://image.slidesharecdn.com/rlchapter4-200826105716/85/4-15-320.jpg)