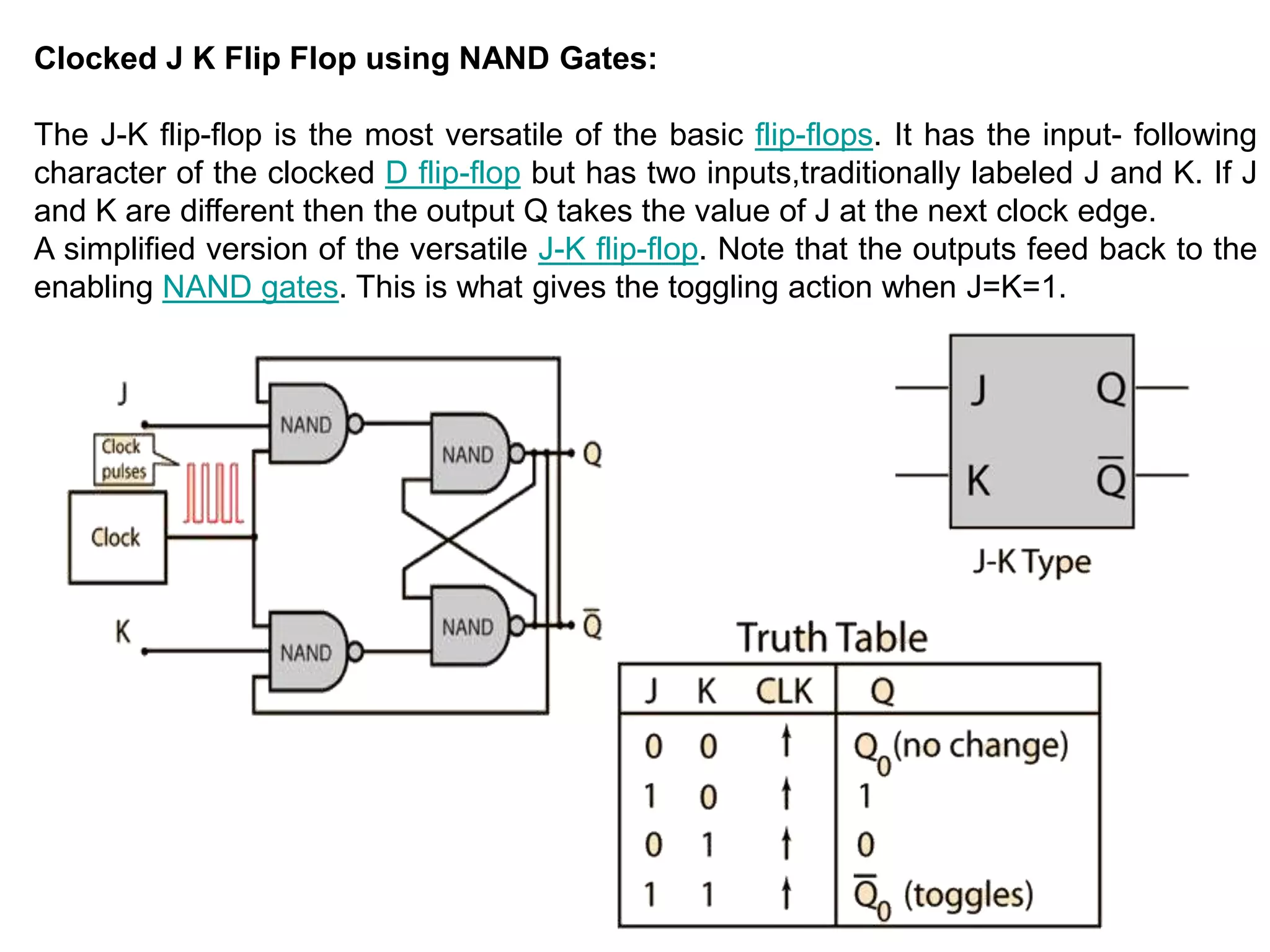
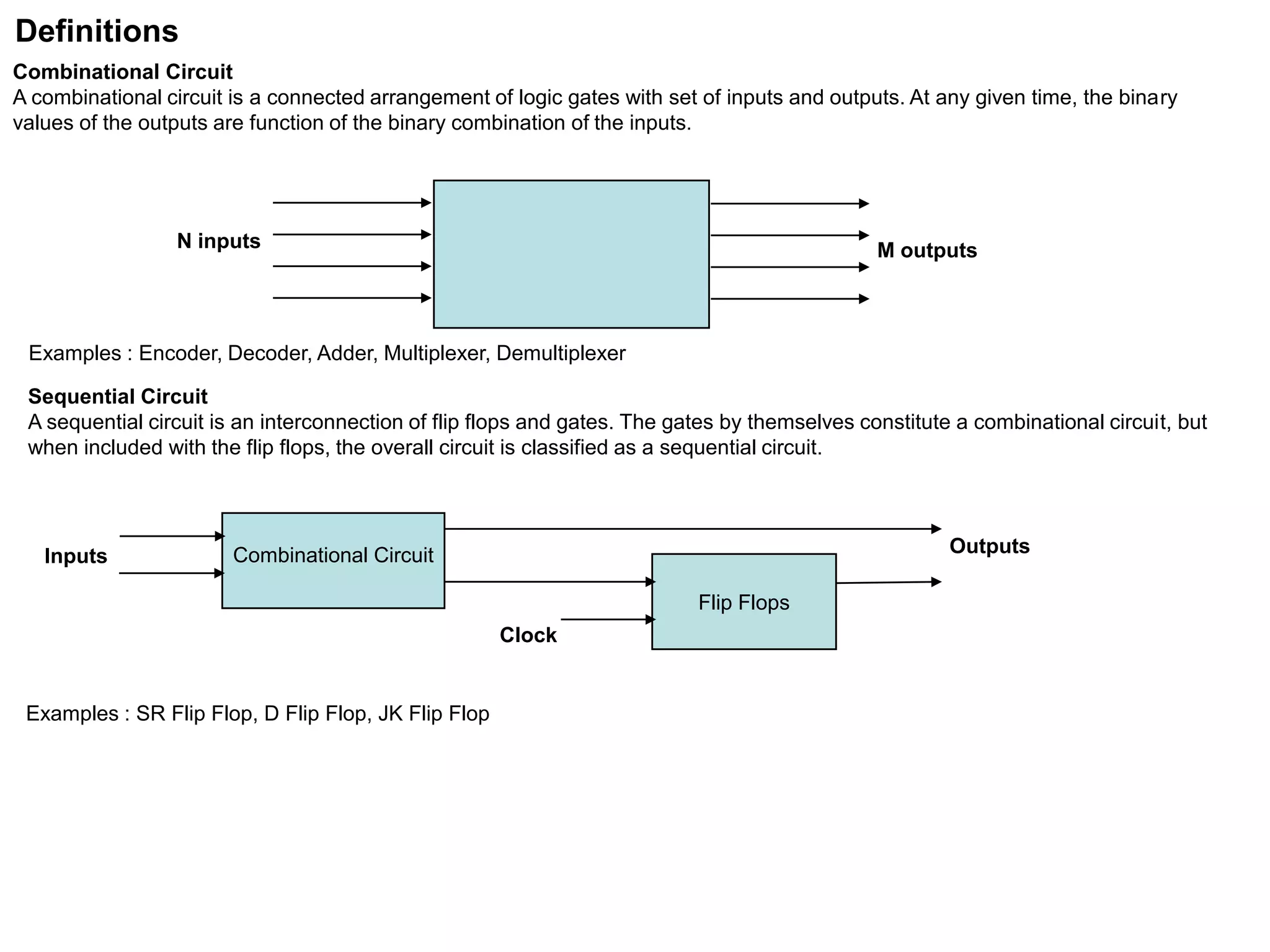
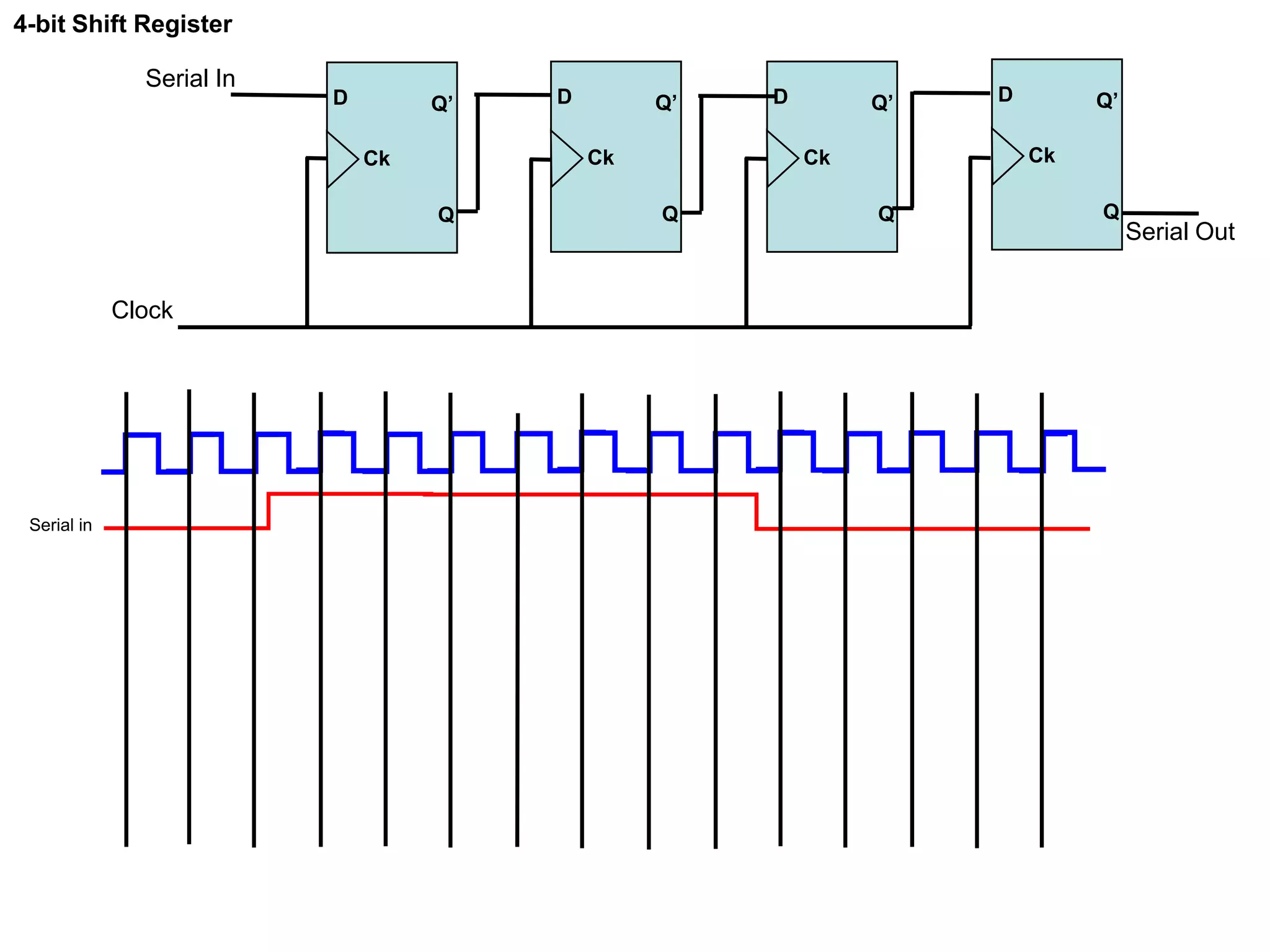
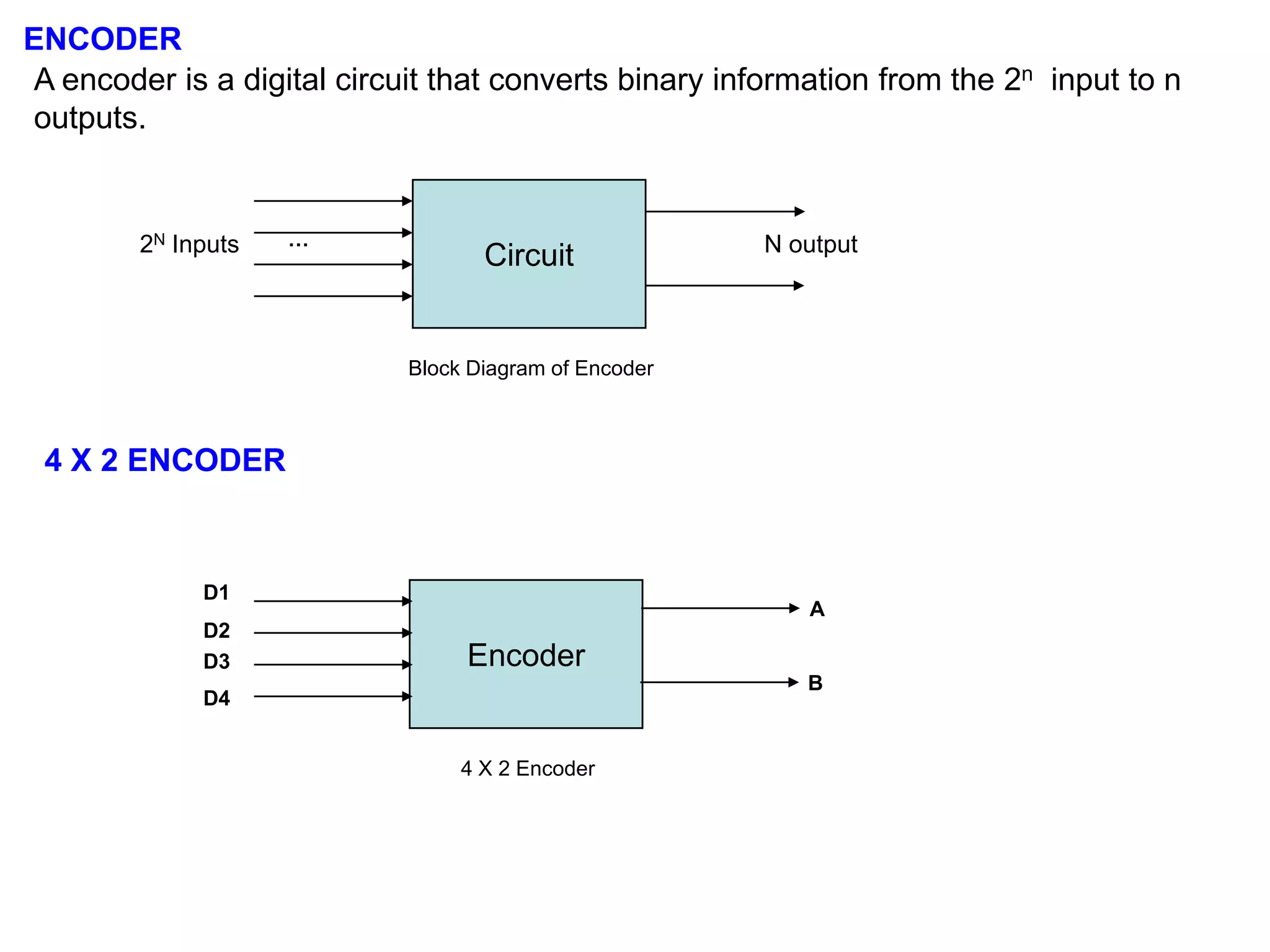
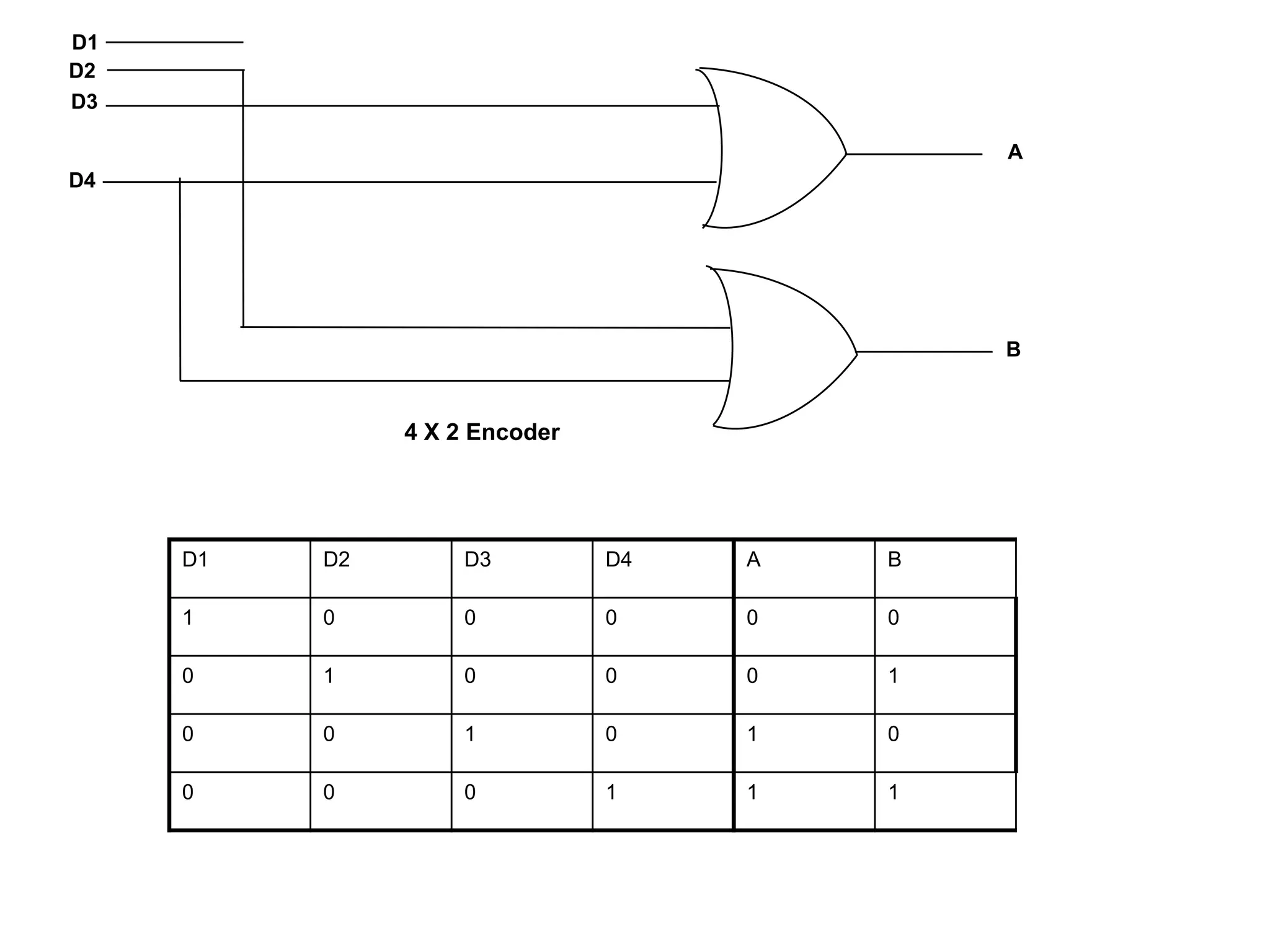
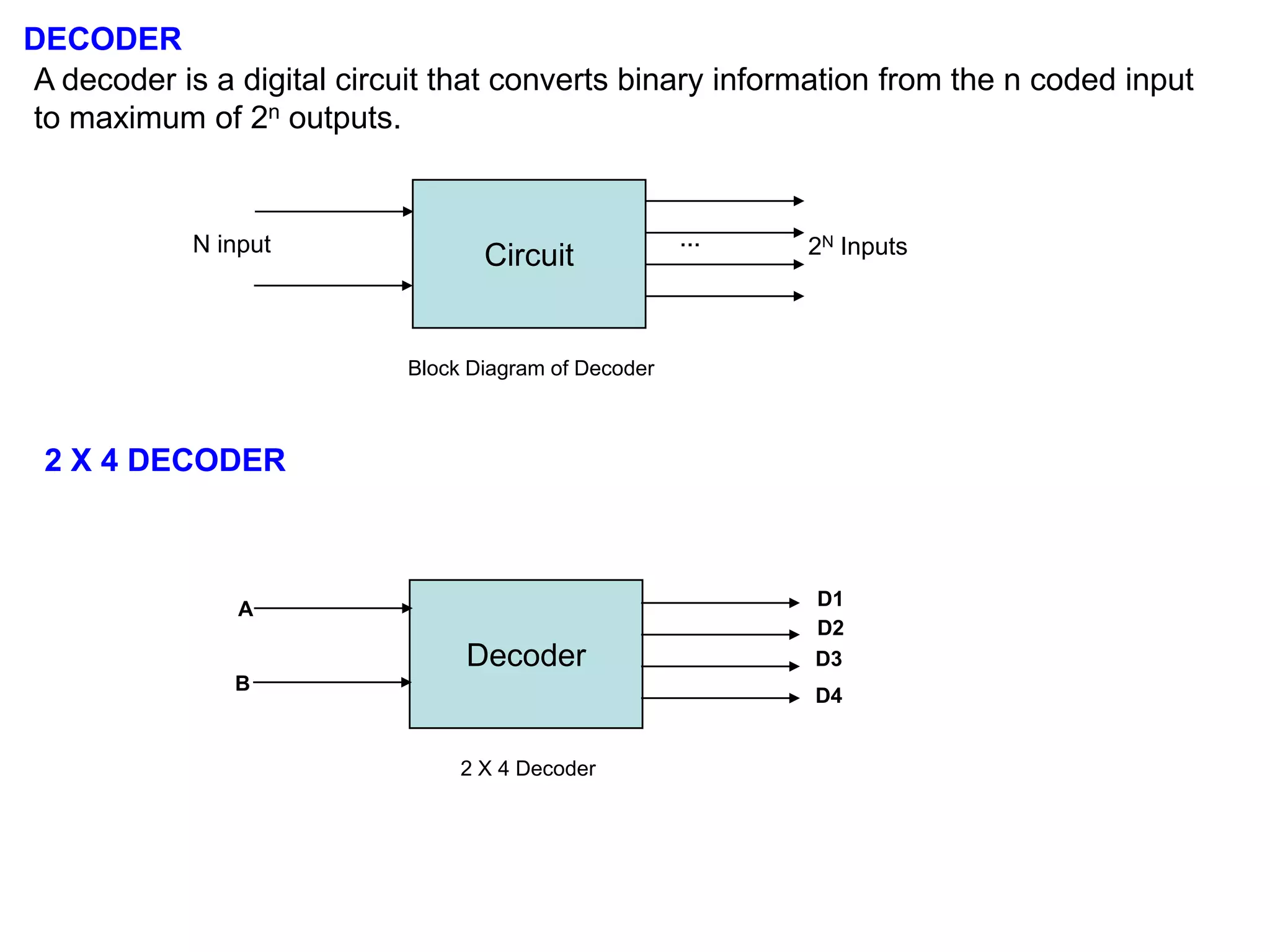
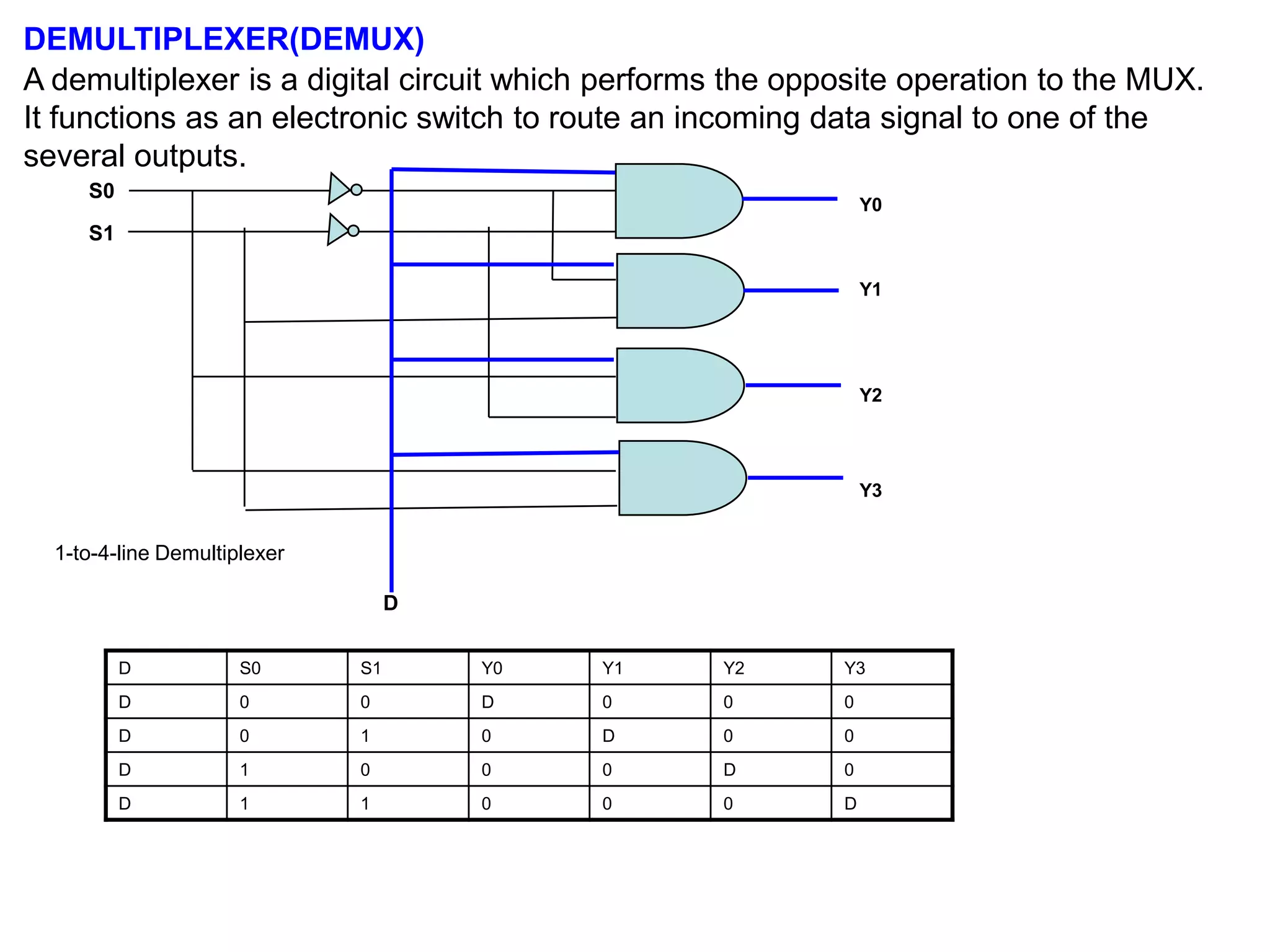
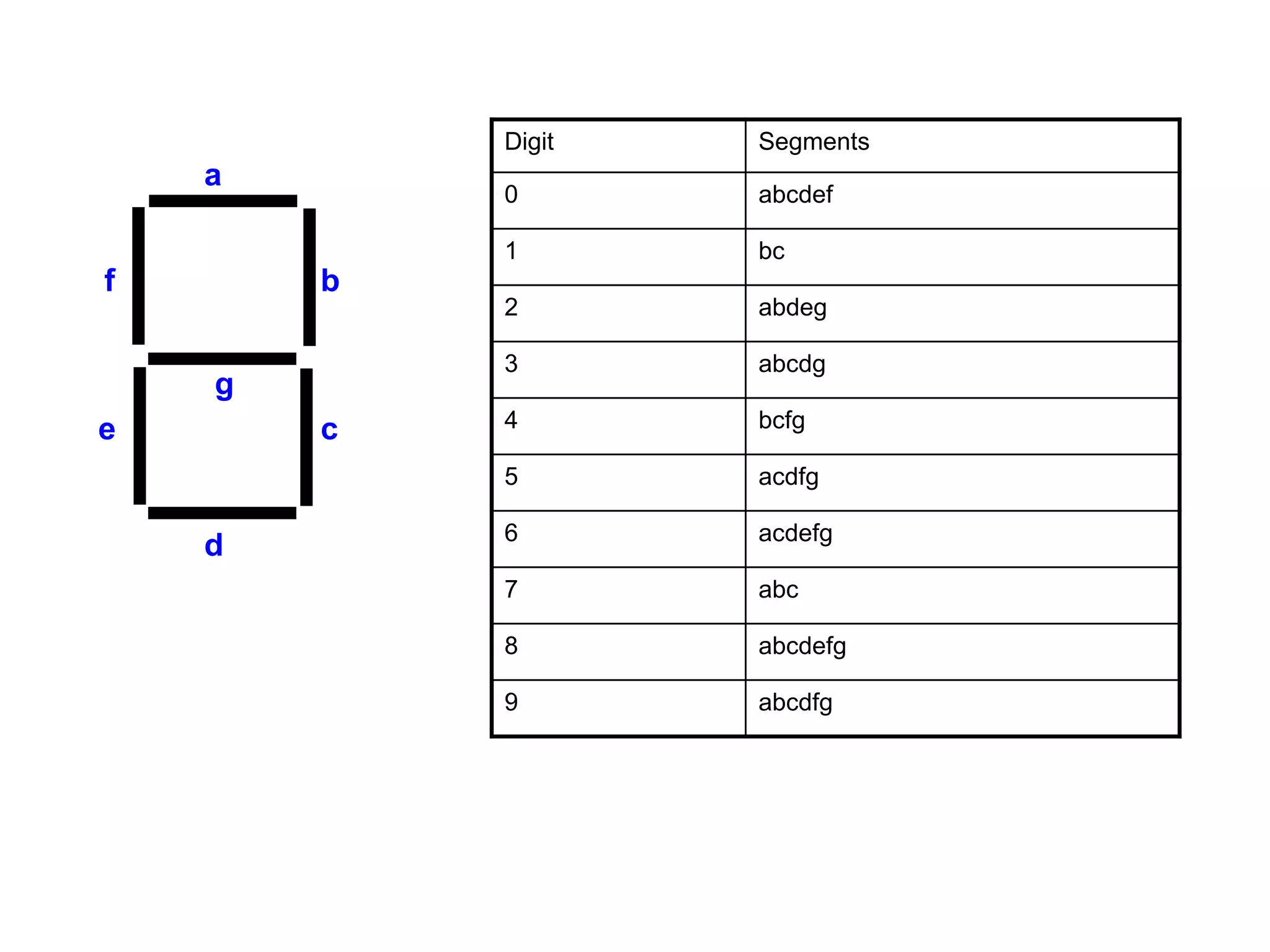
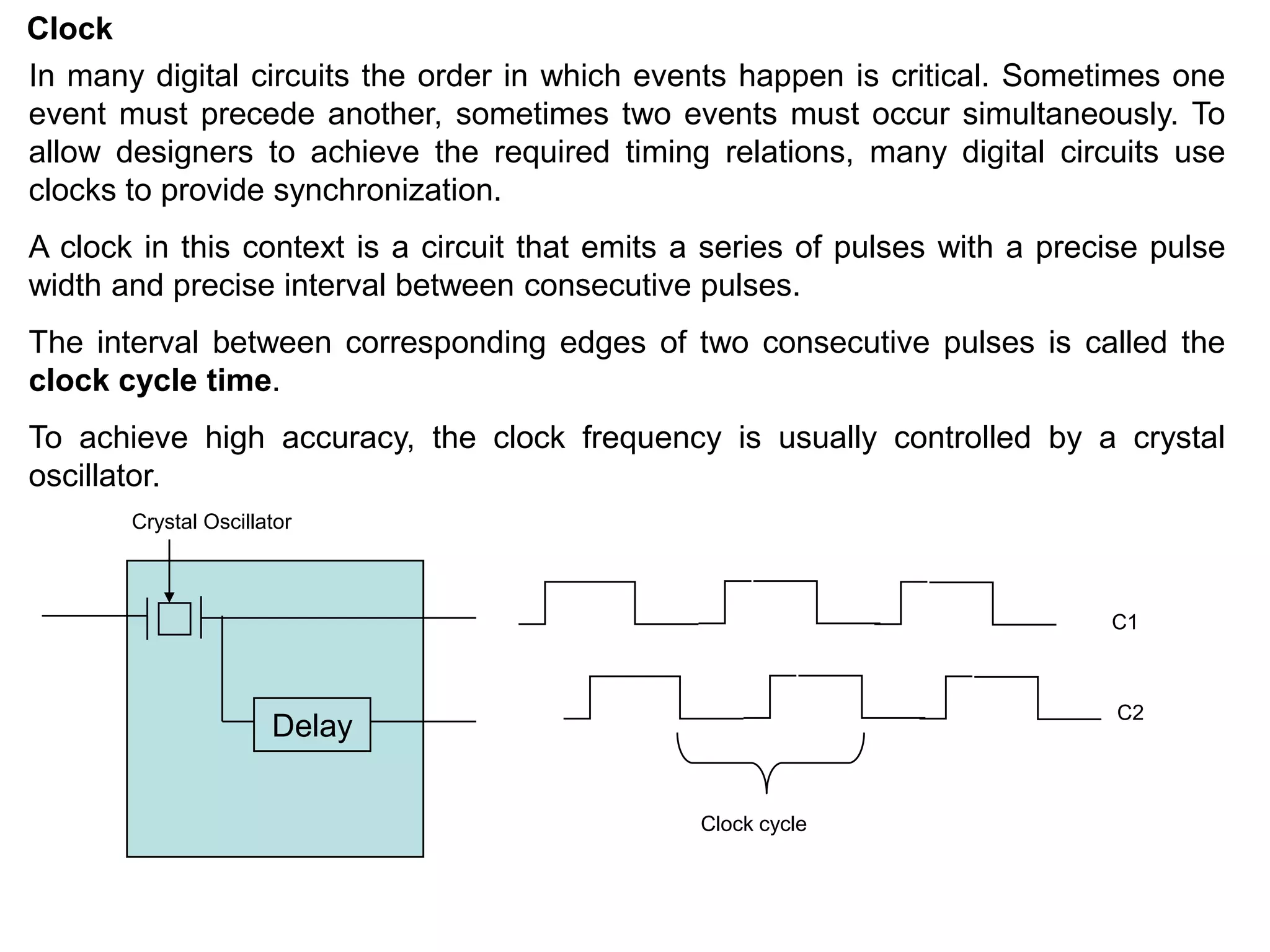
This document provides information about various digital circuits including half adder, full adder, encoder, decoder, multiplexer, demultiplexer, seven segment display circuit, clock, flip flop, integrated circuit and more. It defines combinational and sequential circuits. It describes half adder, full adder, encoder, decoder, multiplexer, demultiplexer and seven segment display circuits. It also explains clock, flip flops including SR, D, JK flip flops, integrated circuits and definitions.

1. Course : AIT 204
Course Title : Computer Organization and Architecture (COA)
Course Credits : 3 + 0
Course Teacher : Dr. Y R Ghodasara & Prof. K. C. Kamani
College of Agricultural Information Technology
Anand Agricultural University
Anand
Unit II

2. HALF ADDER
A digital circuit that performs the arithmetic addition of two bits is called half adder.
1-bit addition
0
+0
---
0
0
+1
---
01
1
+0
---
01
1
+1
---
10
1
1
-
0
1Carry
A
B
Circuit
A
B
Sum
Carry
Block Diagram of Half Adder

3. 0 1
1 0
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
SUM
A B
0 1
1
1
Rectangle 1
A B
0 1
R1=A’B
Rectangle 2
A B
1 0
R2=AB’
SUM = R1 + R2
= A’B+AB’
0 0
0 1
CARRY
A B
0 1
1
1
Rectangle 1
A B
1 1
R1=AB
A’BA
SUM
B
B’
AB’
A’
CARRY
Half Adder Circuit

4. FULL ADDER
A digital circuit that performs the arithmetic addition of multiple bits is called a full
adder.
2-bit addition
00
+10
---
10
10
+10
---
100
11
+01
---
100
11
+11
---
110
1
1
-
0
1
1
-
1
1Carry
1Carry
A
B
Circuit
A
B
Cin
Sum
Cout
Block Diagram of Full Adder

5. Full Adder
Cout
Sum
Cin
A
B
A B Cin Sum Cout
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

6. ENCODER
A encoder is a digital circuit that converts binary information from the 2n input to n
outputs.
Circuit N output…2N Inputs
Block Diagram of Encoder
4 X 2 ENCODER
Encoder
D1
4 X 2 Encoder
D4
D3
D2
A
B

7. D1 D2 D3 D4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
A B
0 0
0 1
1 0
1 1
D1
D4
D3
D2
A
B
4 X 2 Encoder

8. CircuitN input … 2N Inputs
Block Diagram of Decoder
2 X 4 DECODER
Decoder
D1
2 X 4 Decoder
D4
D3
D2
A
B
DECODER
A decoder is a digital circuit that converts binary information from the n coded input
to maximum of 2n outputs.

9. 2 X 4 Decoder
A
B D1
D4
D3
D2
A B D1 D2 D3 D4
0 0 1 0 0 0
0 1 0 1 0 0
1 0 0 0 1 0
1 1 0 0 0 1

10. MULTIPLEXER(MUX)
A multiplexer is a digital circuit that receives binary information from one of 2n input
data lines and directs it to a single output line.
4-to-1-line Multiplexer
S0
S1
I0
Y
S0 S1 Y
0 0 I0
0 1 I1
1 0 I2
1 1 I3
I1 I2 I3

11. DEMULTIPLEXER(DEMUX)
A demultiplexer is a digital circuit which performs the opposite operation to the MUX.
It functions as an electronic switch to route an incoming data signal to one of the
several outputs.
1-to-4-line Demultiplexer
S0
S1
Y0
D
Y1
Y2
Y3
D S0 S1 Y0 Y1 Y2 Y3
D 0 0 D 0 0 0
D 0 1 0 D 0 0
D 1 0 0 0 D 0
D 1 1 0 0 0 D

12. SEVEN SEGMENT DIGITAL CIRCUIT PROJECT
b
a
d
ce
g
f

13. b
a
d
ce
g
f
0010 a,b,d,e,g
b
a
ce
g
f
I1
I2
I3
I4

14. Digit Segments
0 abcdef
1 bc
2 abdeg
3 abcdg
4 bcfg
5 acdfg
6 acdefg
7 abc
8 abcdefg
9 abcdfg
b
a
d
ce
g
f

15. Inputs Hex Value Segments
I1 I2 I3 I4 a b c d e f g
0 0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 1 0 1 1 0 0 0 0
0 0 1 0 2 1 1 0 1 1 0 1
0 0 1 1 3 1 1 1 1 0 0 1
0 1 0 0 4 0 1 1 0 0 1 1
0 1 0 1 5 1 0 1 1 0 1 1
0 1 1 0 6 1 0 1 1 1 1 1
0 1 1 1 7 1 1 1 0 0 0 0
1 0 0 0 8 1 1 1 1 1 1 1
1 0 0 1 9 1 1 1 1 0 1 1
b
a
d
ce
g
f

16. Clock
In many digital circuits the order in which events happen is critical. Sometimes one
event must precede another, sometimes two events must occur simultaneously. To
allow designers to achieve the required timing relations, many digital circuits use
clocks to provide synchronization.
A clock in this context is a circuit that emits a series of pulses with a precise pulse
width and precise interval between consecutive pulses.
The interval between corresponding edges of two consecutive pulses is called the
clock cycle time.
To achieve high accuracy, the clock frequency is usually controlled by a crystal
oscillator.
Delay
C1
C2
Clock cycle
Crystal Oscillator

17. Flip Flop
To store 1-bit value we need a circuit that somehow “remembers” previous input
values. This circuit is called flip-flop. There are variety of flip flops, all of which share
two properties.
• The flip flop is a bi-stable device. It exist in one of two states. In the absence of
input remains in that state. Thus a flip flop can function as a 1-bit memory.
• The flip flop has two outputs, which are always the complements of each other.
These are generally labeled Q and Q’.
•In electronics, a flip-flop or latch is a circuit that has two stable states and can be
used to store state information. Flip Flop is a bistable multivibrator. The circuit can be
made to change state by signals applied to one or more control inputs and will have
one or two outputs. It is the basic storage element in sequential logic. Flip-flops and
latches are a fundamental building block of digital electronics systems used in
computers, communications, and many other types of systems.
•Flip-flops and latches are used as data storage elements. Such data storage can be
used for storage of state, and such a circuit is described as sequential logic. When
used in a finite-state machine, the output and next state depend not only on its
current input, but also on its current state (and hence, previous inputs). It can also be
used for counting of pulses, and for synchronizing variably-timed input signals to
some reference timing signal.
•Flip-flops can be either simple (transparent or opaque) or clocked (synchronous or edge-
triggered); the simple ones are commonly called latches.The word latch is mainly used for

18. SR Flip Flop [ SET RESET FLIP FLOP ]
S
R
Q
Q’
0
0
1
0
1
0
The above circuit is known as SR Flip Flop.
It has two inputs, S for Setting the flip flop and R for Resetting (Clearing) flip flop.
It also has two outputs, Q and Q’ which are complementary.
If S=0 R=0 and Q=0 then First NOR gate output is 1(Q’) and Second NOR gate output is 0.
If S=0 R=0 and Q=1 then First NOR gate output is 0(Q’) and Second NOR gate output is 1.
If S=1 R=0 and Q=0 then First NOR gate output is 0(Q’) and Second NOR gate output is 1(Q). (Set Operation)
If S=0 R=1 and Q=1 then Second NOR gate output is 0(Q) and first NOR gate output is 1(Q’). (Reset Operation)
S R Q Q’
0 0 Q Q’
1 0 1 0
0 1 0 1
1 1 - -

19. Clocked SR Flip Flop [ SET RESET FLIP FLOP ]
S
R
Q
Q’
0
0
1
0
1
0
S R Clock Q Q’
0 0 0 Q Q’
0 0 1 Q Q’
1 0 0 Q Q’
1 0 1 1 0
0 1 0 Q Q’
0 1 1 0 1
1 1 0 Q Q’
1 1 1 - -
S
R
Q’
Q
Ck

20. Clocked D Flip Flop [ DATA FLIP FLOP ]
D
Q
Q’
1
0
1
0
D Clock Q Q’
0 0 Q Q’
0 1 0 1
1 0 Q Q’
1 1 1 0
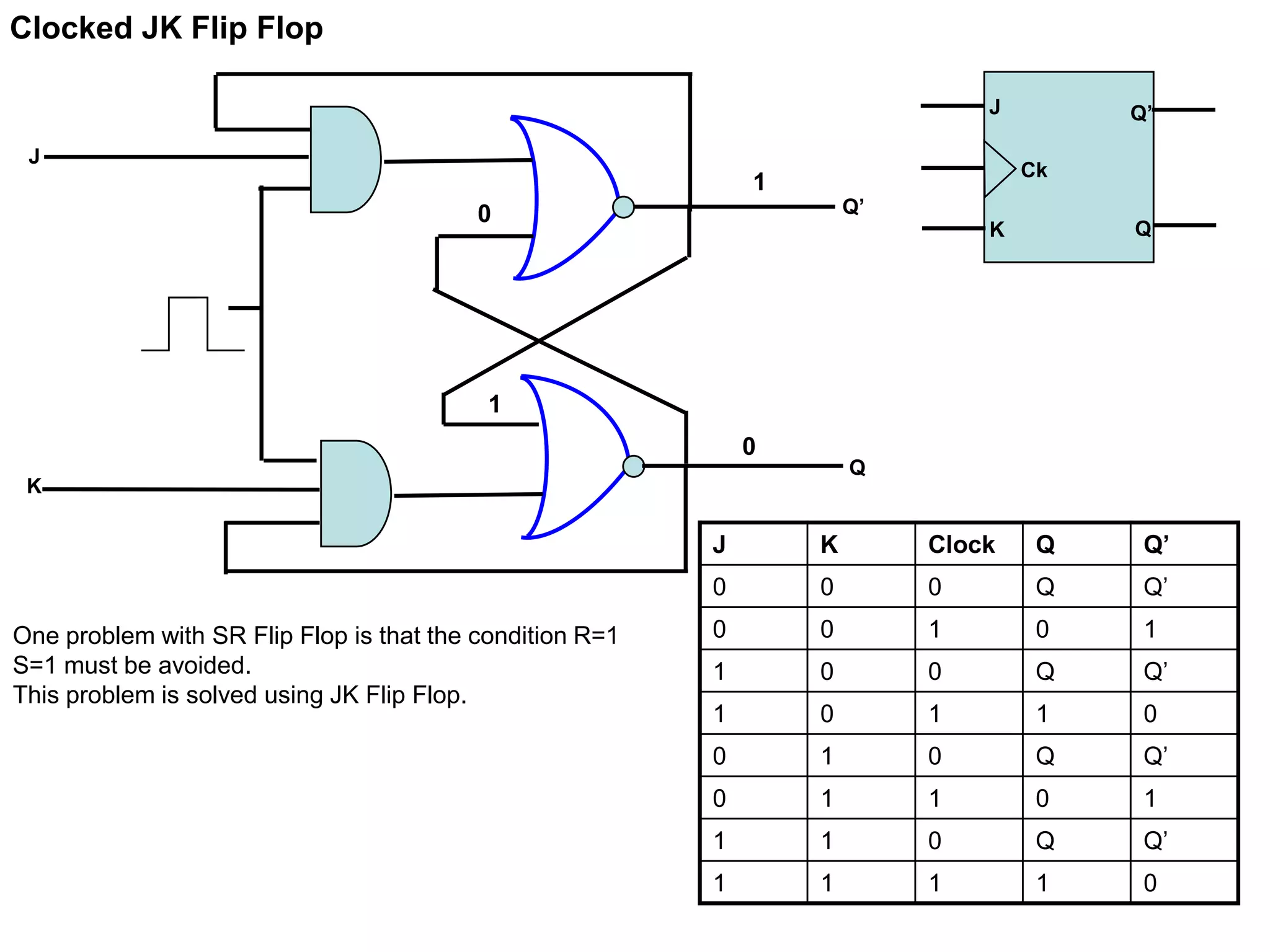
One problem with SR Flip Flop is that the condition R=1 S=1 must be avoided.
One way to do this is to allow just a single input.
The D Flip Flop accomplish this.
In D Flip Flop one input D is split into two inputs. One input is inverted using Inverter. Both inputs are given
two AND gates.
The D Flip Flop is also known as Data Flip Flop because it is used to store 1-bit data.
D Q’
Q
Ck

21. Clocked JK Flip Flop
J
Q
Q’
1
0
1
0
K
J K Clock Q Q’
0 0 0 Q Q’
0 0 1 0 1
1 0 0 Q Q’
1 0 1 1 0
0 1 0 Q Q’
0 1 1 0 1
1 1 0 Q Q’
1 1 1 1 0
One problem with SR Flip Flop is that the condition R=1
S=1 must be avoided.
This problem is solved using JK Flip Flop.
J
K
Q’
Q
Ck

22. D Flip-Flop from NAND Latch
•The output Q will track the input D so long as the flip-flop remains enabled.
•A D flip-flop constructed from a NAND-latch .
Clocked D Flip Flop

23. Clocked J K Flip Flop using NAND Gates:
The J-K flip-flop is the most versatile of the basic flip-flops. It has the input- following
character of the clocked D flip-flop but has two inputs,traditionally labeled J and K. If J
and K are different then the output Q takes the value of J at the next clock edge.
A simplified version of the versatile J-K flip-flop. Note that the outputs feed back to the
enabling NAND gates. This is what gives the toggling action when J=K=1.

24. Definitions
Combinational Circuit
A combinational circuit is a connected arrangement of logic gates with set of inputs and outputs. At any given time, the binary
values of the outputs are function of the binary combination of the inputs.
N inputs M outputs
Examples : Encoder, Decoder, Adder, Multiplexer, Demultiplexer
Sequential Circuit
A sequential circuit is an interconnection of flip flops and gates. The gates by themselves constitute a combinational circuit, but
when included with the flip flops, the overall circuit is classified as a sequential circuit.
Combinational Circuit
Flip Flops
Clock
Inputs Outputs
Examples : SR Flip Flop, D Flip Flop, JK Flip Flop

25. Integrated Circuit (IC/ IC Chip)
Developed in the 1950s by Jack Kilby of Texas Instruments and Robert Noyce of Fairchild Semiconductor.
Gates are not manufactured or sold individually but rather in units called Integrated Circuits, often called ICs or
chips.
•An IC is a square piece of silicon about 5 X 5 mm on which some gates have been deposited.
•An integrated circuit or monolithic integrated circuit (also referred to as an IC, a chip, or a microchip) is a set of
electronic circuits on one small plate ("chip") of semiconductor material, normally silicon. This can be made
much smaller than a discrete circuit made from independent components.
•Integrated circuits are used in virtually all electronic equipment today and have revolutionized the world of
electronics. Computers, mobile phones, and other digital home appliances are now inextricable parts of the
structure of modern societies, made possible by the low cost of producing integrated circuits.
•ICs can be made very compact, having up to several billion transistors and other electronic components in an
area the size of a fingernail. The width of each conducting line in a circuit (the line width) can be made smaller
and smaller as the technology advances, in 2008 it dropped below 100 nanometers and in 2013 it is expected
to be in the teens of nanometers
Chips can be divided into classes based on the number of gates they contain :
•SSI Circuit (Small Scale Integration) : 1 to 10 gates
•MSI Circuit (Medium Scale Integration) : 10 to 100 gates
•LSI Circuit (Large Scale Integration) :100 to 1,00,000 gates
VLSI Circuit (Very Large Scale Integration) : > 1,00,000 gates
•ULSI (Ultra large-scale integration): More than 1 million electronic components per chip
•WSI
•SoC
•3D IC

26. Wafer-scale integration (WSI) is a system of building very-large integrated
circuits that uses an entire silicon wafer to produce a single "super-chip".
Through a combination of large size and reduced packaging, WSI could lead to
dramatically reduced costs for some systems, notably massively parallel
supercomputers. The name is taken from the term Very-Large-Scale
Integration, the current state of the art when WSI was being developed.
A system-on-a-chip (SoC or SOC) is an integrated circuit in which all the
components needed for a computer or other system are included on a single
chip. The design of such a device can be complex and costly, and building
disparate components on a single piece of silicon may compromise the efficiency
of some elements. However, these drawbacks are offset by lower manufacturing
and assembly costs and by a greatly reduced power budget: because signals
among the components are kept on-die, much less power is required (see
Packaging).
A three-dimensional integrated circuit (3D-IC) has two or more layers of
active electronic components that are integrated both vertically and horizontally
into a single circuit. Communication between layers uses on-die signaling, so
power consumption is much lower than in equivalent separate circuits. Judicious
use of short vertical wires can substantially reduce overall wire length for faster
operation.

27. 4-bit Parallel Register
D Q’
Q
Ck
D Q’
Q
Ck
D Q’
Q
Ck
D Q’
Q
Ck
Clock
D1 D2 D3 D4
D5 D6 D7 D8
Input Lines
Output Lines
D1
D2
D3
D4

28. 4-bit Shift Register
D Q’
Q
Ck
D Q’
Q
Ck
D Q’
Q
Ck
D Q’
Q
Ck
Clock
Serial In
Serial Out
Serial in