Downloaded 44 times
Uploaded byHsien-Hsin Sean Lee, Ph.D.
Lec14 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Sequential Logic
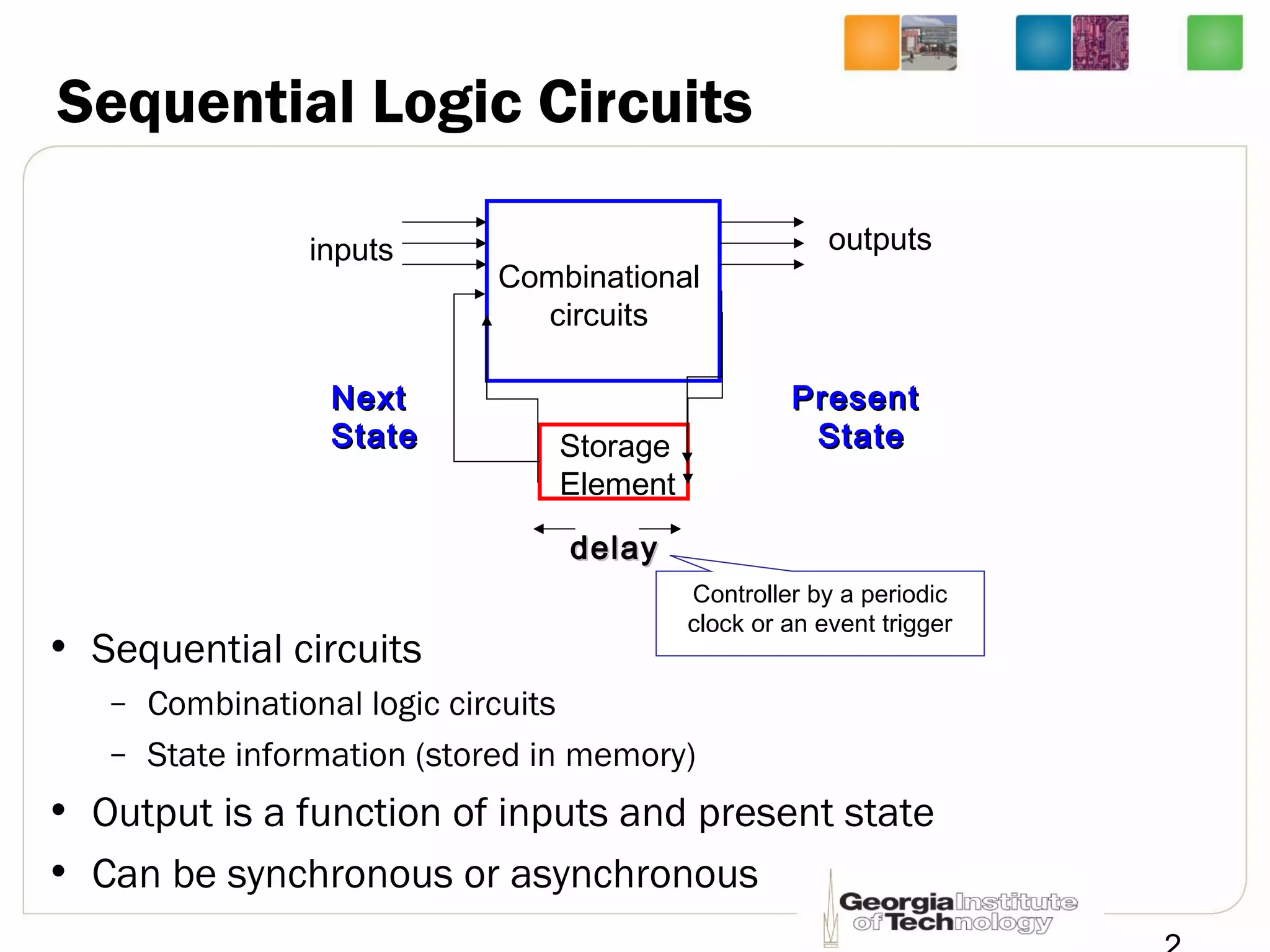
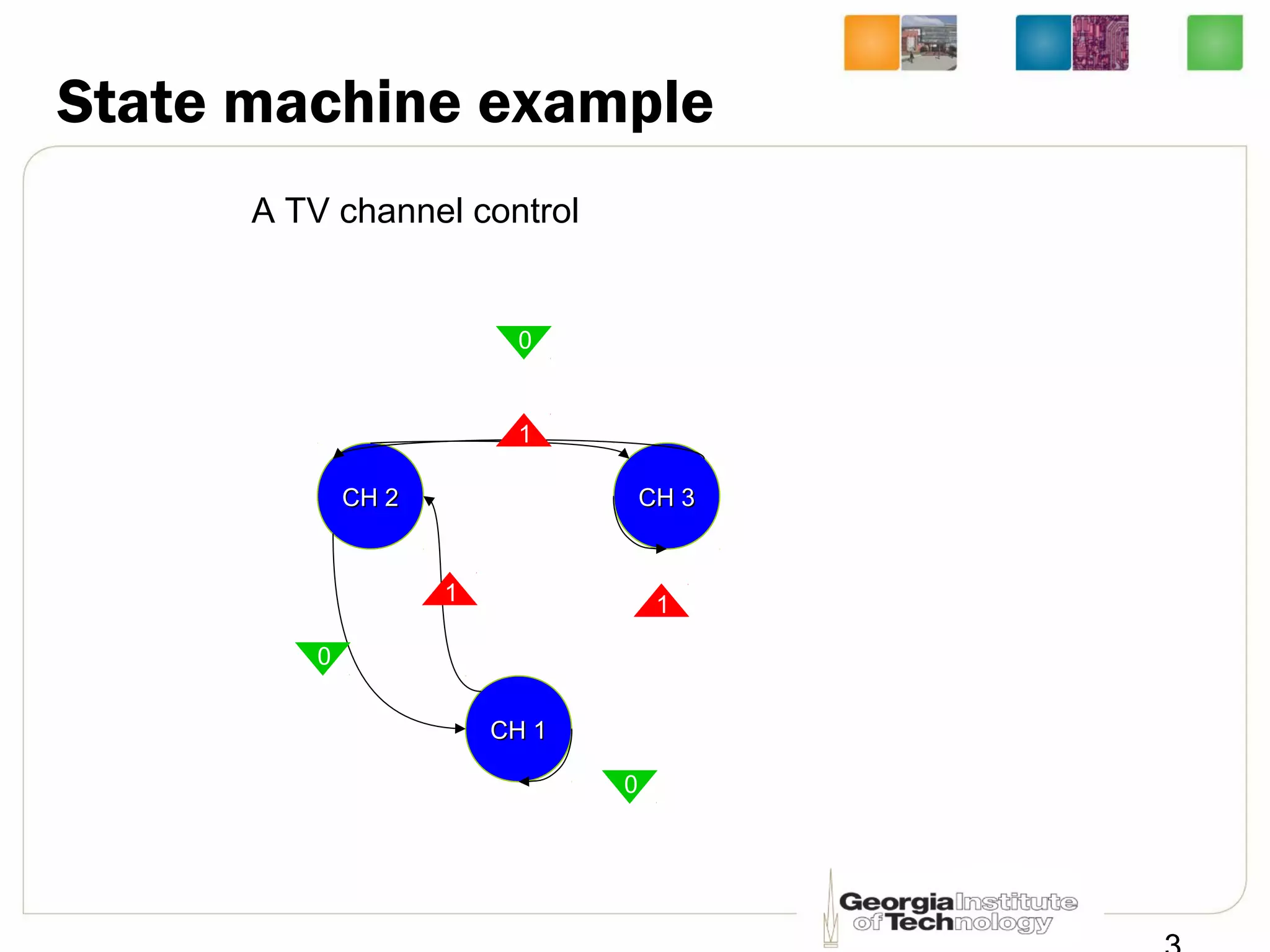
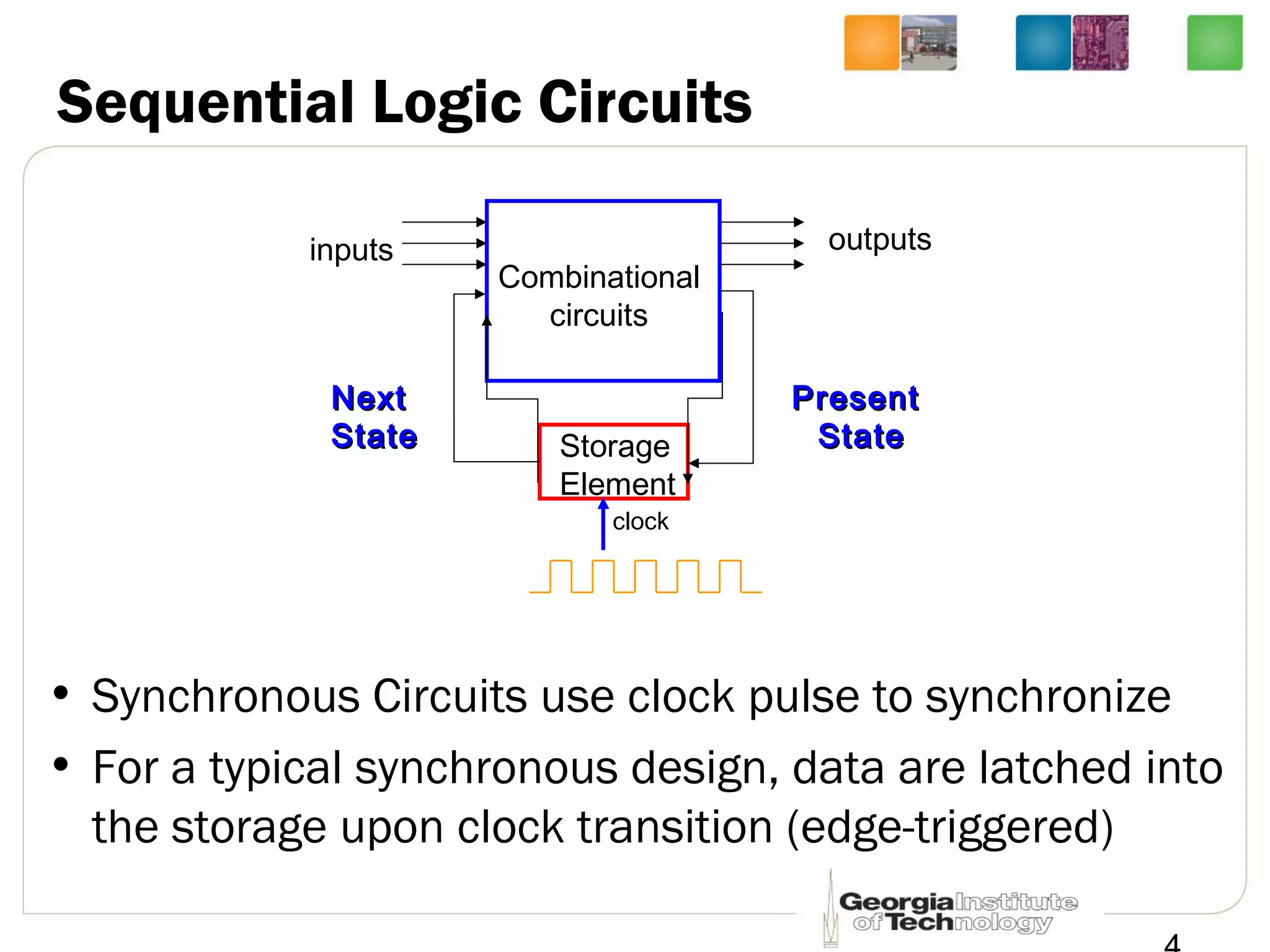
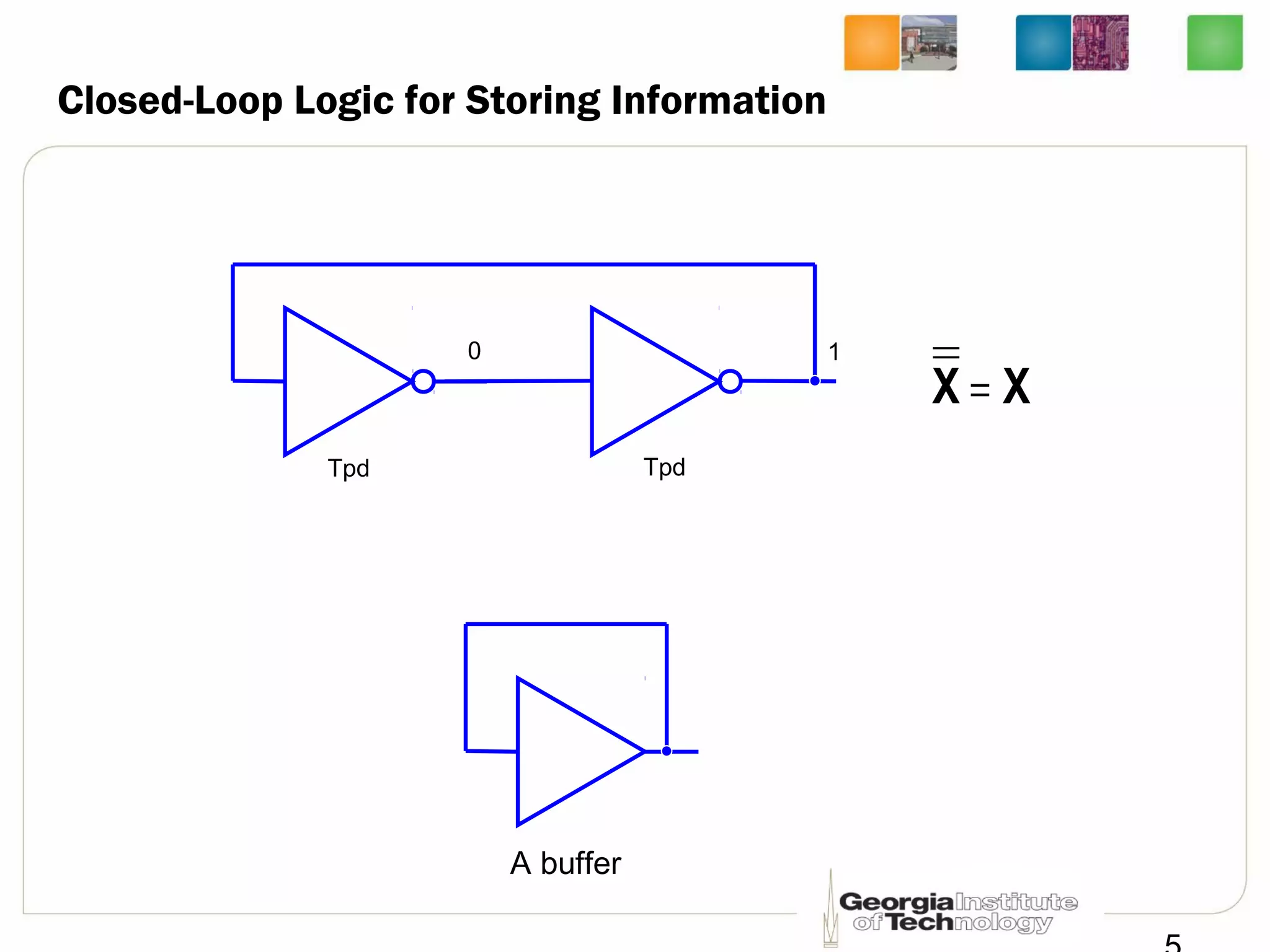
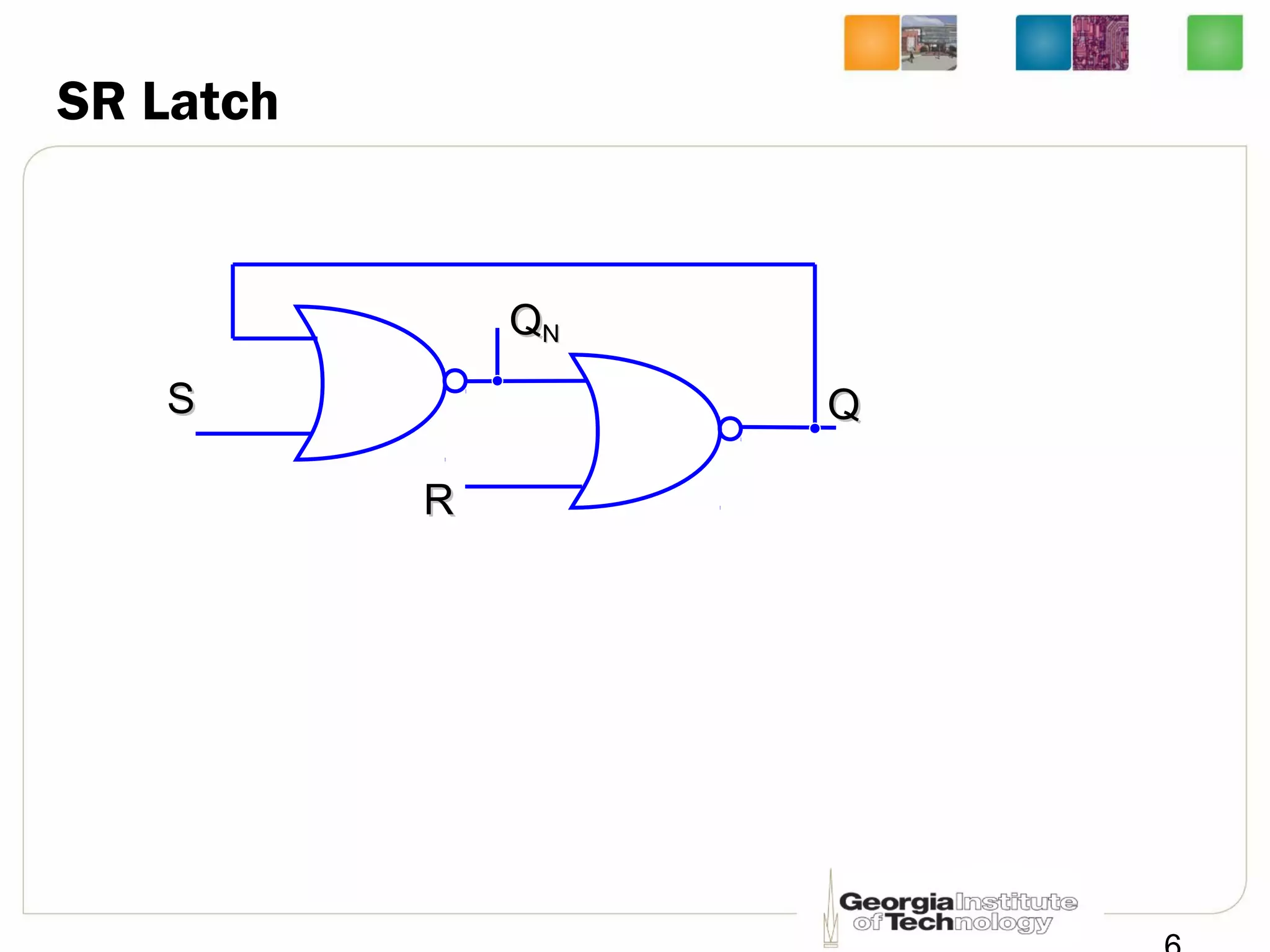
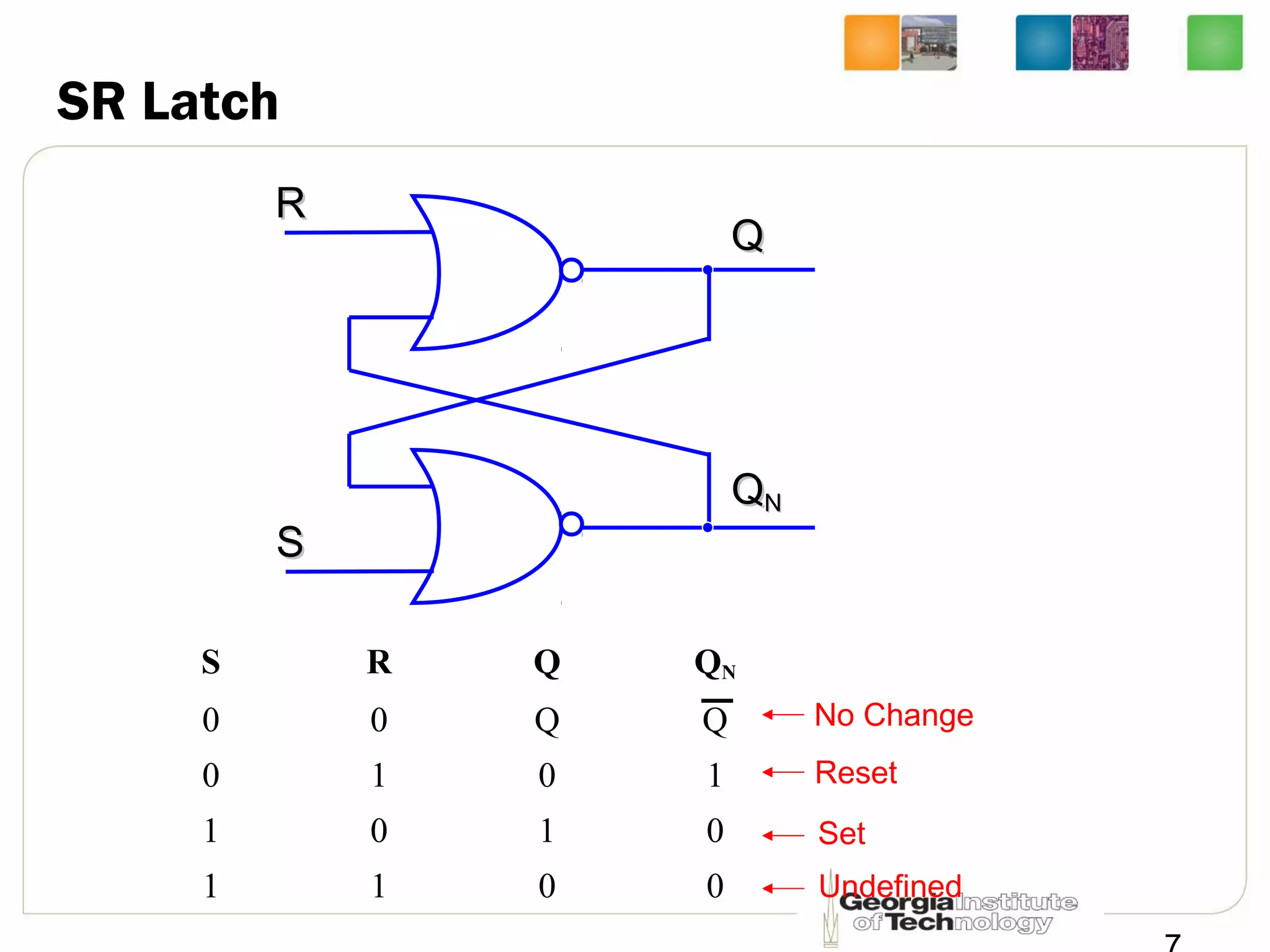
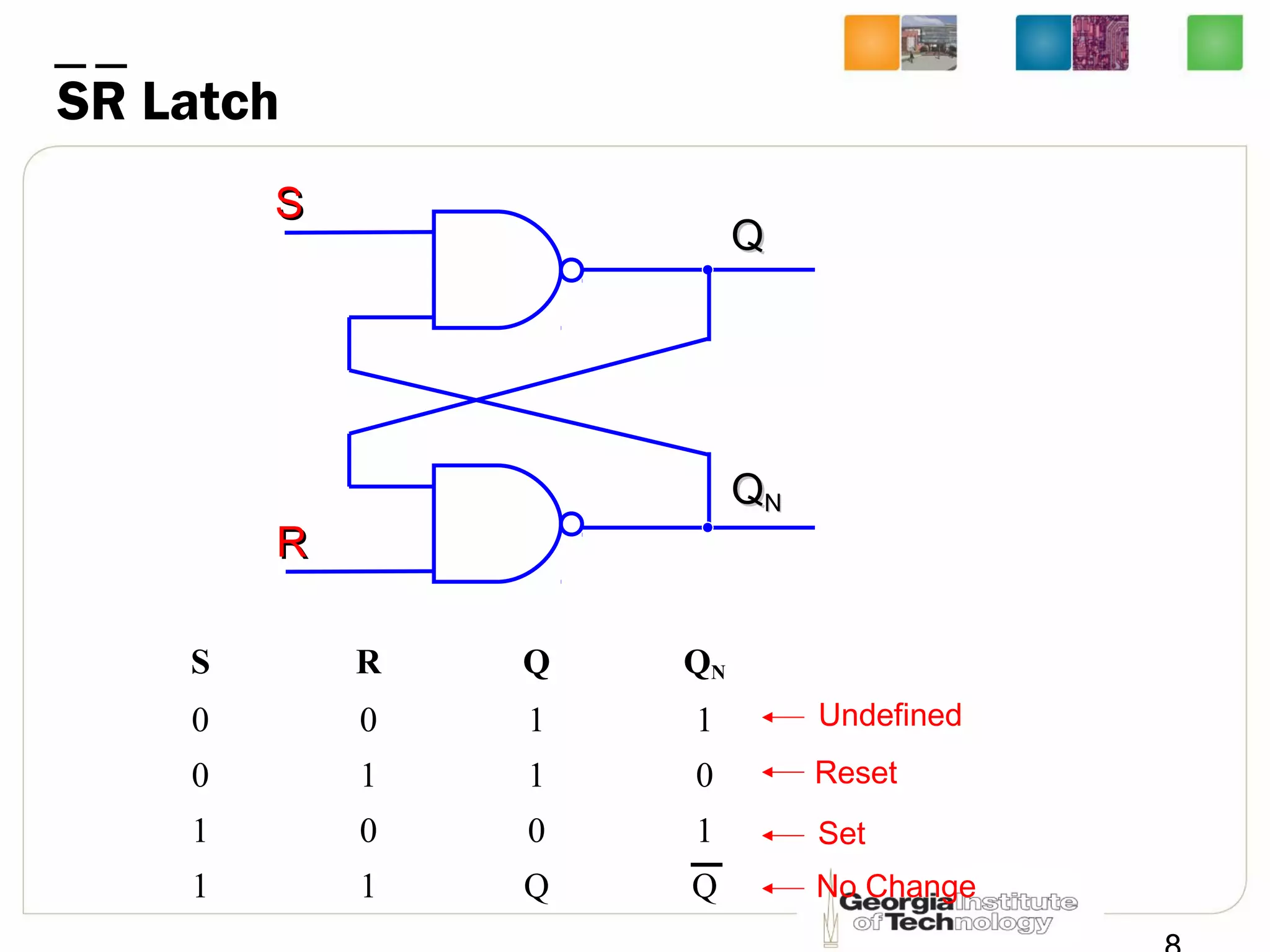
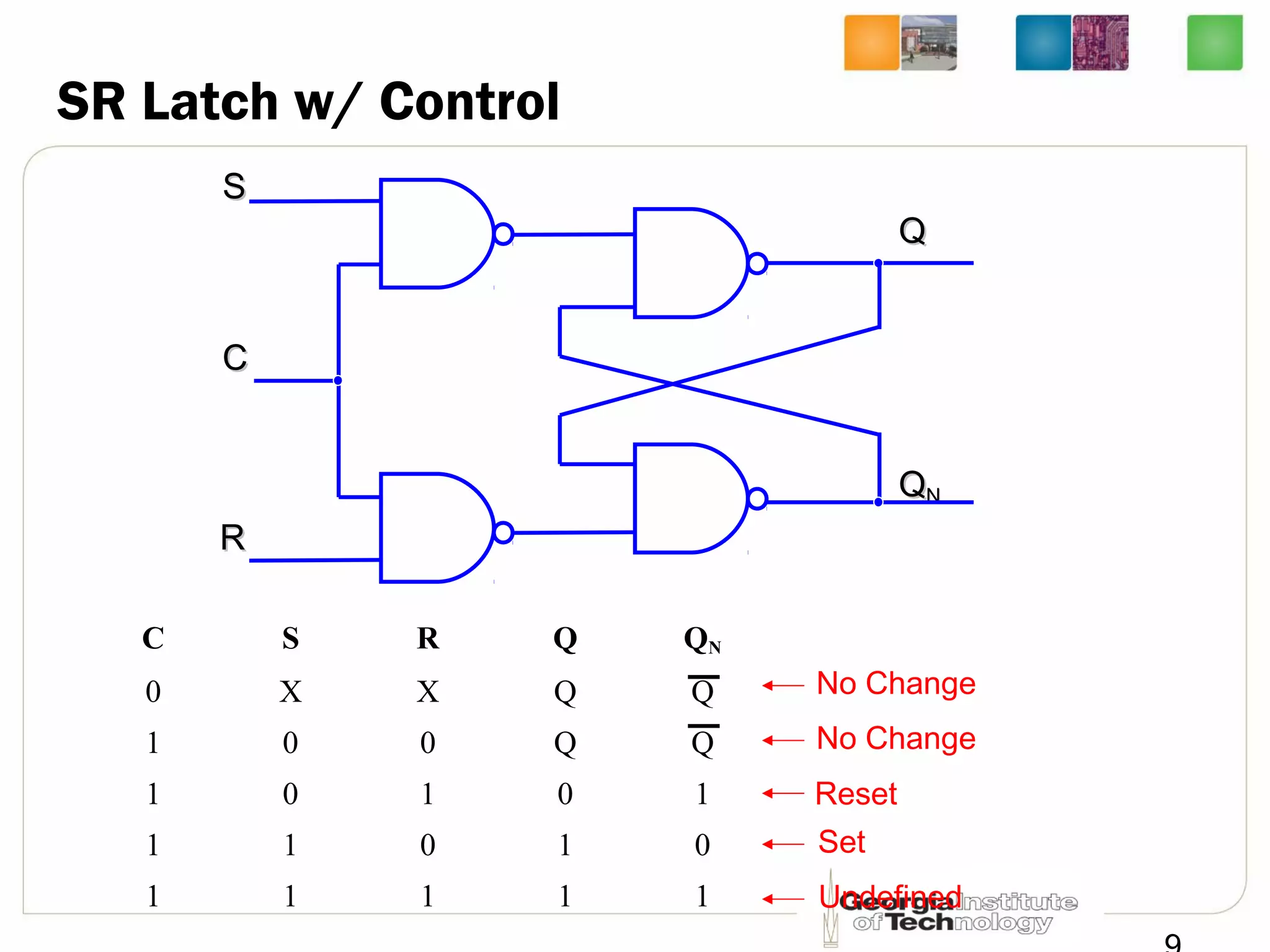
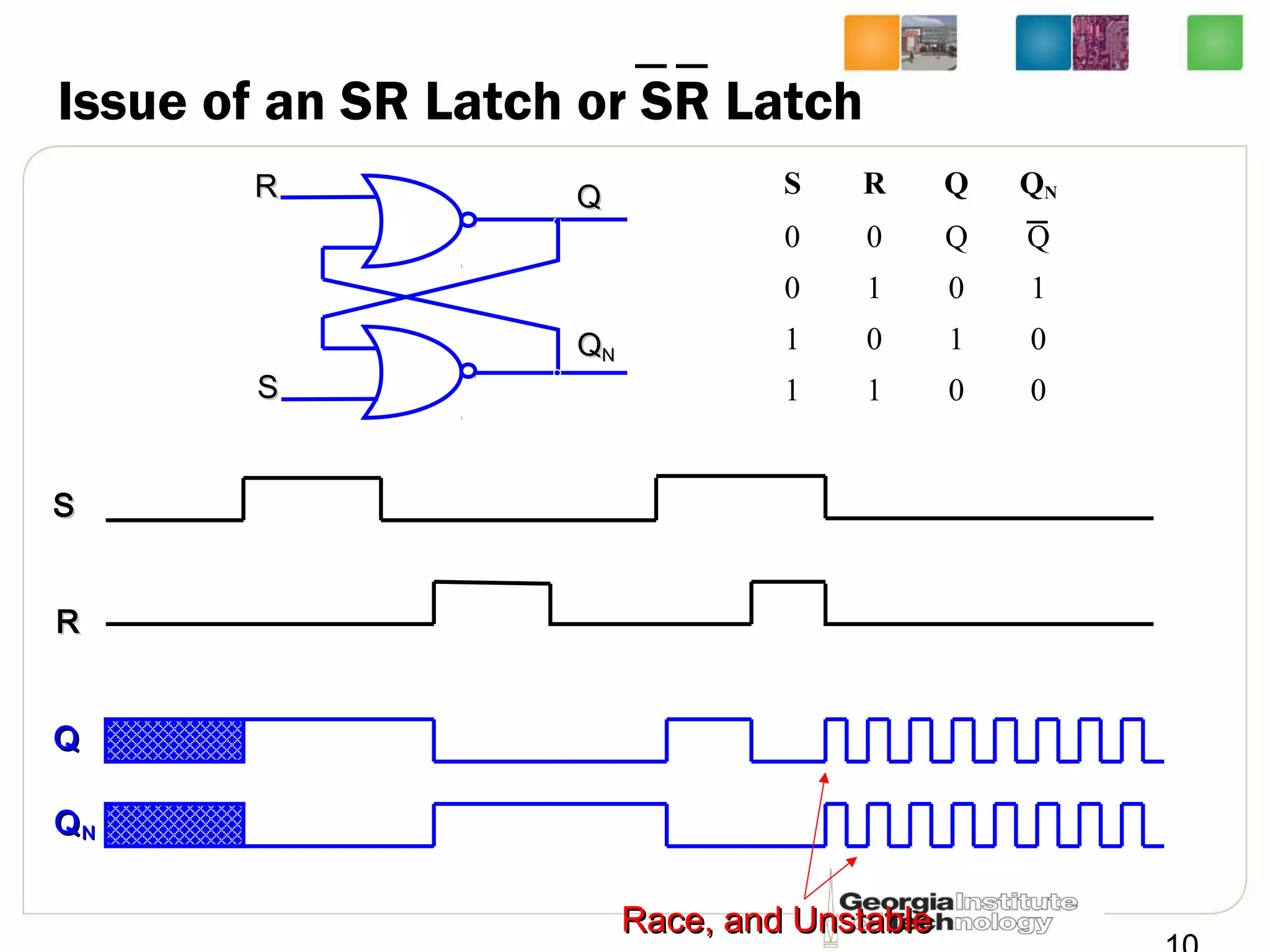
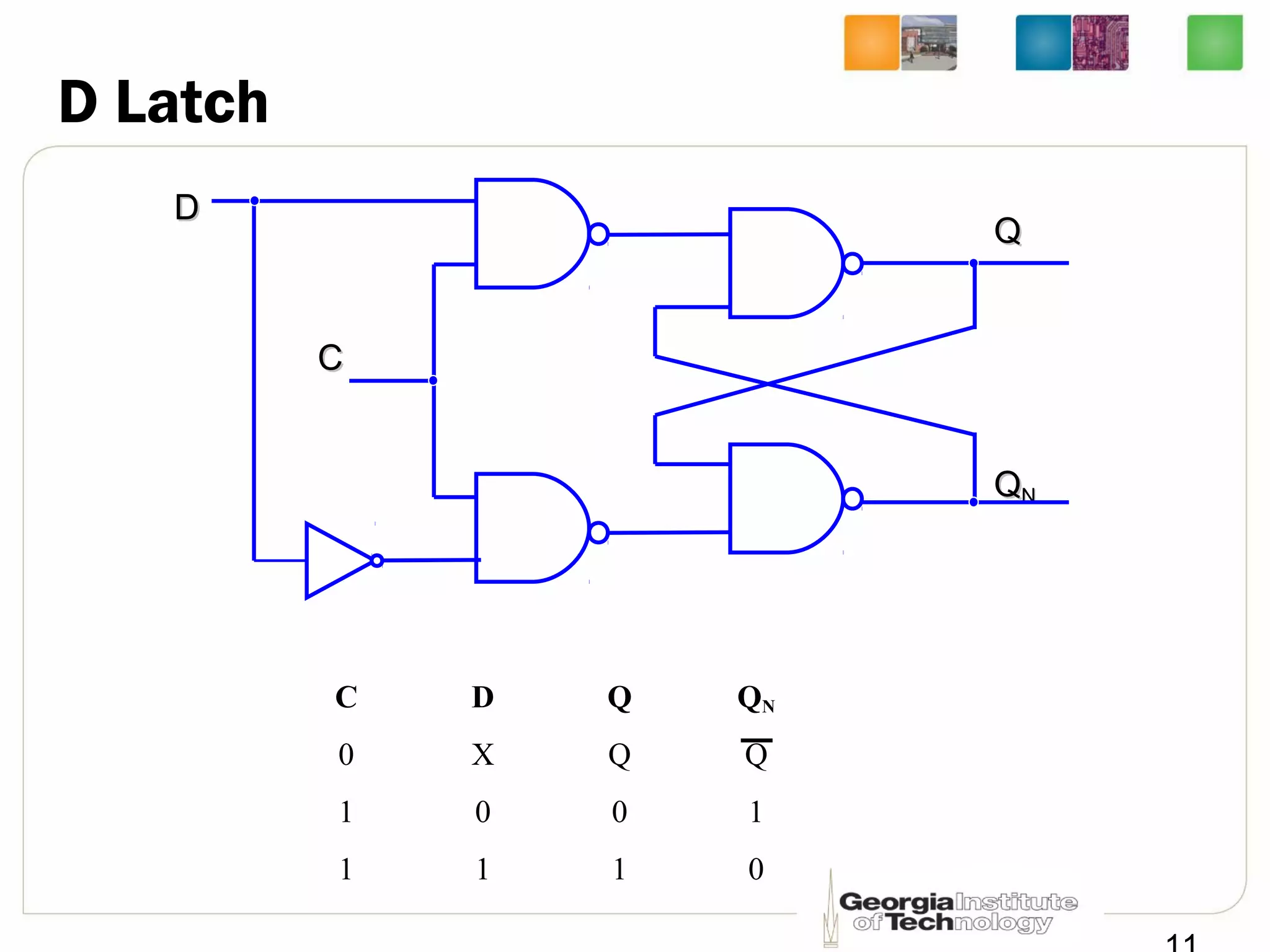
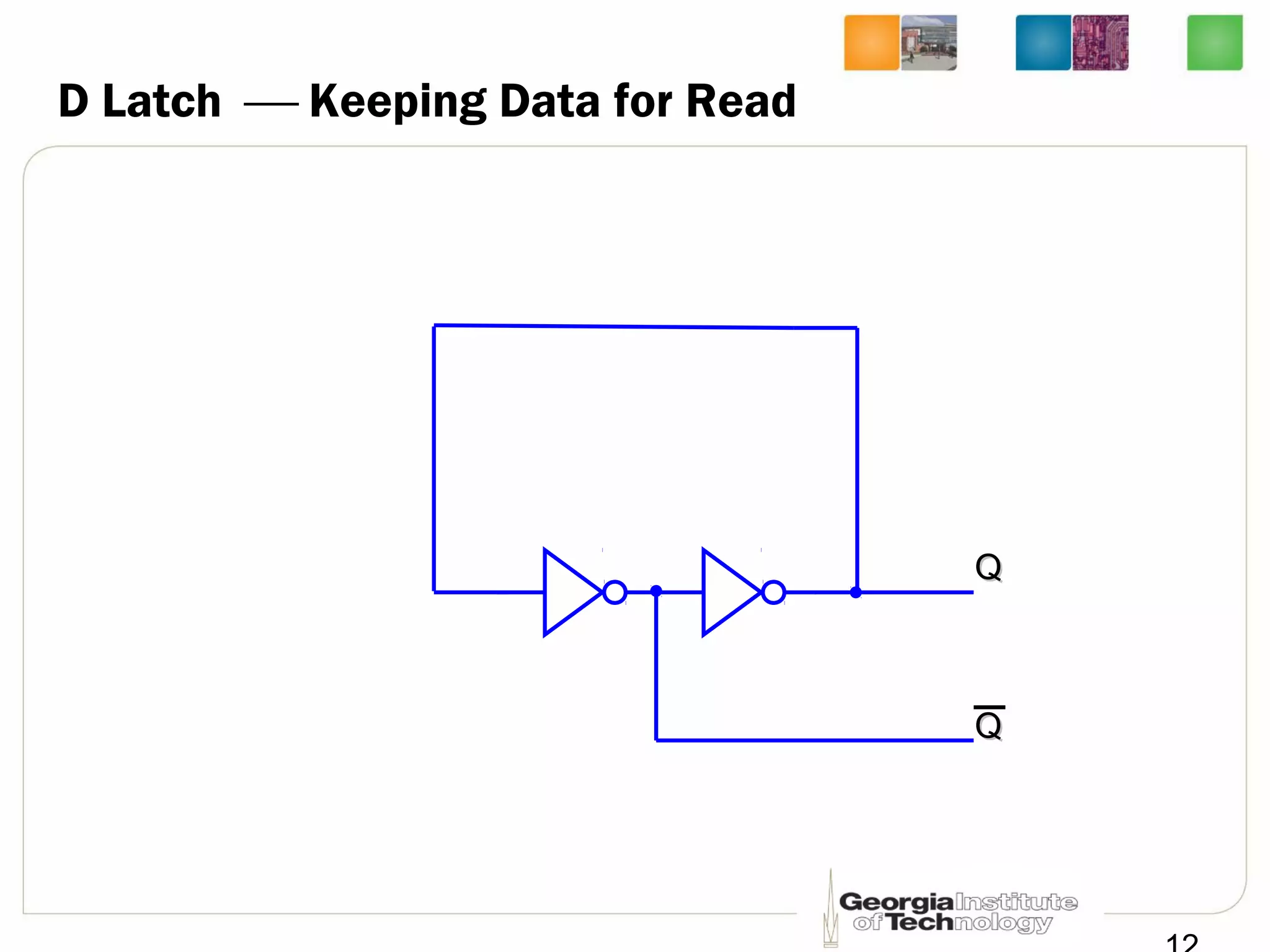
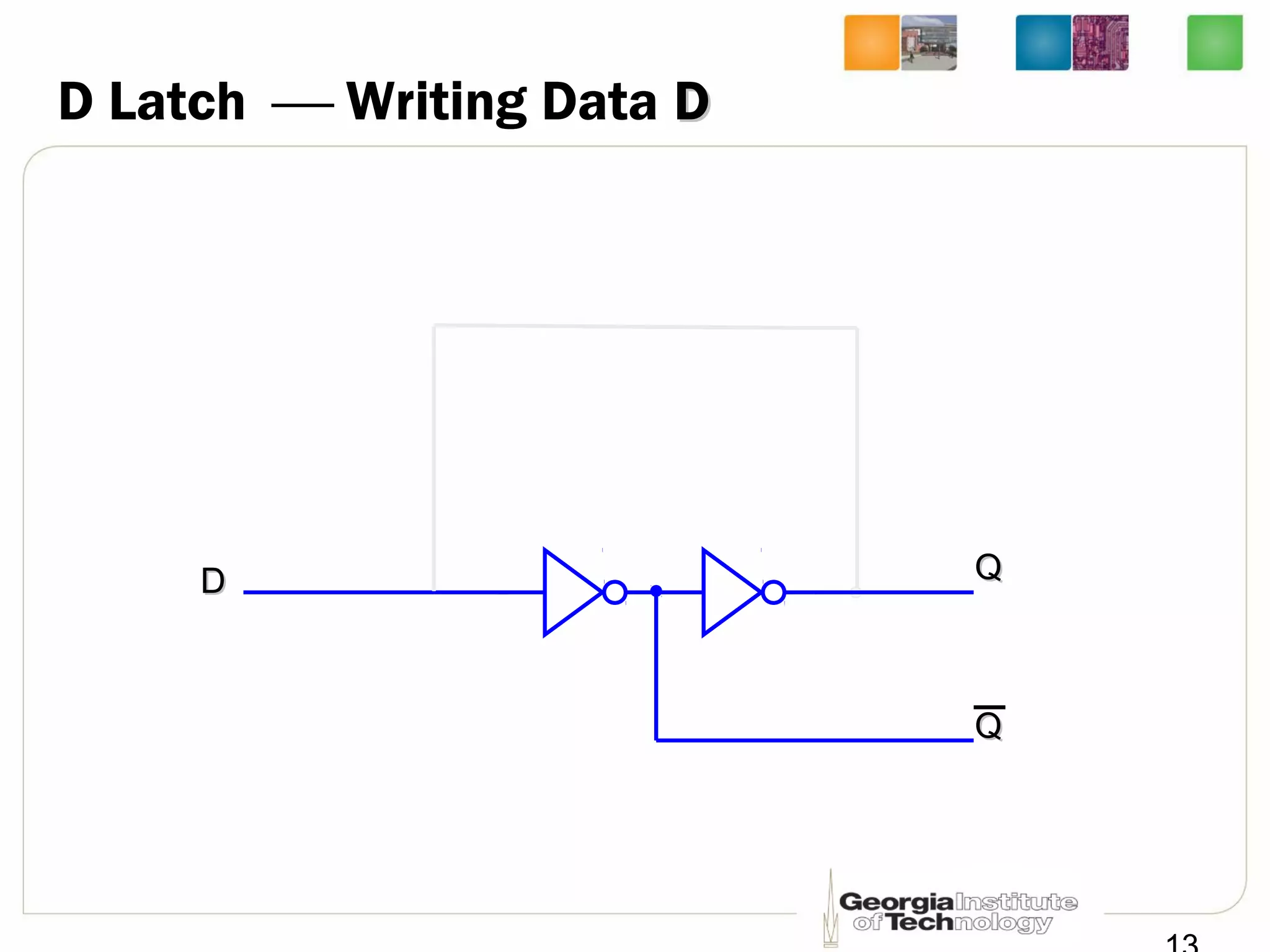
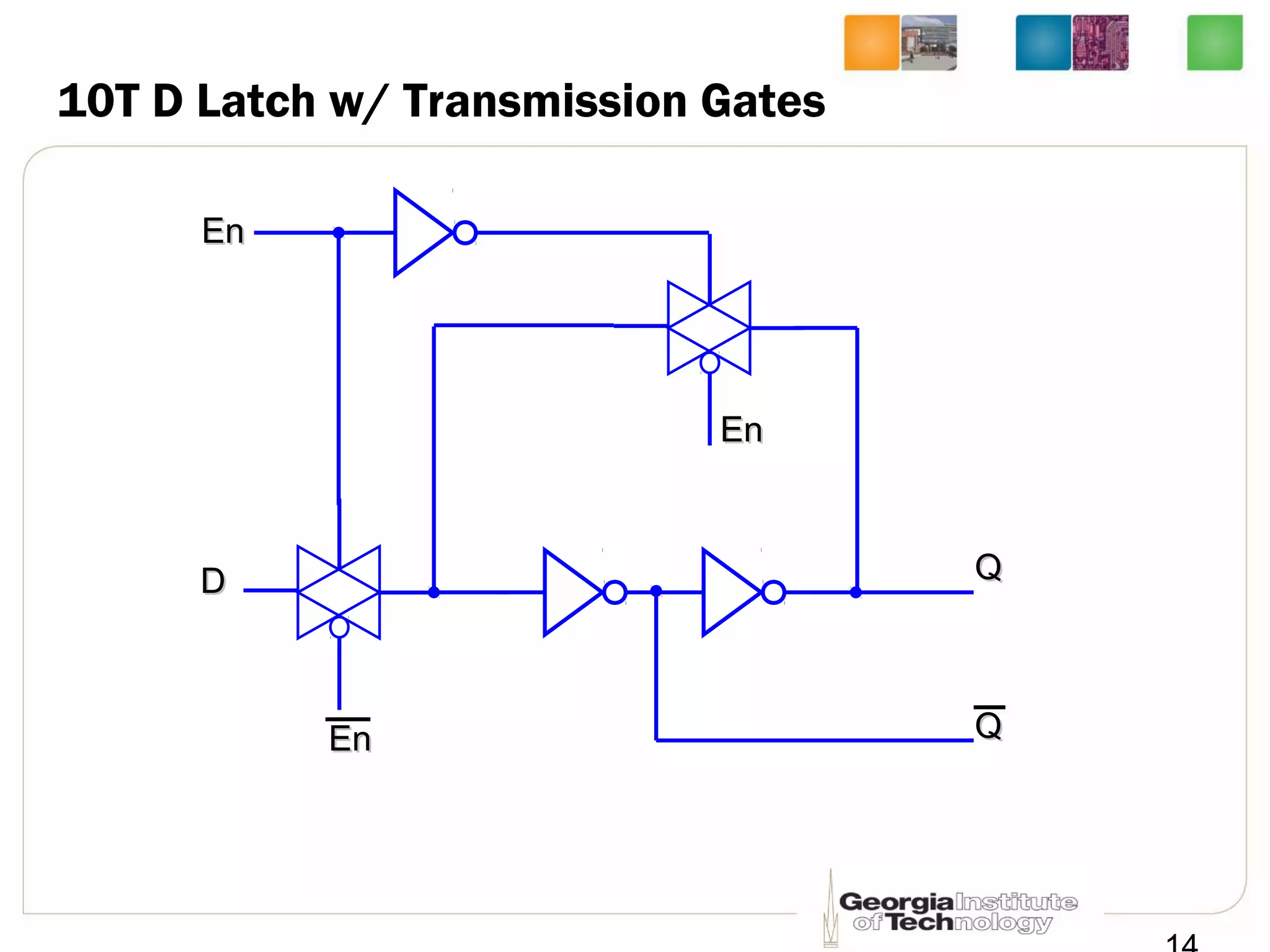
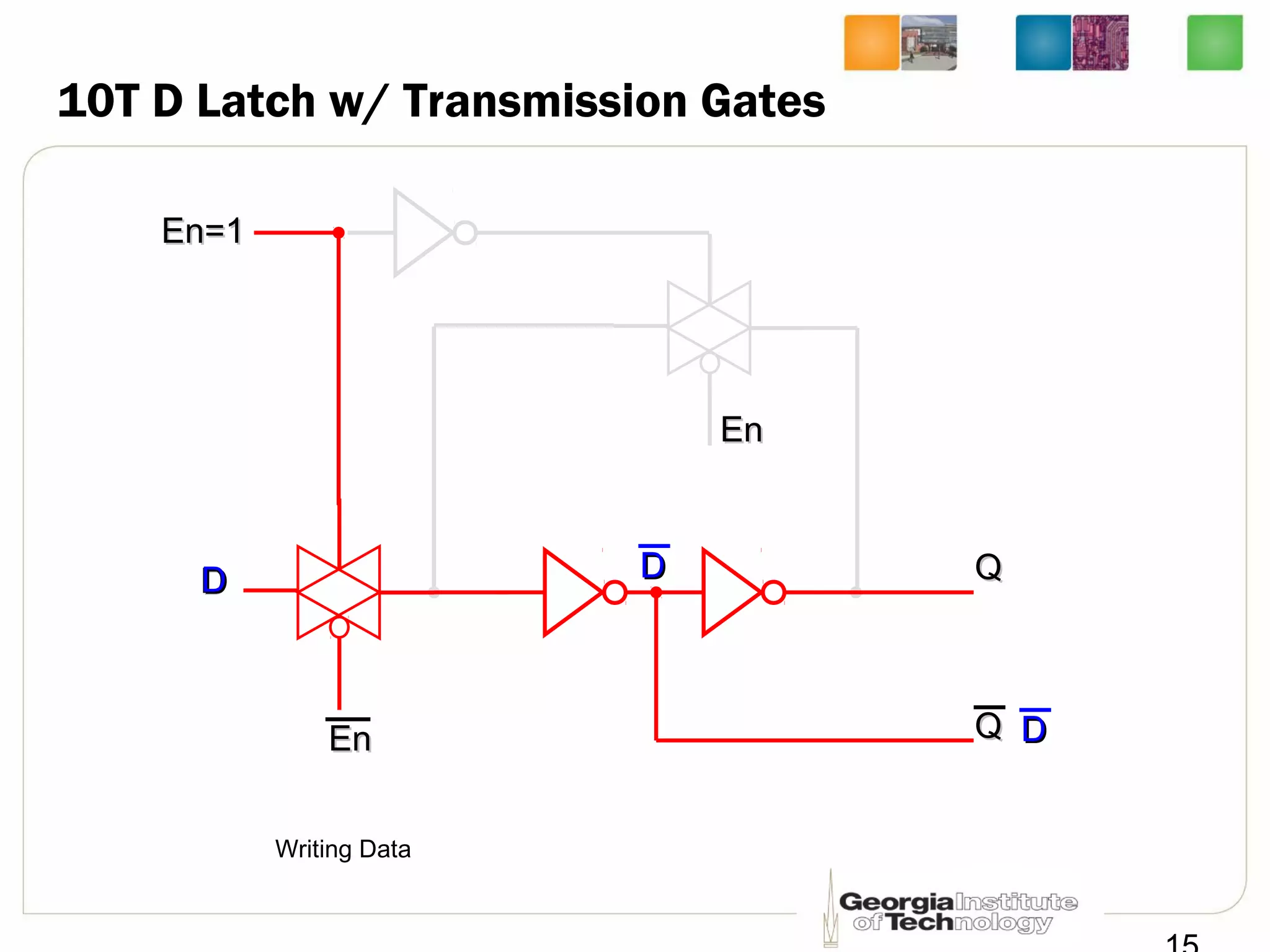
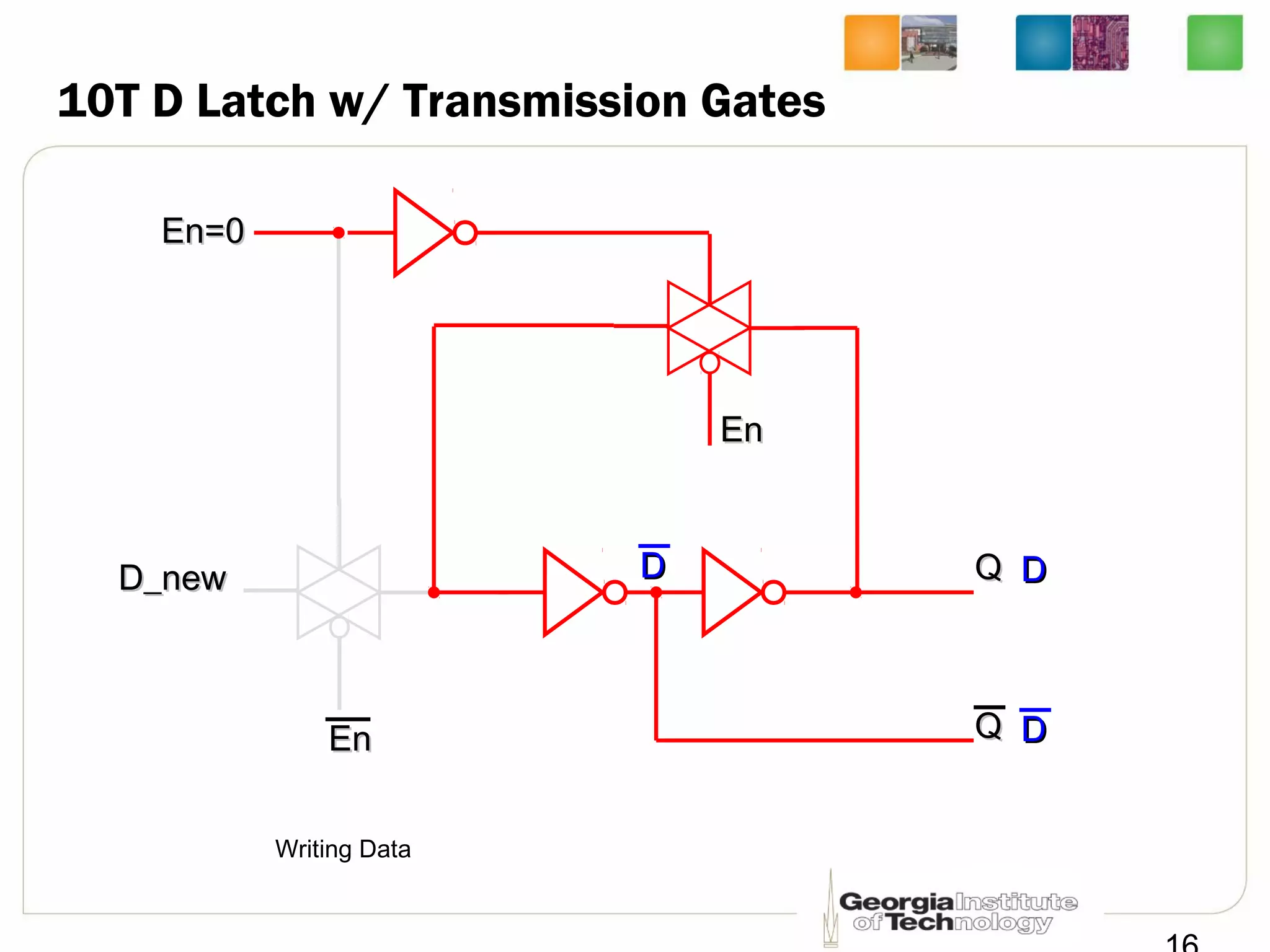
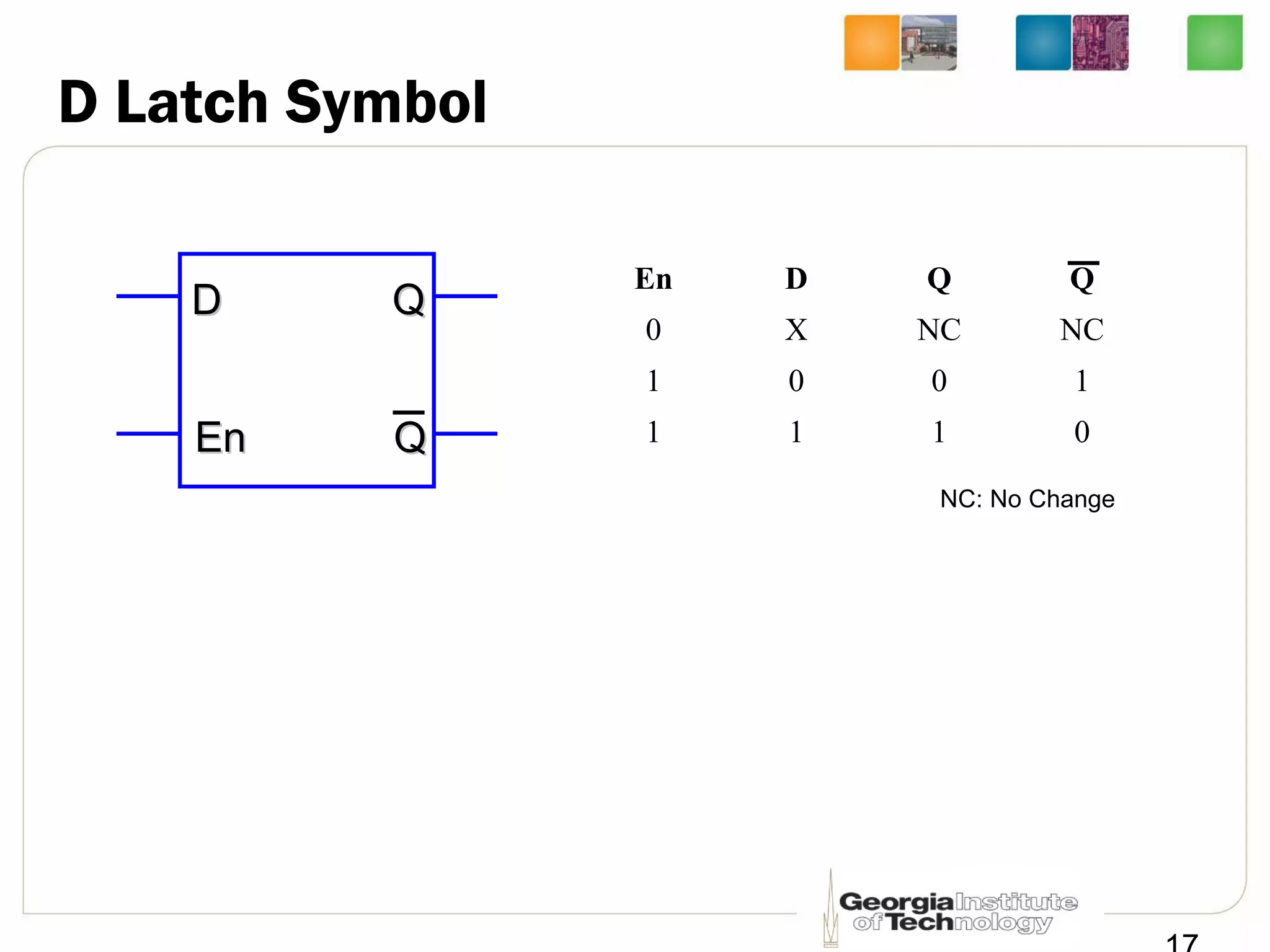
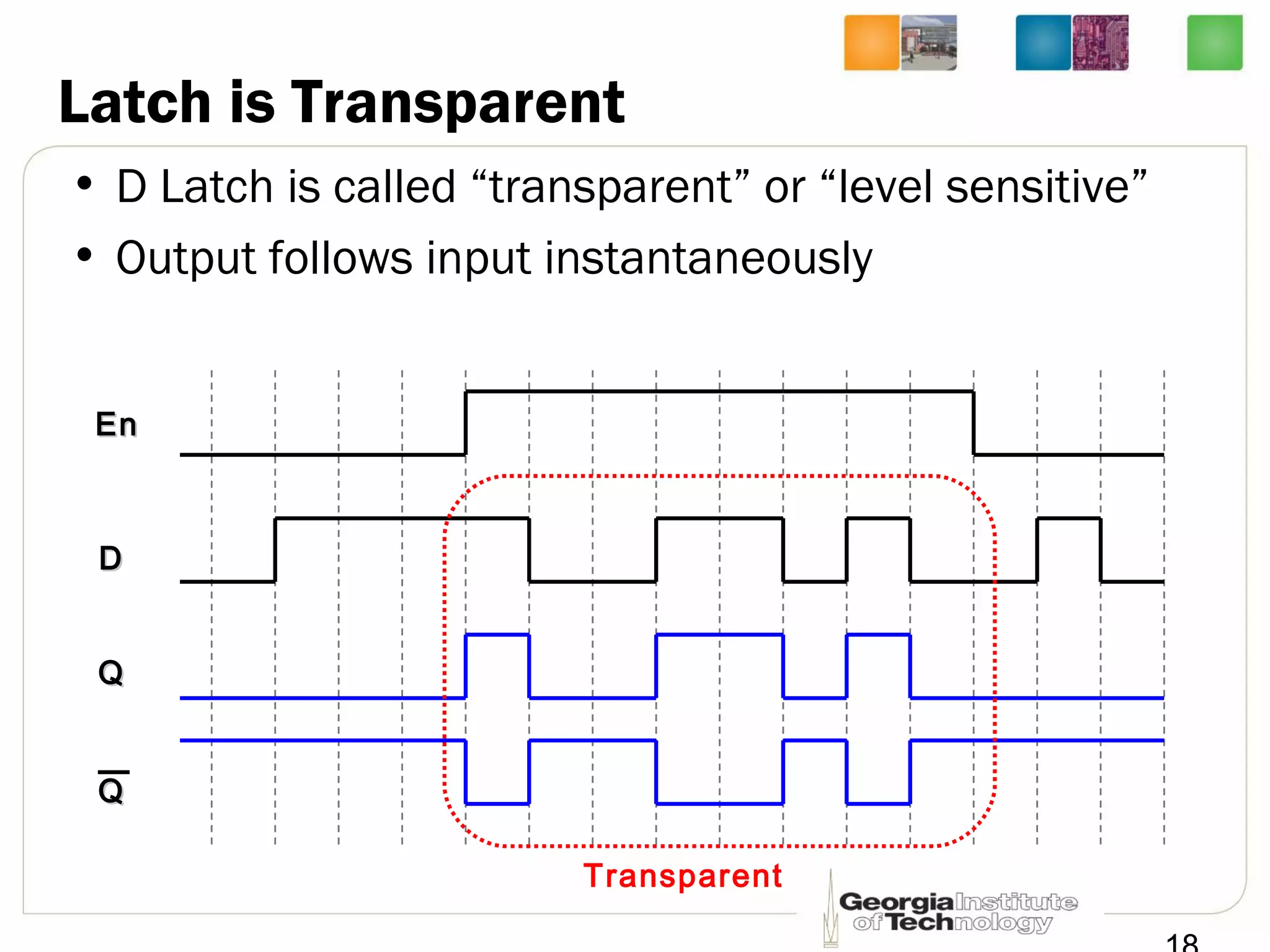
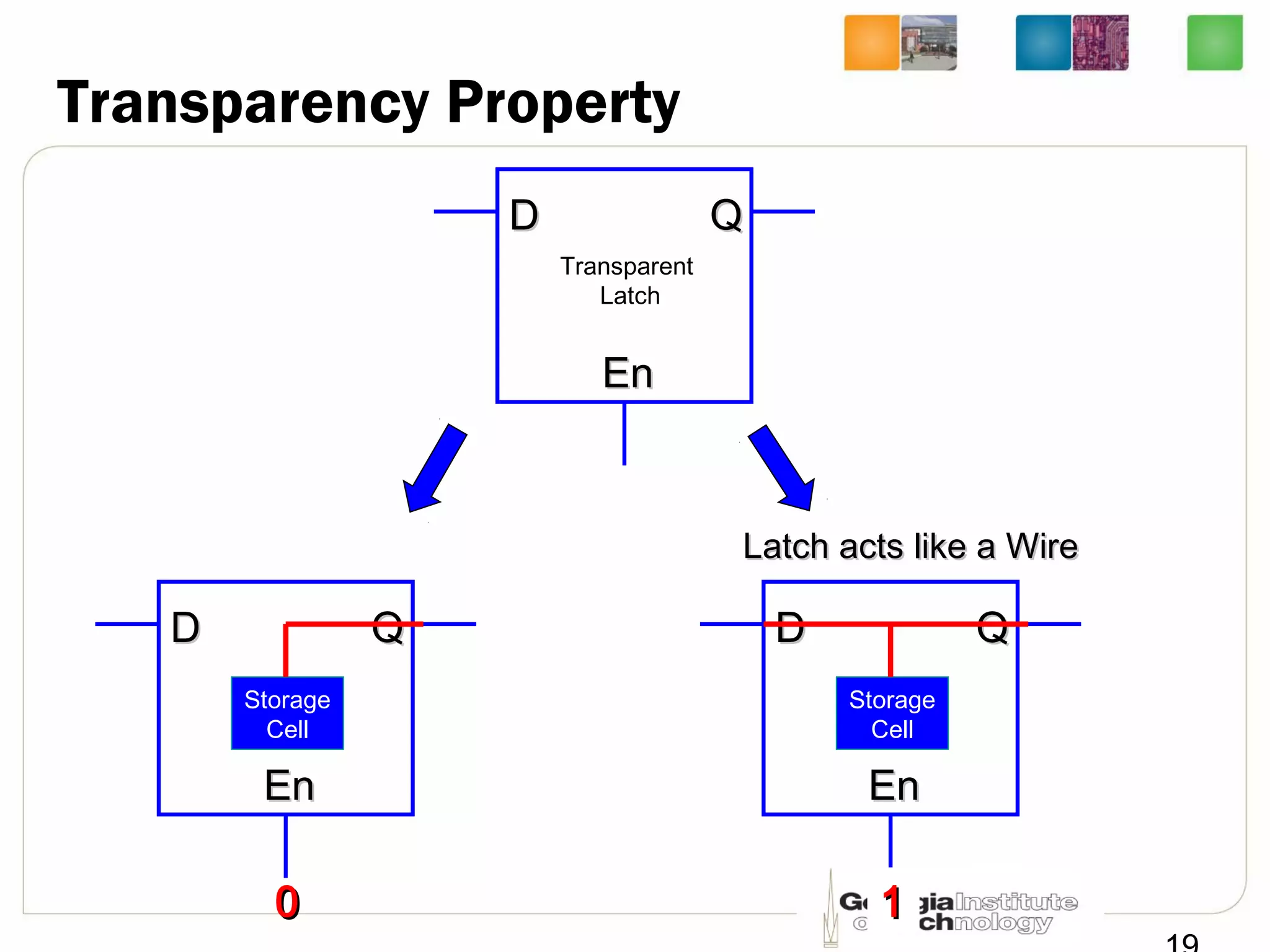
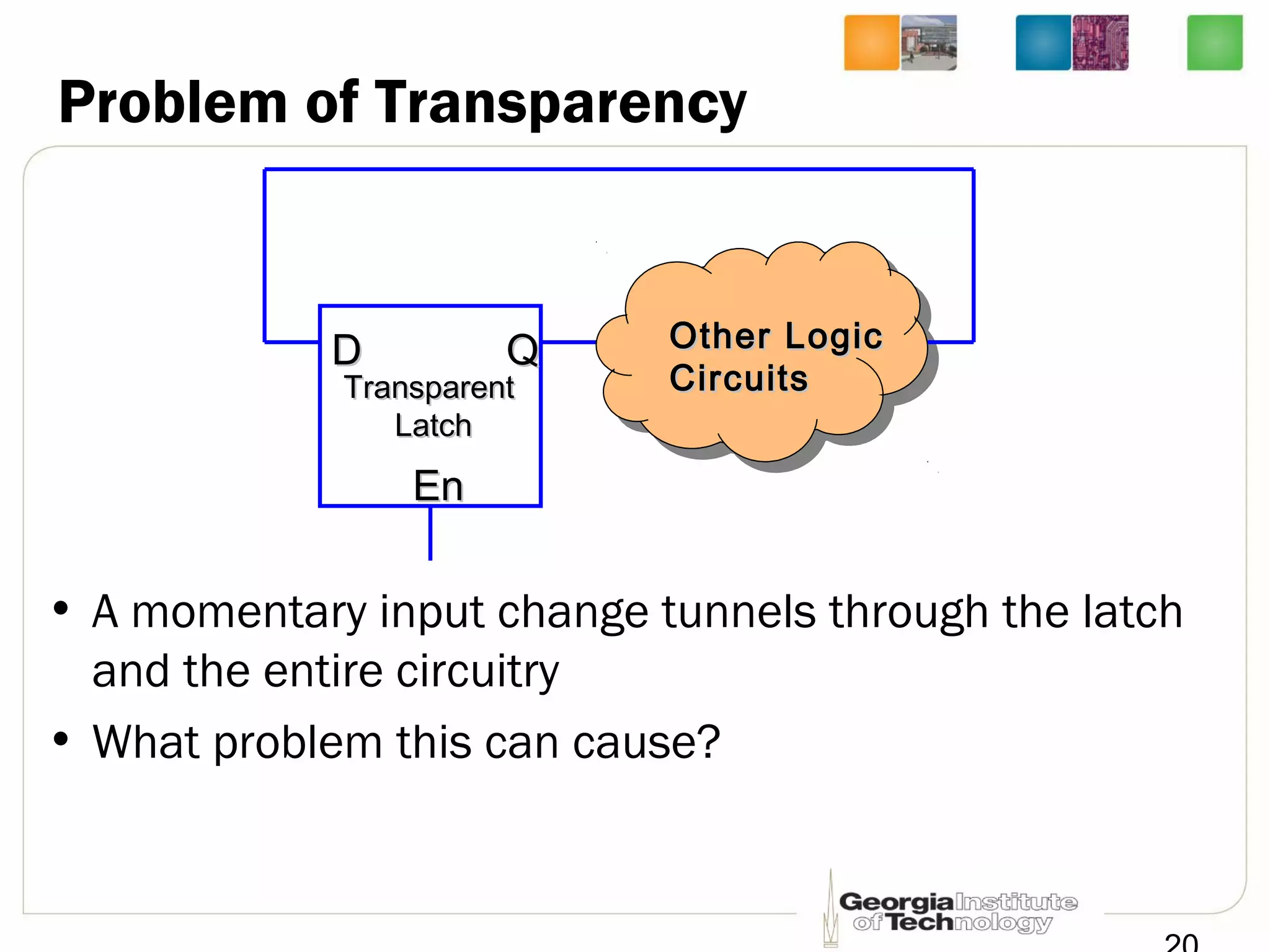
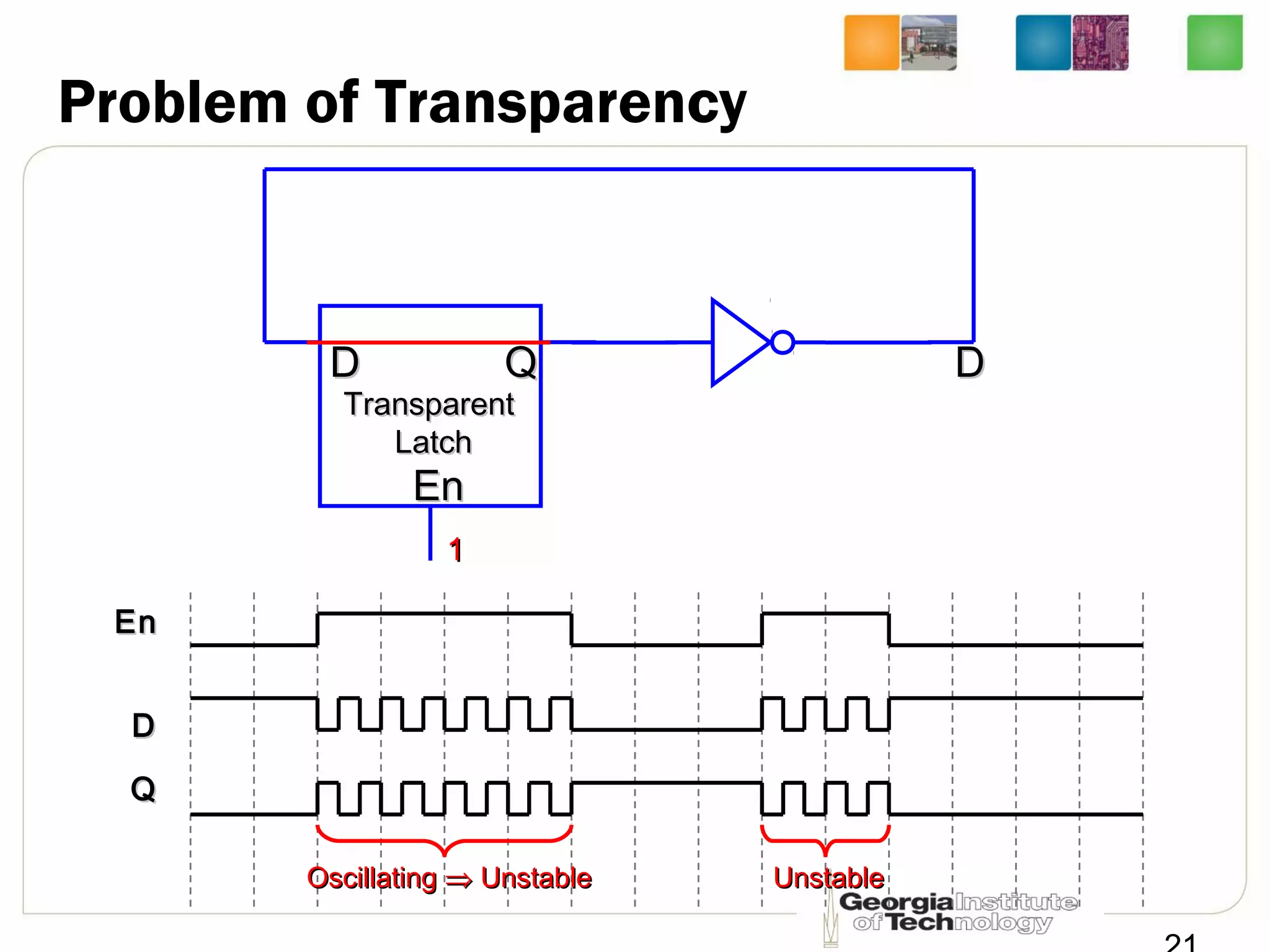
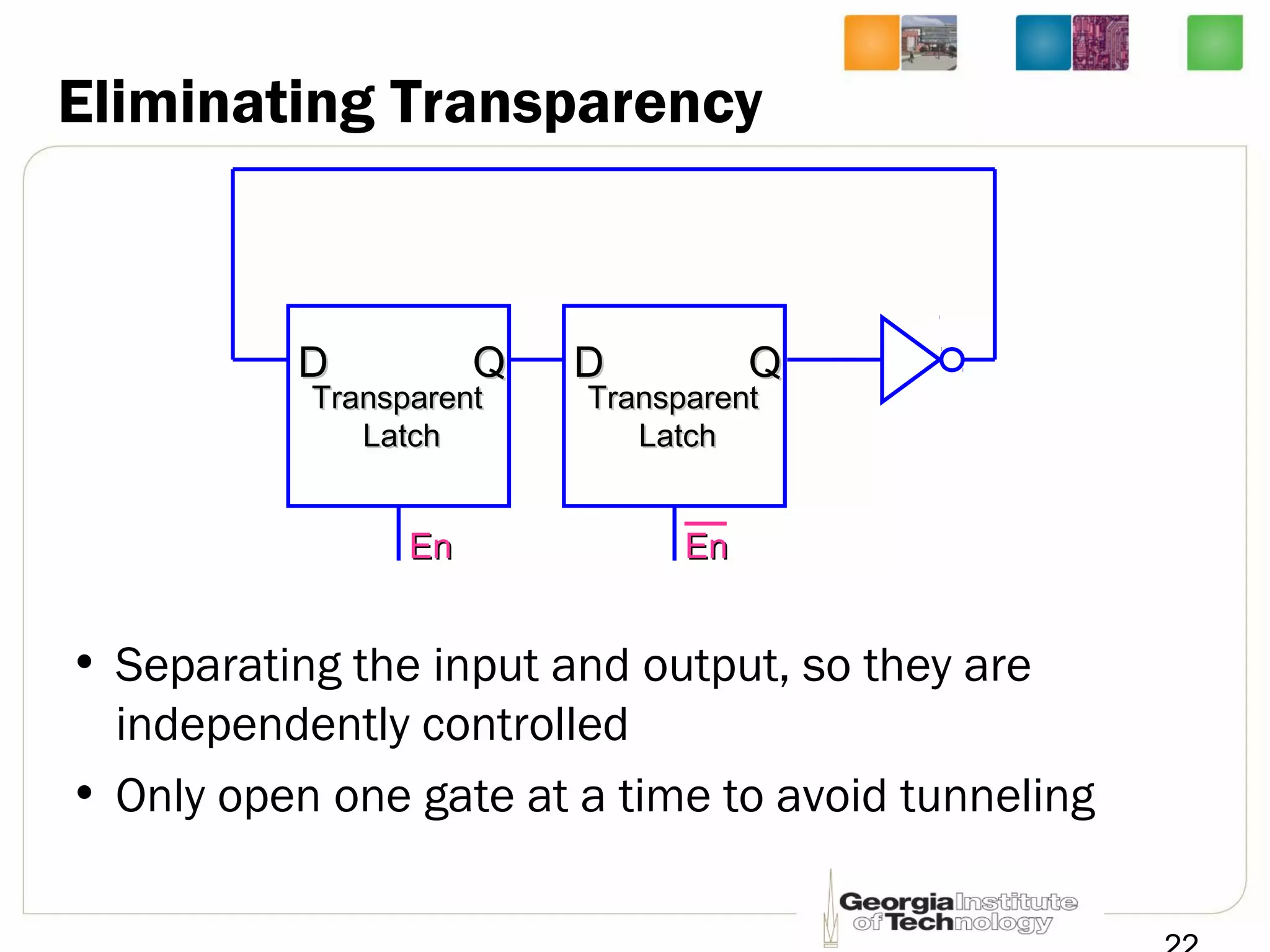
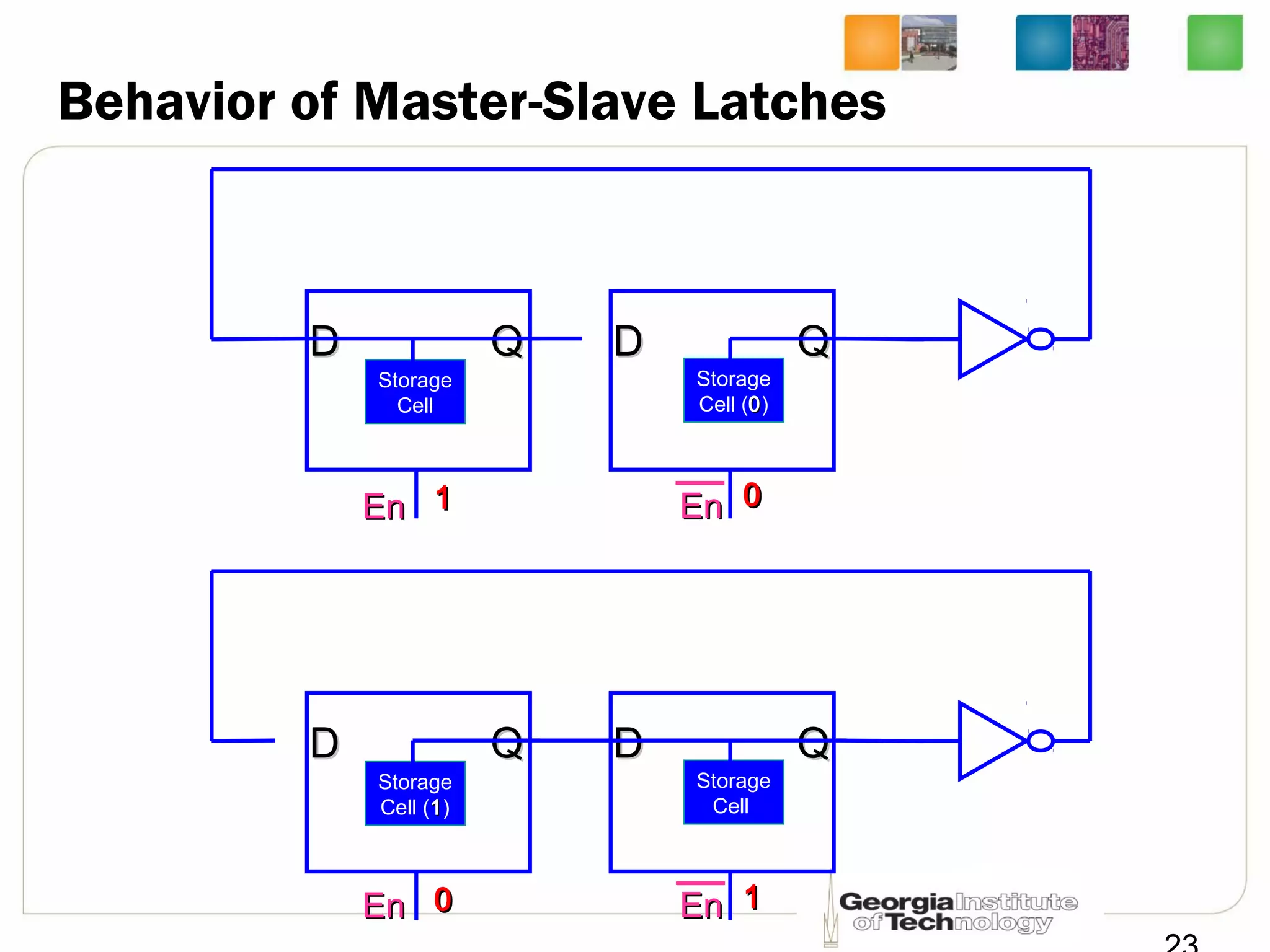
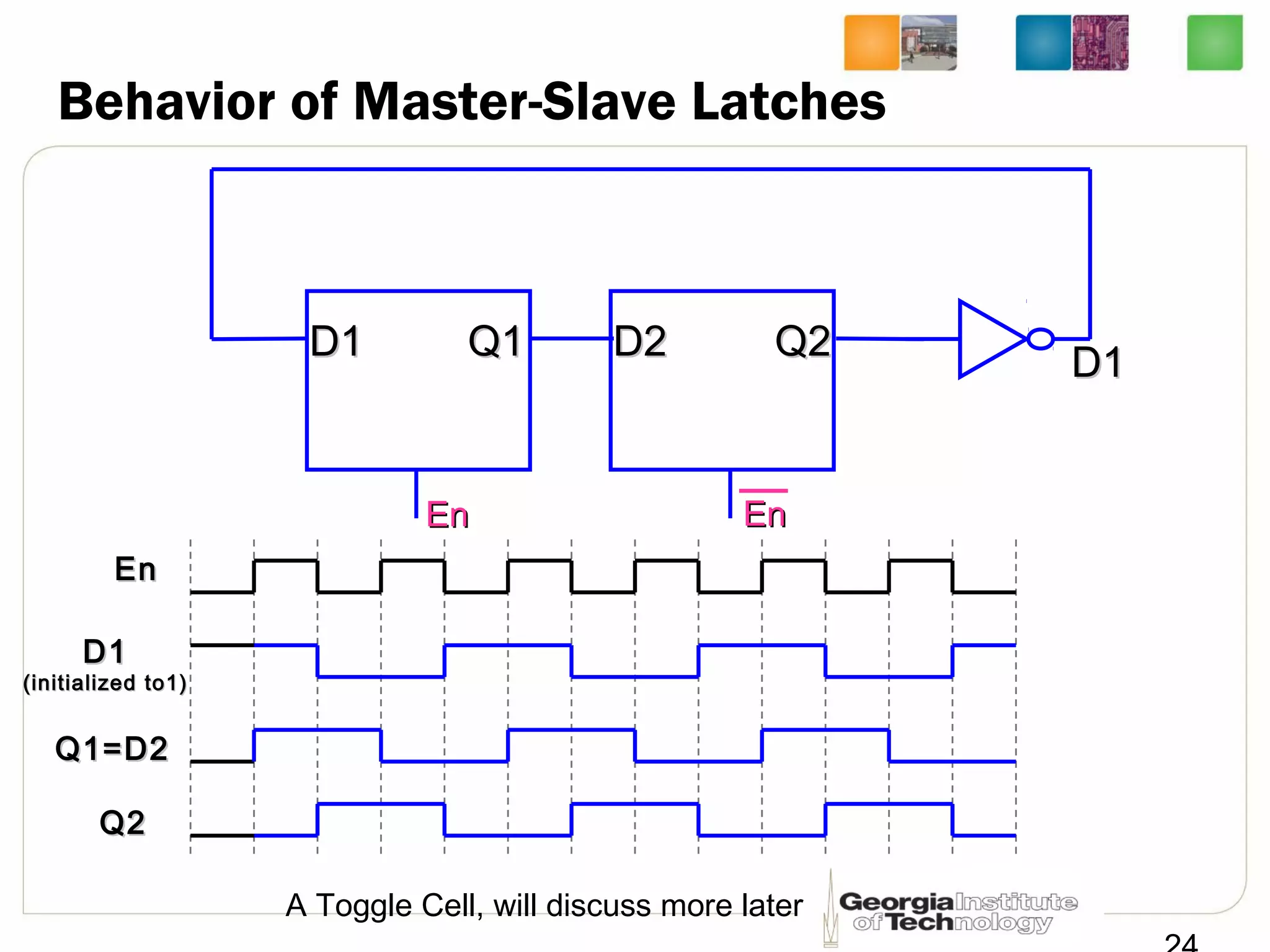
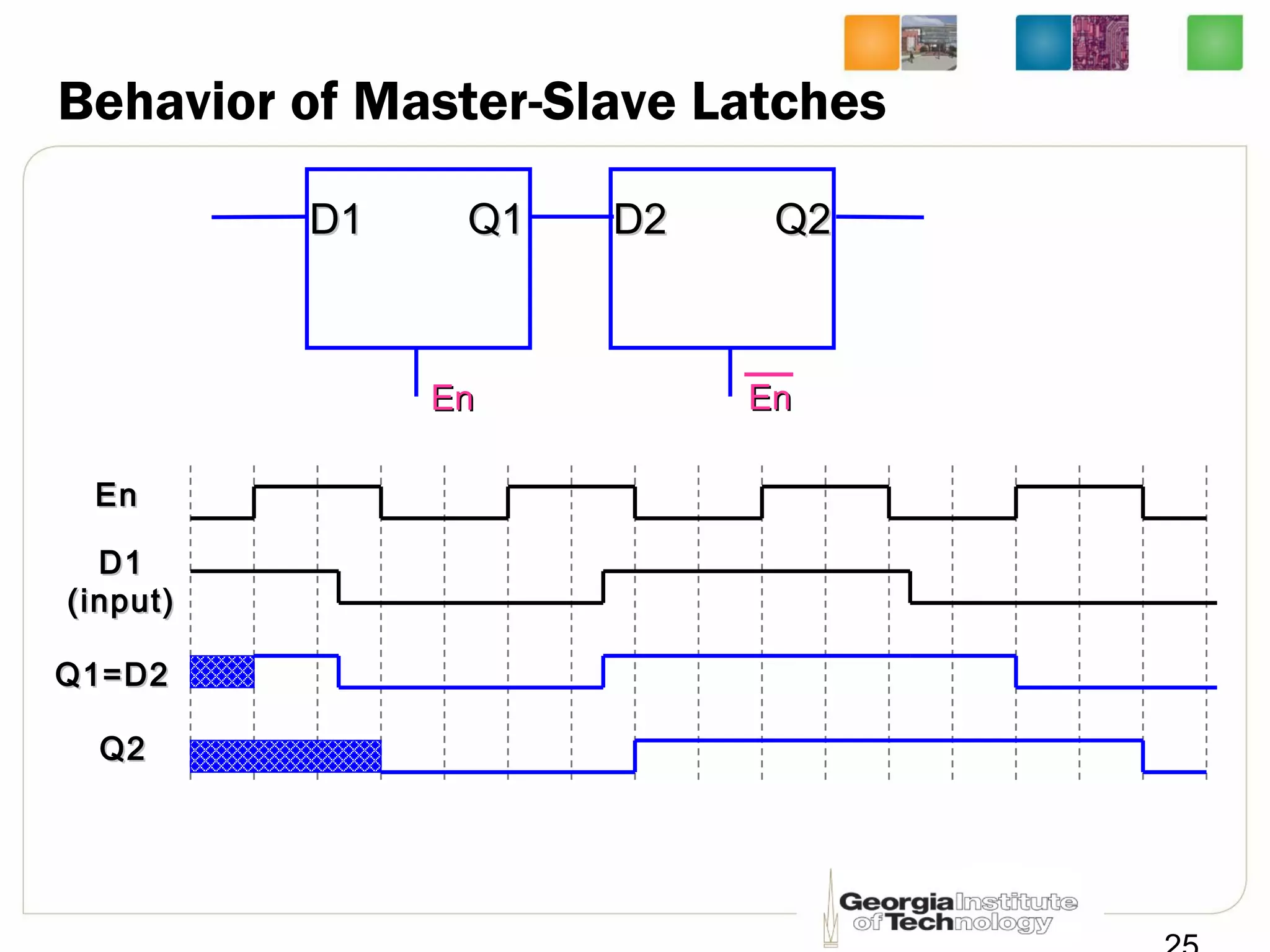
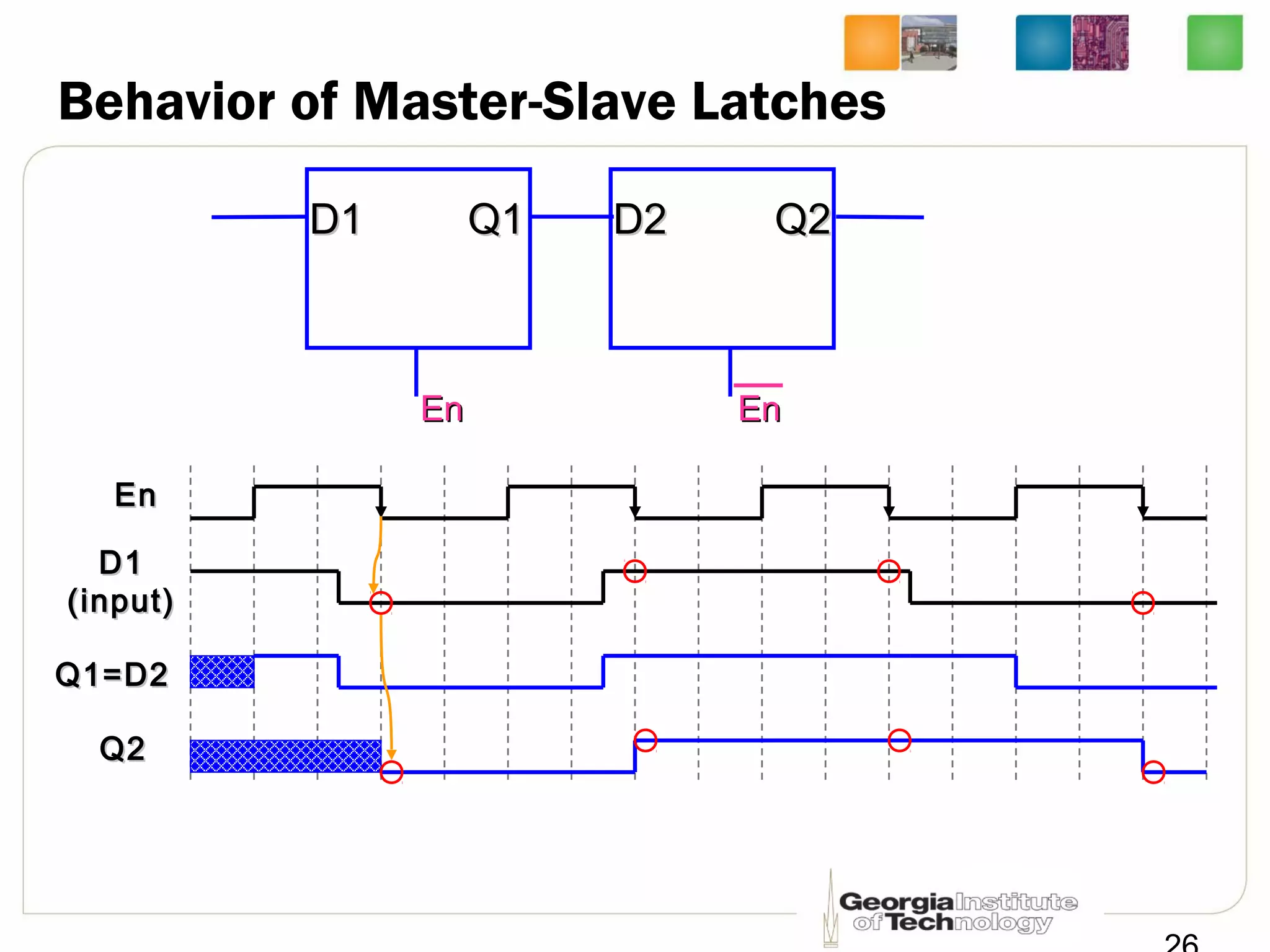
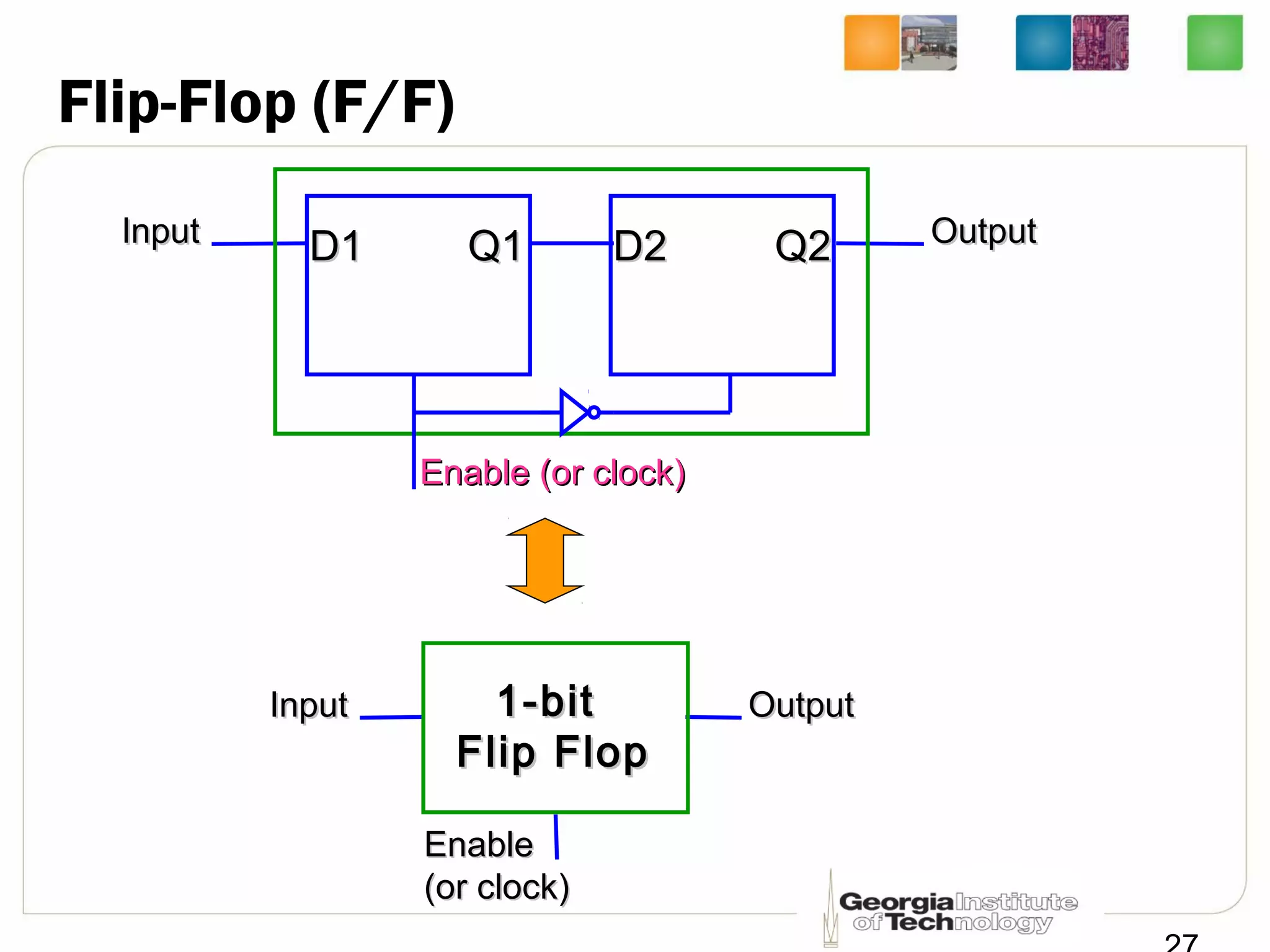
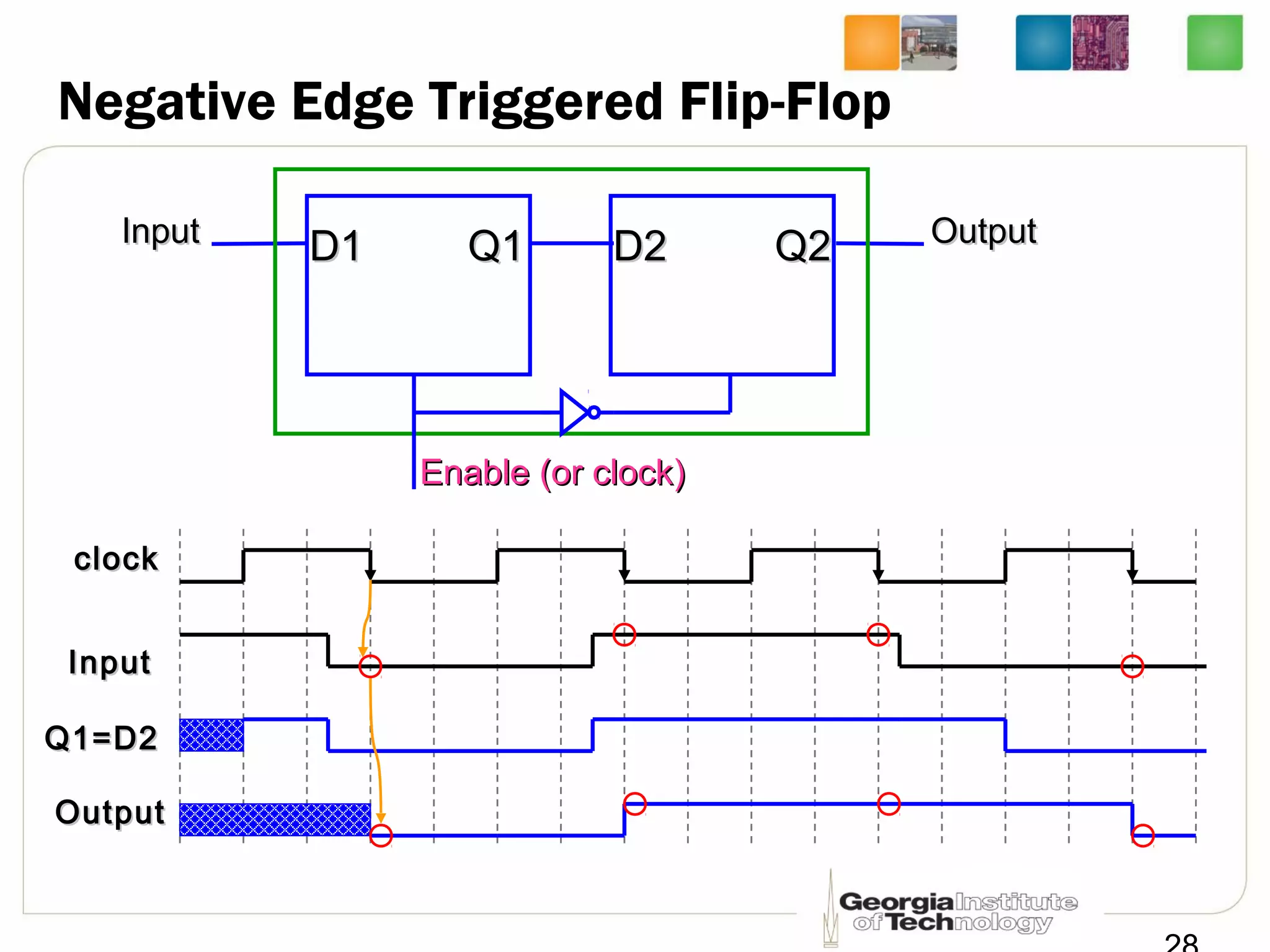
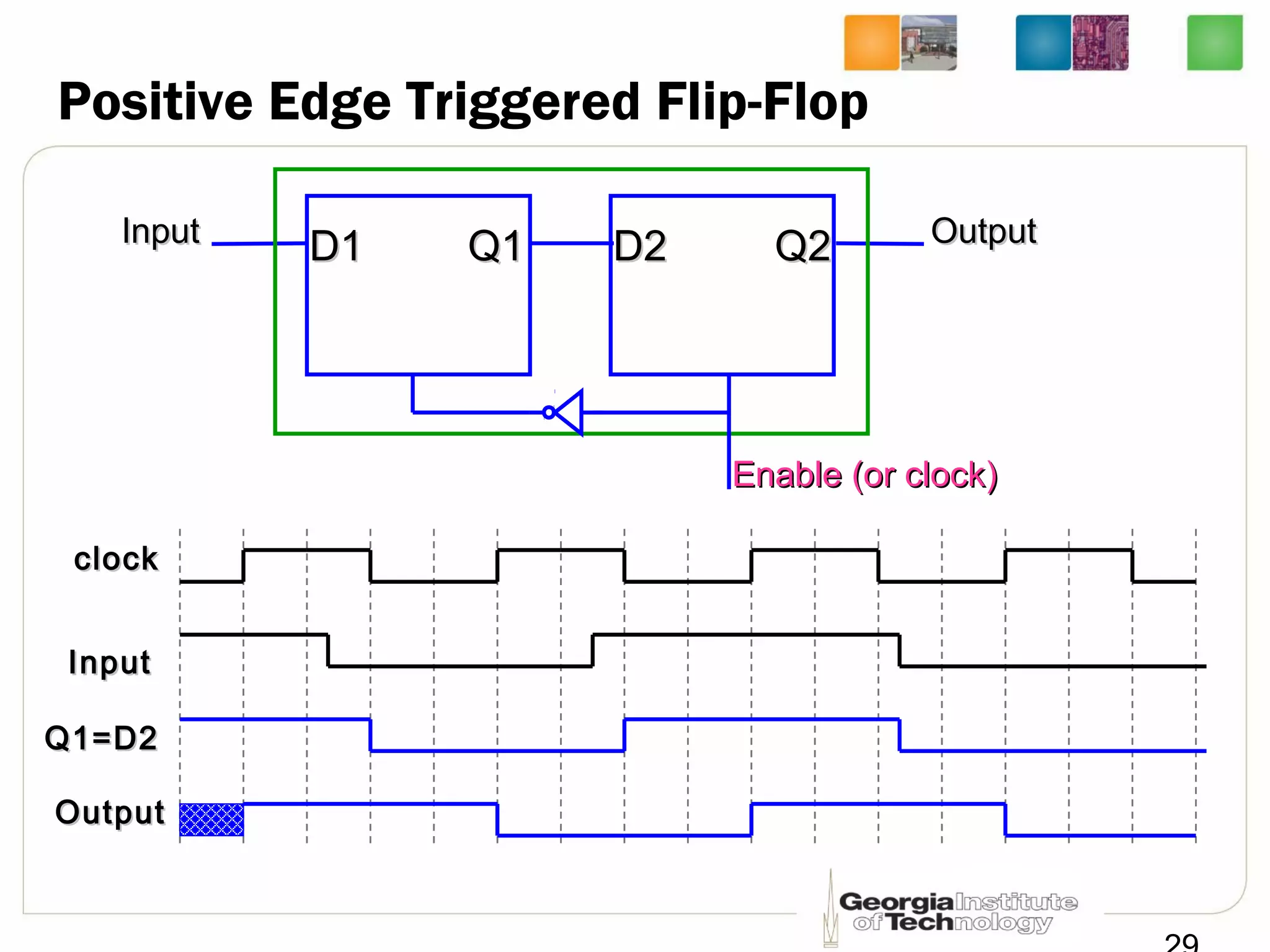
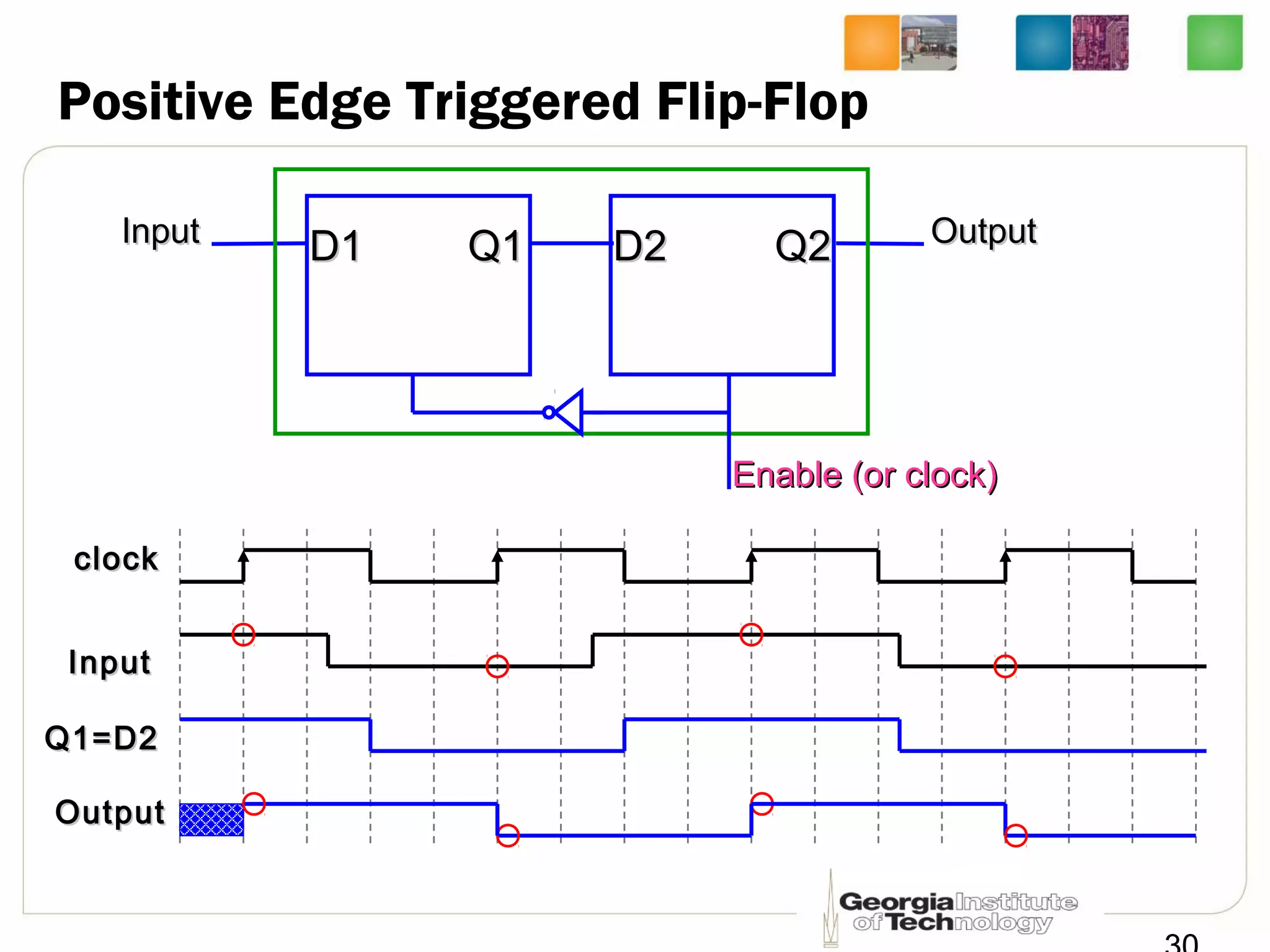
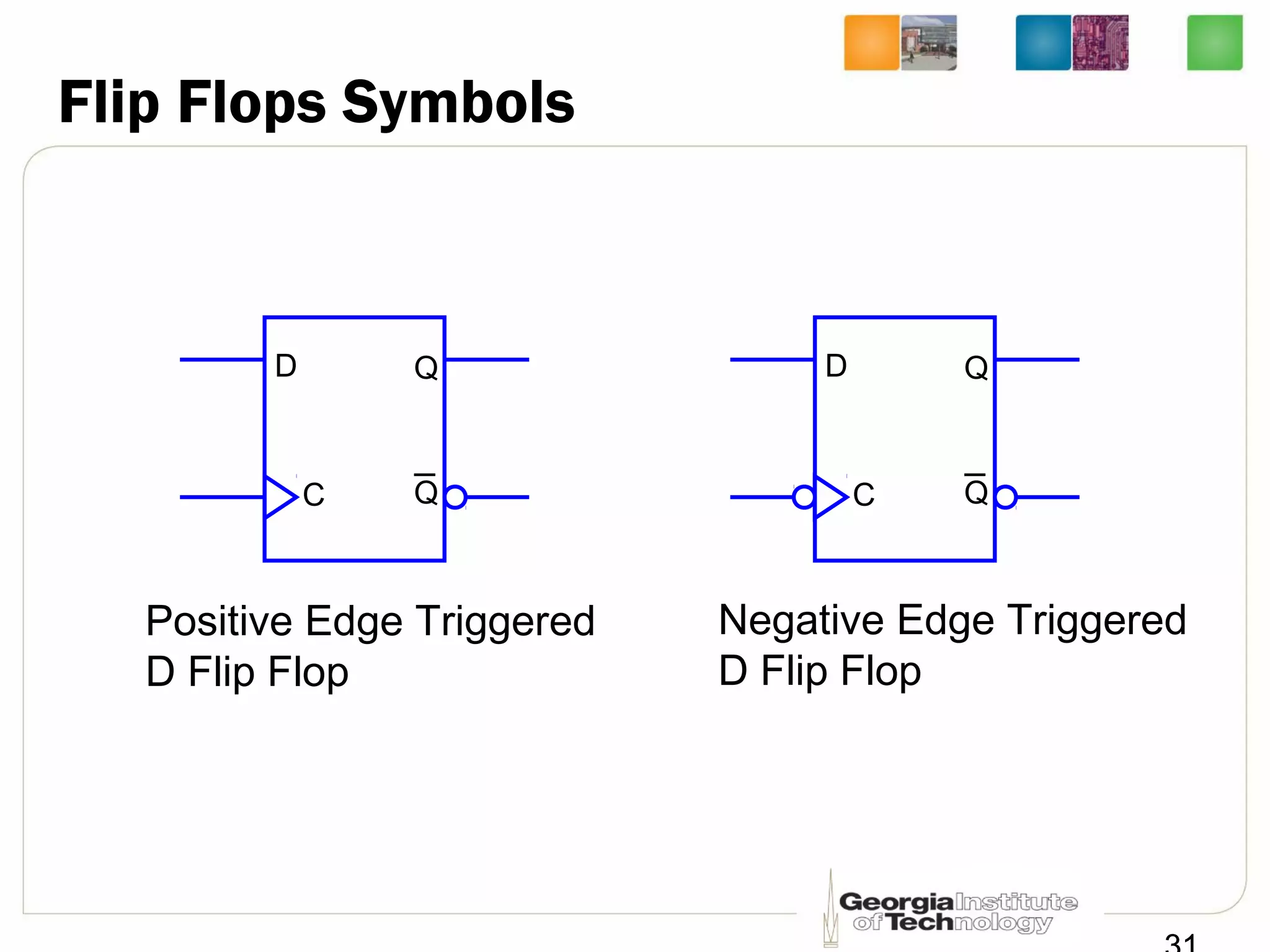
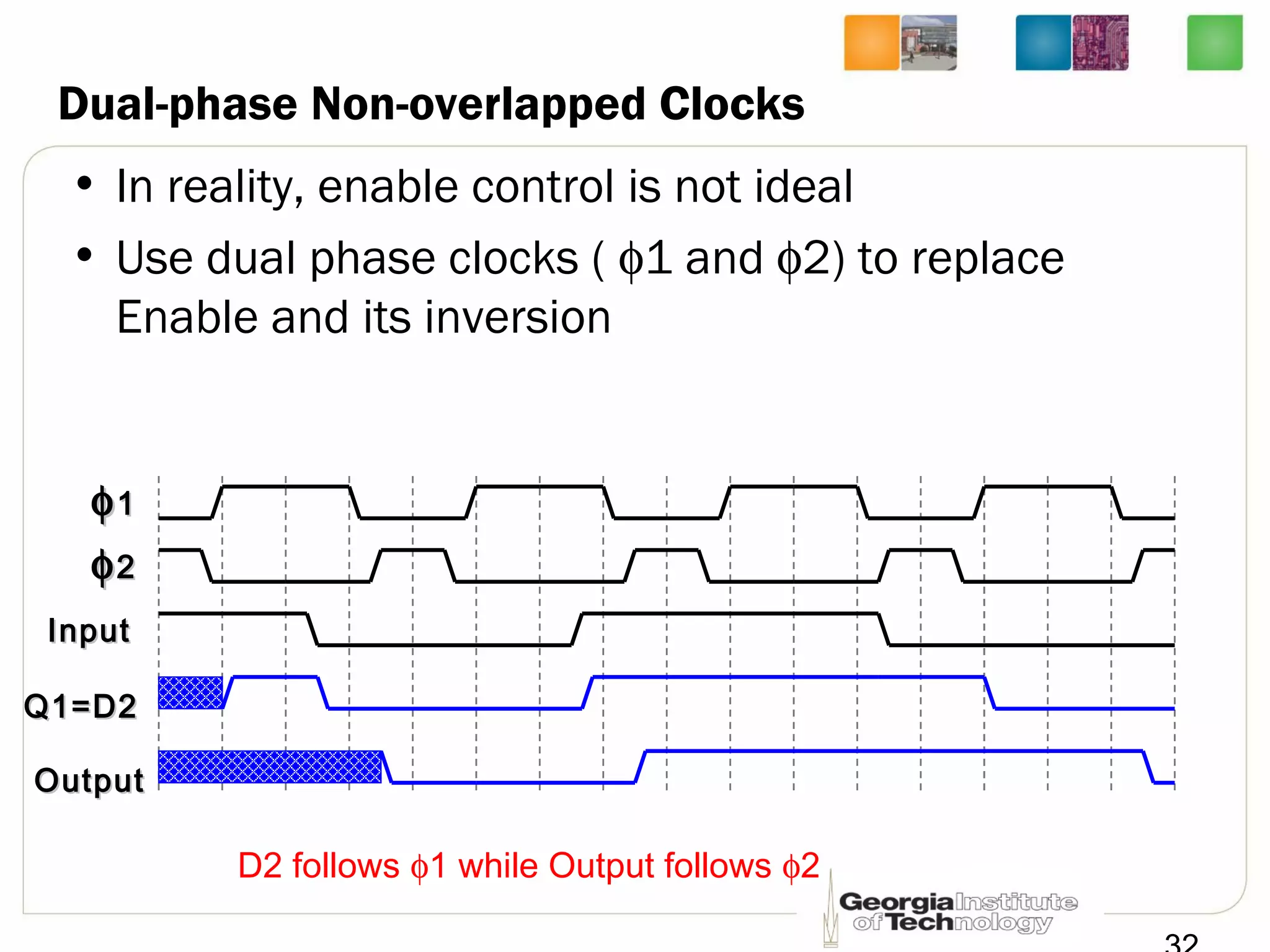
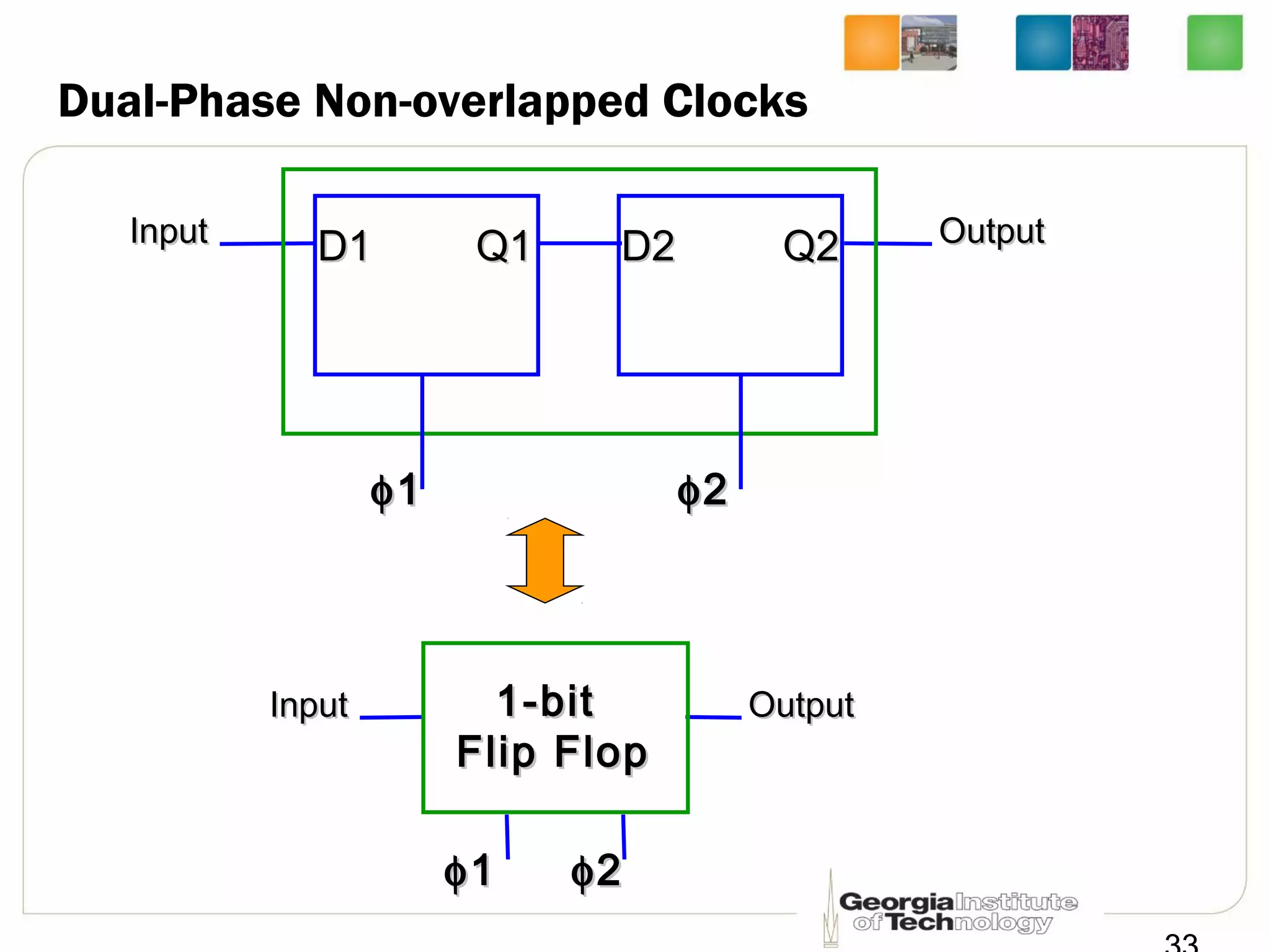
This document discusses sequential logic circuits, which differ from combinational logic circuits in that they have state information stored in memory elements like flip-flops. The output of a sequential circuit depends on both the inputs and the present state. Common types of sequential elements discussed include SR latches, D latches, and edge-triggered flip-flops. Master-slave configurations are used to avoid problems with transparency in latches. Dual-phase non-overlapping clocks are introduced to control the transfer of data between latches in a flip-flop.
More Related Content
Similar to Lec14 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Sequential Logic
Lec14 Intro to Computer Engineering by Hsien-Hsin Sean Lee Georgia Tech -- Sequential Logic
- 1. ECE2030 Introduction to ComputerEngineering Lecture 14: Sequential Logic Circuits Prof. Hsien-Hsin Sean LeeProf. Hsien-Hsin Sean Lee School of Electrical and Computer EngineeringSchool of Electrical and Computer Engineering Georgia TechGeorgia Tech
- 2. Sequential Logic Circuits •Sequential circuits – Combinational logic circuits – State information (stored in memory) • Output is a function of inputs and present state • Can be synchronous or asynchronous Combinational circuits inputs outputs Storage Element delaydelay PresentPresent StateState NextNext StateState Controller by a periodic clock or an event trigger
- 3. State machine example ATV channel control CH 2CH 2 CH 3CH 3 CH 1CH 1 0 0 1 1 1 0
- 4. Sequential Logic Circuits •Synchronous Circuits use clock pulse to synchronize • For a typical synchronous design, data are latched into the storage upon clock transition (edge-triggered) Combinational circuits inputs outputs Storage Element PresentPresent StateState NextNext StateState clock
- 5. Closed-Loop Logic forStoring Information 10 A buffer Tpd Tpd XX =
- 6.
- 7. SR Latch S RQ QN 0 0 Q Q 0 1 0 1 1 0 1 0 1 1 0 0 SS QQ QQNN RR Reset Set Undefined No Change
- 8. SR Latch S RQ QN 0 0 1 1 0 1 1 0 1 0 0 1 1 1 Q Q RR QQ QQNN SS Reset Set Undefined No Change
- 9. SR Latch w/Control C S R Q QN 0 X X Q Q 1 0 0 Q Q 1 0 1 0 1 1 1 0 1 0 1 1 1 1 1 QQ QQNN RR CC SS Reset Set Undefined No Change No Change
- 10. Issue of anSR Latch or SR Latch SS QQ QQNN RR SS RR S R Q QN 0 0 Q Q 0 1 0 1 1 0 1 0 1 1 0 0 QQ QQNN Race, and UnstableRace, and Unstable
- 11. D Latch QQ QQNN CC DD C DQ QN 0 X Q Q 1 0 0 1 1 1 1 0
- 12. D Latch Keeping Data for Read QQ QQ
- 13. D Latch Writing Data DD DD QQ QQ
- 14. 10T D Latchw/ Transmission Gates DD EnEn EnEn EnEn QQ QQ
- 15. 10T D Latchw/ Transmission Gates DD En=1En=1 EnEn QQ QQ DD Writing Data DD DDEnEn
- 16. 10T D Latchw/ Transmission Gates D_newD_new En=0En=0 EnEn QQ QQ Writing Data DD DD DD EnEn
- 17. D Latch Symbol DD EnEn QQ QQ EnD Q Q 0 X NC NC 1 0 0 1 1 1 1 0 NC: No Change
- 18. Latch is Transparent •D Latch is called “transparent” or “level sensitive” • Output follows input instantaneously EnEn DD QQ QQ Transparent
- 19. Transparency Property DD EnEn QQ Transparent Latch DD EnEn QQ Storage Cell 00 DD EnEn QQ Storage Cell 11 Latch actslike a WireLatch acts like a Wire
- 20. Problem of Transparency •A momentary input change tunnels through the latch and the entire circuitry • What problem this can cause? DD EnEn QQ TransparentTransparent LatchLatch Other LogicOther Logic CircuitsCircuits
- 21. Problem of Transparency EnEn TransparentTransparent LatchLatch 11 DDQQ DD EnEn DD QQ OscillatingOscillating ⇒⇒ UnstableUnstable UnstableUnstable
- 22. Eliminating Transparency • Separatingthe input and output, so they are independently controlled • Only open one gate at a time to avoid tunneling EnEn TransparentTransparent LatchLatch DD QQ EnEn TransparentTransparent LatchLatch DD QQ
- 23. Behavior of Master-SlaveLatches EnEn DD QQ EnEn DD QQ 11 00 Storage Cell Storage Cell (00) EnEn DD QQ EnEn DD QQ 00 11 Storage Cell (11) Storage Cell
- 24. Behavior of Master-SlaveLatches EnEn D1D1 Q1Q1 EnEn D2D2 Q2Q2 EnEn D1D1 (initialized to1)(initialized to1) D1D1 Q1=D2Q1=D2 Q2Q2 A Toggle Cell, will discuss more later
- 25. Behavior of Master-SlaveLatches EnEn D1D1 Q1Q1 EnEn D2D2 Q2Q2 EnEn D1D1 (input)(input) Q1=D2Q1=D2 Q2Q2
- 26. Behavior of Master-SlaveLatches EnEn D1D1 Q1Q1 EnEn D2D2 Q2Q2 EnEn Q1=D2Q1=D2 Q2Q2 D1D1 (input)(input)
- 27. Flip-Flop (F/F) D1D1 Q1Q1D2D2 Q2Q2 Enable (or clock)Enable (or clock) InputInput OutputOutput EnableEnable (or clock)(or clock) InputInput OutputOutput1-bit1-bit Flip FlopFlip Flop
- 28. Negative Edge TriggeredFlip-Flop D1D1 Q1Q1 D2D2 Q2Q2 clockclock InputInput Q1=D2Q1=D2 OutputOutput Enable (or clock)Enable (or clock) InputInput OutputOutput
- 29. Positive Edge TriggeredFlip-Flop D1D1 Q1Q1 D2D2 Q2Q2 clockclock Q1=D2Q1=D2 Enable (or clock)Enable (or clock) InputInput OutputOutput InputInput OutputOutput
- 30. Positive Edge TriggeredFlip-Flop D1D1 Q1Q1 D2D2 Q2Q2 clockclock Q1=D2Q1=D2 Enable (or clock)Enable (or clock) InputInput OutputOutput InputInput OutputOutput
- 31. Flip Flops Symbols D C Q Q D C Q Q PositiveEdge Triggered D Flip Flop Negative Edge Triggered D Flip Flop
- 32. Dual-phase Non-overlapped Clocks •In reality, enable control is not ideal • Use dual phase clocks ( φ1 and φ2) to replace Enable and its inversion φφ11 Q1=D2Q1=D2 InputInput OutputOutput φφ22 D2 follows φ1 while Output follows φ2
- 33. Dual-Phase Non-overlapped Clocks D1D1Q1Q1 D2D2 Q2Q2InputInput OutputOutput InputInput OutputOutput1-bit1-bit Flip FlopFlip Flop φφ11 φφ22 φφ11 φφ22