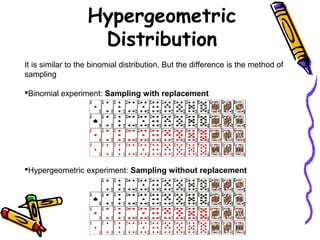
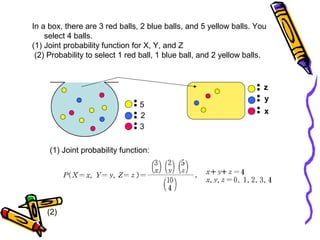
The document discusses the hypergeometric distribution, which describes the probability of successes in draws without replacement from a finite population. It provides the formula for the hypergeometric distribution and compares it to the binomial distribution. Examples are given to demonstrate how to calculate probabilities of various outcomes using the hypergeometric distribution formula.

1. HYPERGEOMETRIC
DISTRIBUTION
PREPARED BY :
Mohammad Nouman

2. 2
Hypergeometric
Distribution
Formula
Definition
In probability theory and statistics, the
hypergeometric distribution is a discrete probability
distribution that describes the probability of successes
in draws, without replacement.

3. Hypergeometric
Distribution
Mean And Variance
Hypergeometric Distribution Binomial Distribution
N
S
N
nN
N
Sn
XVar −⋅
−
−
⋅
⋅
= 1
1
)(
N
sn
XE
⋅
== )(µ
)1)()(()( ppnXVar −=

4. 4
Hypergeometric Distribution
characteristics
The hypergeometric distribution has the
following characteristics:
 There are only 2 possible outcomes.
 The probability of a success is not the same
on each trial without replacement, thus
events are not independent
 In which population is finite .
 Trials are dependent

5. Hypergeometric
Distribution
It is similar to the binomial distribution. But the difference is the method of
sampling
Binomial experiment: Sampling with replacement
Hypergeometric experiment: Sampling without replacement

6. 6
Hypergeometric
Distribution
Example 1
In PlayTime Toys, Inc.,
Five employees are selected at
random to form a committee
to meet with management
regarding shift starting
times. What is the
probability that four of the
five selected for the
committee belong to a union?
Union Employee 40
Not Union
Employee
10
Total Employee 50

7. 7
Hypergeometric
Distribution

8. Hypergeometric
Distribution
Example 2 :A carton contains light bulbs
What is the probability that, if a sample of six is chosen at
random from the carton of bulbs, x will be defective?
( ) ( )
( )24
6
21
6
3
)( xx
xXP −⋅
==
( ) ( )
( ) 40316.0)0( 24
6
21
6
3
0
=
⋅
==XP
That is no defective
Defective 3
Total 24

9. Hypergeometric
Distribution
(example continued)
( ) ( )
( ) 00988.0)3( 24
6
21
3
3
3
=
⋅
==XP
That is 3 will be defective.

10. EXAMPLE 3
In a bag containing
select 2 chips one after the other without
replacement.
Hypergeometric
Distribution
Red Chips 7
Blue Chips 5
Total Chips 12

11. Multivariate
Hypergeometric
Distribution
 X1 , X2 , X3 : Joint Probability Function

12. (1) Joint probability function:
5
2
3
z
y
x
(2)
In a box, there are 3 red balls, 2 blue balls, and 5 yellow balls. You
select 4 balls.
(1) Joint probability function for X, Y, and Z
(2) Probability to select 1 red ball, 1 blue ball, and 2 yellow balls.

13. Hypergeometric
Distribution
Example4:Suppose that a shipment contains
.If 7 items are selected at random without replacement , what is
the probability that at least 3 defective items will be obtained?
=≤−=≥ )2(1)3( XPXP [ ] 4267.0)2()1()0(1 =++− PPP
( ) ( )
( )
( ) ( )
( )
( ) ( )
( ) 3916.0)2(
1631.0)1(
0186.0)0(
15
7
10
5
5
2
15
7
10
6
5
1
15
7
10
7
5
0
=
⋅
=
=
⋅
=
=
⋅
=
P
P
P
Defective Items Non Defective Item Total
5 10 15

14. EXAMPLE 5
4 3 10 4 5 3
10 5
4 3 6 2
10 5
( )( )
(3)
( )( ) 4(15)
.238
252
C C
P
C
C C
C
− −
=
= = =
The National Air Safety Board has
Safety Board will only be able to investigate five of the
violations. What is the probability that three of five
violations randomly selected to be investigated are
actually violations?
List Reported Safety Violation 10
Actual Violation 4
Hypergeometric
Distribution

15. 15
Hypergeometric Distribution
Example 1
In PlayTime Toys, Inc.,
Five employees are selected at
random to form a committee
to meet with management
regarding shift starting
times. What is the
probability that four of the
five selected for the
committee belong to a union?
Union Employee 40
Not Union
Employee
10
Total Employee 50

16. 16
Hypergeometric
Distribution
Excel
Use function HYPERGEOM.DIST(x,n,S,N)

17. Any Question…?