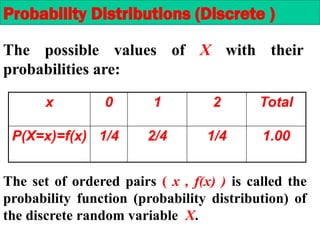
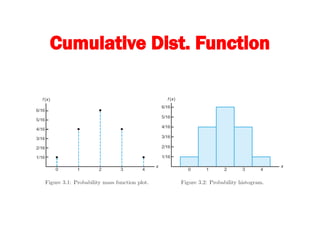
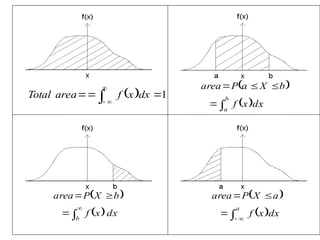
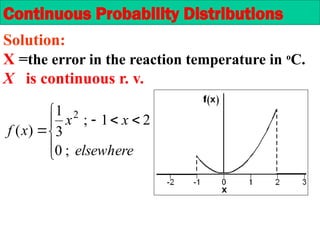
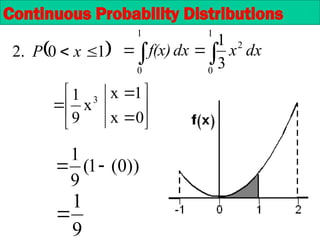
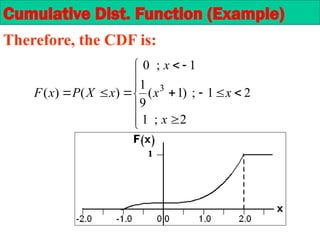
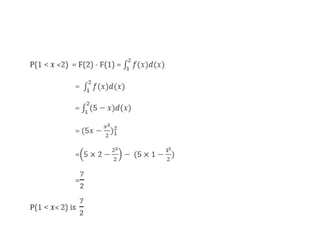The document provides an overview of random variables and probability distributions, emphasizing the distinction between discrete and continuous random variables. It includes examples and definitions of probability functions, mass functions, and cumulative distribution functions for different random variables. The document also discusses methods for calculating probabilities and the characteristics of distributions.