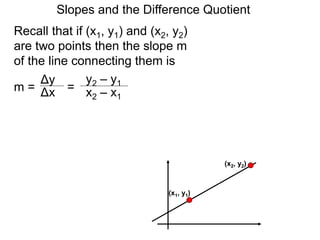
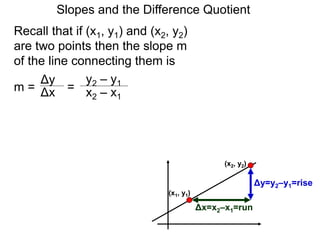
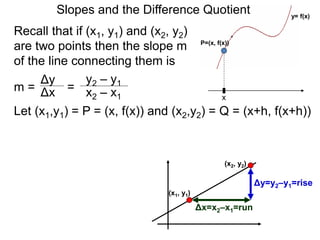
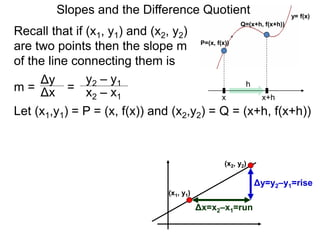
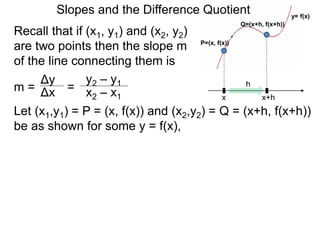
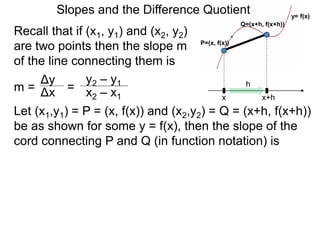
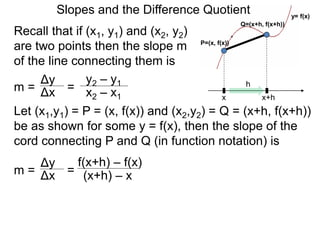
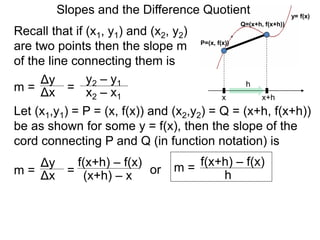
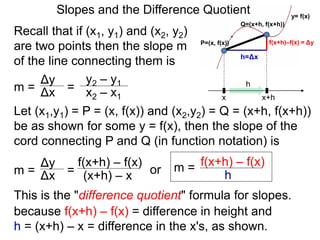
The document discusses the difference quotient formula for calculating the slope between two points (x1,y1) and (x2,y2) on a function y=f(x). It shows that the slope m is equal to (f(x+h)-f(x))/h, where h is the difference between x1 and x2. This "difference quotient" formula allows slopes to be calculated from the values of a function at two nearby points. Examples are given of simplifying the difference quotient for quadratic and rational functions.

1. Slopes and the Difference Quotient

2. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
Δy
m =
y2 – y1
= x2 – x1Δx
Slopes and the Difference Quotient
(x1, y1)
(x2, y2)

3. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
Δy
m =
y2 – y1
= x2 – x1Δx
Slopes and the Difference Quotient
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run

4. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x))
x
P=(x, f(x))
Slopes and the Difference Quotient y= f(x)
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run

5. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
Slopes and the Difference Quotient y= f(x)
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run

6. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
Slopes and the Difference Quotient y= f(x)
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
h

7. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x),
Slopes and the Difference Quotient y= f(x)
h

8. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Slopes and the Difference Quotient y= f(x)
h

9. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – xΔx
Slopes and the Difference Quotient y= f(x)
h

10. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – xΔx or m = f(x+h) – f(x)
h
Slopes and the Difference Quotient y= f(x)
h

11. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – xΔx or m = f(x+h) – f(x)
h
This is the "difference quotient" formula for slopes
Slopes and the Difference Quotient y= f(x)
h

12. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – xΔx or m = f(x+h) – f(x)
h
f(x+h)–f(x) = Δy
because f(x+h) – f(x) = difference in height
This is the "difference quotient" formula for slopes
Slopes and the Difference Quotient y= f(x)

13. Recall that if (x1, y1) and (x2, y2)
are two points then the slope m
of the line connecting them is
x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
Δy
m =
y2 – y1
= x2 – x1Δx
Let (x1,y1) = P = (x, f(x)) and (x2,y2) = Q = (x+h, f(x+h))
be as shown for some y = f(x), then the slope of the
cord connecting P and Q (in function notation) is
Δy
m =
f(x+h) – f(x)
= (x+h) – xΔx or m = f(x+h) – f(x)
h
h=Δx
f(x+h)–f(x) = Δy
because f(x+h) – f(x) = difference in height and
h = (x+h) – x = difference in the x's, as shown.
This is the "difference quotient" formula for slopes.
Slopes and the Difference Quotient y= f(x)
h

14. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
y= f(x)
h

15. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
y= f(x)
h

16. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
Examples of the algebra for manipulating this formula
are given below.
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
y= f(x)
h

17. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
Examples of the algebra for manipulating this formula
are given below.
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
Example A. (Quadratics) Given f(x) = x2 – 2x + 2,
f(x+h) – f(x)
h .simplify its difference–quotient
y= f(x)
h

18. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
Examples of the algebra for manipulating this formula
are given below.
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
Example A. (Quadratics) Given f(x) = x2 – 2x + 2,
f(x+h) – f(x)
h =
f(x+h) – f(x)
h .simplify its difference–quotient
y= f(x)
h

19. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
Examples of the algebra for manipulating this formula
are given below.
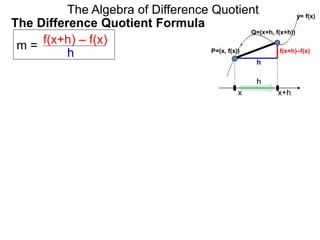
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
Example A. (Quadratics) Given f(x) = x2 – 2x + 2,
f(x+h) – f(x)
h =
(x+h)2 – 2(x+h) + 2 – [ x2 – 2x + 2]
h
f(x+h) – f(x)
h .simplify its difference–quotient
y= f(x)
h

20. x
P=(x, f(x))
x+h
Q=(x+h, f(x+h))
The goal of “simplifying”
the difference–quotient formula
is to eliminate the h in the denominator.
Examples of the algebra for manipulating this formula
are given below.
m = f(x+h) – f(x)
h
h
f(x+h)–f(x)
The Algebra of Difference Quotient
The Difference Quotient Formula
Example A. (Quadratics) Given f(x) = x2 – 2x + 2,
f(x+h) – f(x)
h =
(x+h)2 – 2(x+h) + 2 – [ x2 – 2x + 2]
h
2xh – 2h + h2
h
= 2x – 2 + h.=
f(x+h) – f(x)
h .simplify its difference–quotient
y= f(x)
http://www.slideshare.net/math123
a/4-7polynomial-operationsvertical
h

21. The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
The Algebra of Difference Quotient

22. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
The Algebra of Difference Quotient

23. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=

24. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
–3 – (x + h)
2
3 – x
2
h
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=

25. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
–3 – (x + h)
2
3 – x
2
h
(3 – x – h) (3 – x)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3 – x – h) (3 – x)

26. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
–3 – (x + h)
2
3 – x
2
h
(3 – x – h) (3 – x)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3 – x – h) (3 – x)
(3 – x – h)(3 – x)

27. Example B. (Rational Functions I)
Simplify the difference quotient of f(x) =
The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
3 – x
2
–3 – (x + h)
2
3 – x
2
h
(3 – x – h) (3 – x)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3 – x – h) (3 – x)
(3 – x – h)(3 – x)
2(3 – x) – 2(3 – x – h)
h(3 – x – h) (3 – x)
=
Warning: It’s illegal to cancel the ( )’s,
we have to simplify the numerator,
simplify

28. The algebra for simplifying the difference quotient of
rational functions is the algebra for simplifying
complex fractions. To simplify a complex fraction,
use the LCD to clear all denominators.
–3 – (x + h)
2
3 – x
2
h
(3 – x – h) (3 – x)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3 – x – h) (3 – x)
(3 – x – h)
2(3 – x) – 2(3 – x – h)
h(3 – x – h) (3 – x)
= simplify
2h
h(3 – x – h) (3 – x)=
2
(3 – x – h) (3 – x)=
Example B. (Rational Functions I)
Simplify the difference quotient of f(x) = 3 – x
2
(3 – x)

29. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
The Algebra of Difference Quotient
3x + 1
2x – 3

30. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
3x + 1
2x – 3

31. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3

32. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
(3x + 3h + 1)(3x + 1)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3
(3x + 3h + 1)(3x + 1)

33. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
(3x + 3h + 1)(3x + 1)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3x + 3h + 1)(3x + 1)
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3
(3x + 3h + 1)(3x + 1)

34. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
(3x + 3h + 1)(3x + 1)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3x + 3h + 1)(3x + 1)
h(3x + 3h + 1)(3x + 1)
=
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3
(3x + 3h + 1)(3x + 1)
(2x + 2h – 3)(3x + 1) – (2x – 3)(3x + 3h + 1)

35. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
(3x + 3h + 1)(3x + 1)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3x + 3h + 1)(3x + 1)
h(3x + 3h + 1)(3x + 1)
=
11h
=
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3
(3x + 3h + 1)(3x + 1)
(2x + 2h – 3)(3x + 1) – (2x – 3)(3x + 3h + 1)
h(3x + 3h + 1)(3x + 1)

36. Example C. (Rational Functions II)
Simplify the difference quotient of f(x) =
(3x + 3h + 1)(3x + 1)
The Algebra of Difference Quotient
f(x+h) – f(x)
h
=
(3x + 3h + 1)(3x + 1)
h(3x + 3h + 1)(3x + 1)
=
11h
=
http://www.slideshare.net/math123b/2-5-complex-fractions
3x + 1
2x – 3
–
3(x + h) + 1 3x + 1
2x – 3
h
2(x + h) – 3
(3x + 3h + 1)(3x + 1)
(2x + 2h – 3)(3x + 1) – (2x – 3)(3x + 3h + 1)
h(3x + 3h + 1)(3x + 1)
11
=
(3x + 3h + 1)(3x + 1)

37. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
The Algebra of Difference Quotient

38. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =

39. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
h
2(x + h) – 1 – 2x – 1
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =
f(x + h) – f(x)
h
=

40. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
h
2(x + h) – 1 – 2x – 1
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =
f(x + h) – f(x)
h
=
(2x + 2h –1 + 2x – 1)
(2x + 2h –1 + 2x – 1)

41. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
h
2(x + h) – 1 – 2x – 1
=
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =
f(x + h) – f(x)
h
=
(2x + 2h –1 + 2x – 1)
(2x + 2h –1 + 2x – 1)
(2x + 2h –1)2 – (2x – 1)2
h(2x + 2h –1 + 2x – 1)

42. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
h
2(x + h) – 1 – 2x – 1
=
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =
f(x + h) – f(x)
h
=
(2x + 2h –1 + 2x – 1)
(2x + 2h –1 + 2x – 1)
(2x + 2h –1)2 – (2x – 1)2
h(2x + 2h –1 + 2x – 1)
=
(2x + 2h –1) – (2x – 1)
h(2x + 2h –1 + 2x – 1)

43. To rationalize square–root radicals in expressions
we use the formula (x – y)(x + y) = x2 – y2 and
(x + y) and (x – y) are called conjugates.
h
2(x + h) – 1 – 2x – 1
=
2x – 1
The Algebra of Difference Quotient
Example D. (Square–root Functions I)
Simplify the difference quotient of f(x) =
f(x + h) – f(x)
h
=
(2x + 2h –1 + 2x – 1)
(2x + 2h –1 + 2x – 1)
(2x + 2h –1)2 – (2x – 1)2
h(2x + 2h –1 + 2x – 1)
=
(2x + 2h –1) – (2x – 1)
h(2x + 2h –1 + 2x – 1)
= 2h
h(2x + 2h –1 + 2x – 1)
= 2
(2x + 2h –1 + 2x – 1)
http://www.slideshare.net/math123b/2-5-complex-fractions

44. We will see in calculus that the above algebra extend
the concept of “the slope of a line” to
“varying slopes of a curve”. The ones we did in turn
give the bases for general approaches for computing
“slopes for curves”.
The Algebra of Difference Quotient

45. Simplify the difference quotient of the following
functions by removing the h in the denominator.
Quadratic Functions:
1. f(x) = x2 – 2 2. f(x) = x2 – 2x + 5
3. f(x) = –x2 + 2x + 3 4. f(x) = –3x2 – 2x – 3
5 f(x) = ax2 + bx + c
Rational Functions:
1. f(x) =
x – 2
3 2. f(x) =
2 – 3x
4 3. f(x) =
x – 2
3 – x
4. f(x) =
2x – 3
1 – 5x 5. f(x) =
ax + b
1
Square–root Functions:
1. f(x) = (x – 3)1/2 2. f(x) = (3x – 2)1/2
4. f(x) =(3x – 2)–1/2 5. f(x) = √ax + b
The Algebra of Difference Quotient
3. f(x) = (x – 3)–1/2