The document discusses various methods for generating continuous random variables in simulations, including the inverse transform method and acceptance-rejection method. It provides examples of how to generate random variables from important distributions like the exponential, normal, Poisson, and nonhomogeneous Poisson distributions. The agenda includes an introduction, overview of methods, generating specific distributions, summary, and exercises in R to apply the methods.

1. Chair of Information Systems IV (ERIS)
Institute for Enterprise Systems (InES)
16 April 2013, 10.15 am – 11.15 am
Martin Kretzer
Phone: +49 621 181 3276
E-Mail: kretzer@es.uni-mannheim.de
Generating Continuous Random Variables
(IS 802 “Simulation”, Section 3)

2. Agenda 2
Agenda
1 Introduction
2 Selected Methods
3 Generating Important Distributions
4 Summary
5 Exercises (Simulations using R)
Generating Continuous Random Variables

3. Why “Generation of Continuous Random Variables”? 3
 Simulations are able to address magnifold questions, e.g.:
 How many customers will we have?
 How long does it take to handle arriving customers?
 Will queues develop?
 Problem: Simulations require random variables
 Uniformly distributed random variables are often not enough, but can be used for generation of further distributions
 Uniformly distributed random variables can be generated, e.g., modulo function (section 2)
 Example: Customers in a store arrive randomly, between 10 and 20 minutes apart, normally / exponentially
distributed on this interval.
 Goal: Generate random variables
 Discrete random variables (section 2)
 Continuous random variables (univariate) (section 3)
 Each method for generating a discrete random variable has its analogue in the continuous case!
 Multivariate normal distributed variables (section 4)
Generating Continuous Random Variables
Discrete Variables Continuous Variables
 Finite set of values
 Example: population
 0, 1, 2, 3, …

4. Learning Outcomes 4
Generating Continuous Random Variables
 Generate random variables using the
Inverse-Transform and Acceptance-Rejection
Method
 Develop algorithms for simulating
Exponential, Normal, Poisson and
Nonhomogeneous Poisson distributions
 Perform simulations using R

5. Agenda 5
Agenda
1 Introduction
2 Selected Methods
2.1 Inverse Transform Method
2.2 Acceptance Rejection Method
3 Generating Important Distributions
4 Summary
5 Exercises (Simulations using R)
Generating Continuous Random Variables

6. 
Inverse Transform Method: Proof 6
Generating Continuous Random Variables

7. Inverse Transform Method: Example 7

Generating Continuous Random Variables
3
xxF
31
uuF
3n

8. Acceptance-Rejection Method 8

Generating Continuous Random Variables

9. Acceptance-Rejection Method: Example 9

Generating Continuous Random Variables
3
120 xxxf

10. Agenda 10
Agenda
1 Introduction
2 Selected Methods
3 Generating Important Distributions
3.1 Exponential Distribution
3.2 Normal Distribution
3.3 Poisson Distribution
3.4 Nonhomogeneous Poisson Distribution
4 Summary
5 Exercises (Simulations using R)
Generating Continuous Random Variables

11. Exponential Distribution (1/2) 11

Generating Continuous Random Variables

12. Exponential Distribution (2/2) 12
Generating Continuous Random Variables
x
exF
uuF ln
1
11

13. Normal Distribution (1/4) 13
Generating Continuous Random Variables


14. Normal Distribution (2/4) 14
Generating Continuous Random Variables

5.0;
5.0;
*
22
22
UY
UY
Xi

15. 5.0;
5.0;
*
1
1
UY
UY
Xi
Normal Distribution (3/4) 15
Generating Continuous Random Variables


16. Normal Distribution (4/4) 16
 Graphical illustration
Generating Continuous Random Variables
)(
)(
xg
xf
xh
2
2
2
2
x
exf
x
exg

17. 
Poisson Process 17
Generating Continuous Random Variables

18. Comparison: Homogeneous and Nonhomogeneous Poisson Process 18
Generating Continuous Random Variables
Nonhomogeneous Poisson Process(Homogeneous) Poisson Process
Previously: Now:

19. Nonhomogeneous Poisson Process (1/2) 19

Generating Continuous Random Variables
simulation of a
Poisson process
randomly
counting events

20. Nonhomogeneous Poisson Process (2/2) 20

Generating Continuous Random Variables

21. Agenda 21
Agenda
1 Introduction
2 Selected Methods
3 Generating Important Distributions
4 Summary
5 Exercises (Simulations using R)
Generating Continuous Random Variables

22. 
Summary 22
Generating Continuous Random Variables
Distribution
Inverse Transform
Method
Acceptance-Rejection
Method
Exponential X
Normal X
(Homogeneous)
Poisson
X
Nonhomogeneous
Poisson
X

23. Agenda 23
Agenda
1 Introduction
2 Selected Methods
3 Generating Important Distributions
4 Summary
5 Exercises (Simulations using R)
5.1 Exercise 1 – Inverse Transform Method (Exponential Distr.)
5.2 Exercise 2 – Acceptance Rejection Method (Normal Distr.)
Generating Continuous Random Variables

24. Exercise 1 – Task 24

Generating Continuous Random Variables

25. Exercise 1 – Live Demonstration 25
 R
 Version: 3.0.0 (Windows 32-bit)
 http://cran.rstudio.com/
 RStudio
 Version: 0.97.336
 http://www.rstudio.com/ide/download/
Generating Continuous Random Variables

26. Exercise 1 – Code 26
####################################
### Author: Martin Kretzer
### Date: 11 April 2012
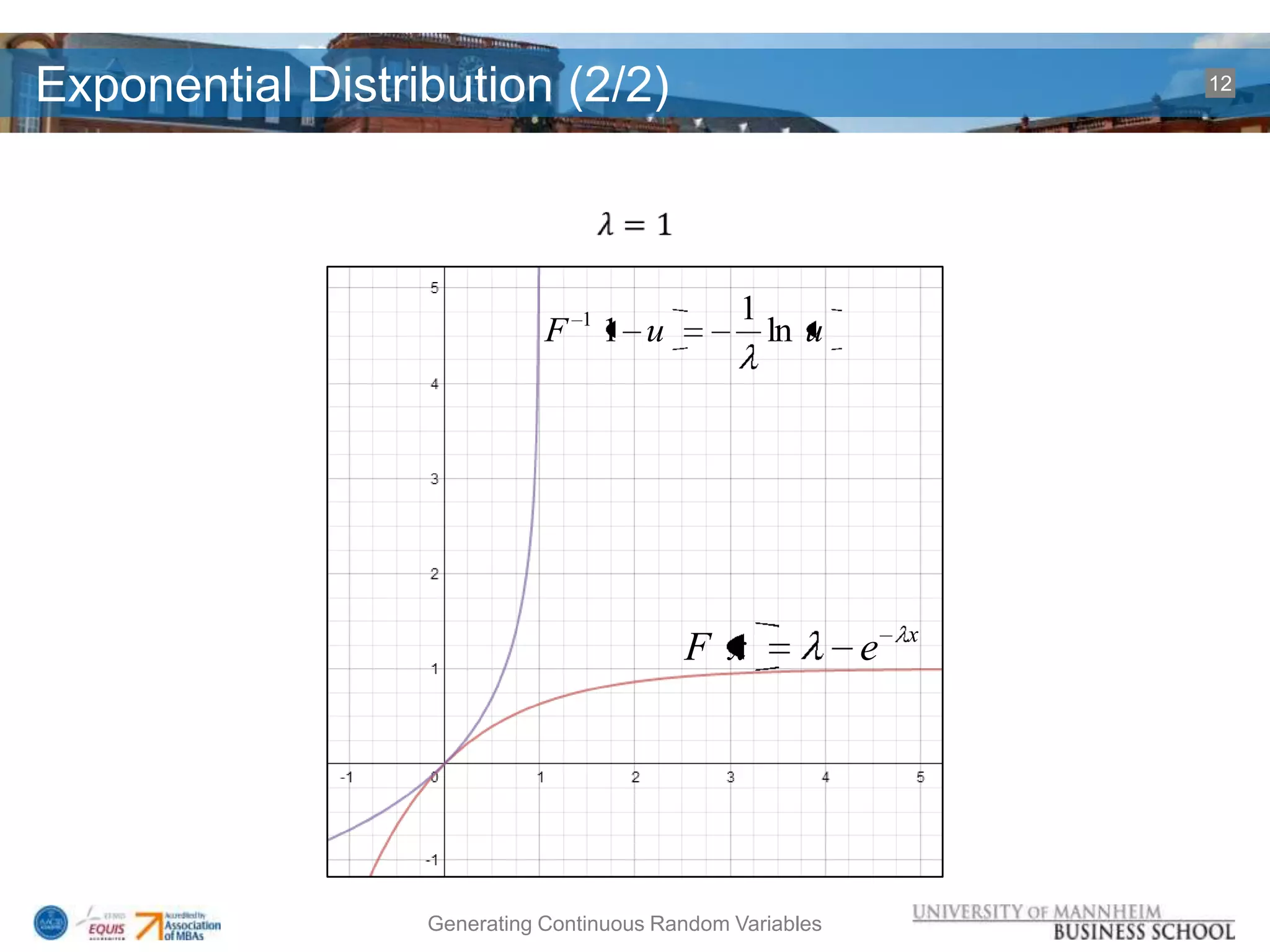
### Descr: Simulation of an exponential distribution + inverse transform method
####################################
### 0. Functions:
### Performs simulations and returns a list of all resulting values
getSimulationsVector<- function( numberOfSimulations, numberOfCustomers, mean,
probability )
{
lambda<- 1/mean
simulationsVector<- c()
for( i in 1:numberOfSimulations )
{
claimsPerSimulationVector<- c()
#uniformVars<- runif( numberOfCustomers )
for( j in 1:numberOfCustomers )
{
uniformVarProbability <- runif(1)
if( uniformVarProbability <= probability )
{
uniformVarAlgorithm <- runif(1)
claim<- -(1/lambda)*log( uniformVarAlgorithm )
claimsPerSimulationVector<- c( claimsPerSimulationVector, claim )
}
}
simulationsVector<- c(simulationsVector, sum(claimsPerSimulationVector) )
}
return(simulationsVector)
};
Generating Continuous Random Variables
### Probability that all values are above the variable limit
getProbability<- function( simulationsVector, limit )
{
eventcount<- 0
for( i in 1:length( simulationsVector ) )
{
if( simulationsVector[[i]] >= limit )
{
eventcount<- eventcount + 1
}
}
probability<- eventcount / length( simulationsVector )
return(probability)
};
####################################
### 1. Set constant variables:
numberOfSimulations<- 100000;
numberOfCustomers<- 1000
mean<- 800;
limit<- 50000;
probability<- 0.05;
### 2. Execute and output variables:
simulationsVector <- getSimulationsVector( numberOfSimulations,
numberOfCustomers, mean, probability );
simulationsVector; #R maximum outputs 10000 values
### 3. Execute and output variables:
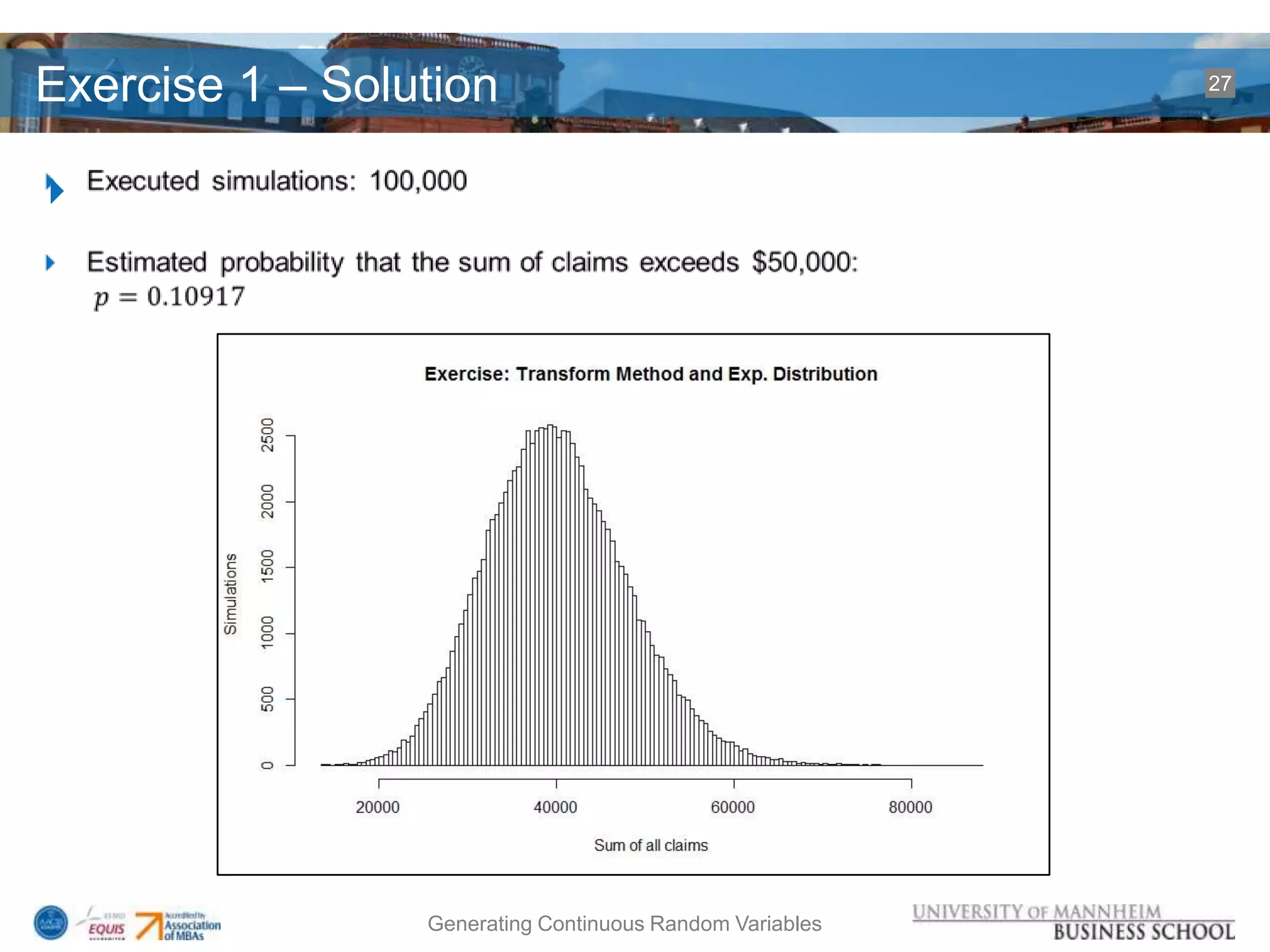
hist(simulationsVector, 250, xlab="Sum of all
claims",ylab="Simulations",main="Exercise: Transform Method and Exp.
Distribution");
### 4. Calculate and output probability:
probability<- getProbability( simulationsVector, limit );
probability;

27. Exercise 1 – Solution 27

Generating Continuous Random Variables

28. 5.0;
5.0;
*
1
1
UY
UY
Xi
Exercise 2 – Task 28

Generating Continuous Random Variables

29. Exercise 2 – Live Demonstration 29
 R
 Version: 3.0.0 (Windows 32-bit)
 http://cran.rstudio.com/
 RStudio
 Version: 0.97.336
 http://www.rstudio.com/ide/download/
Generating Continuous Random Variables

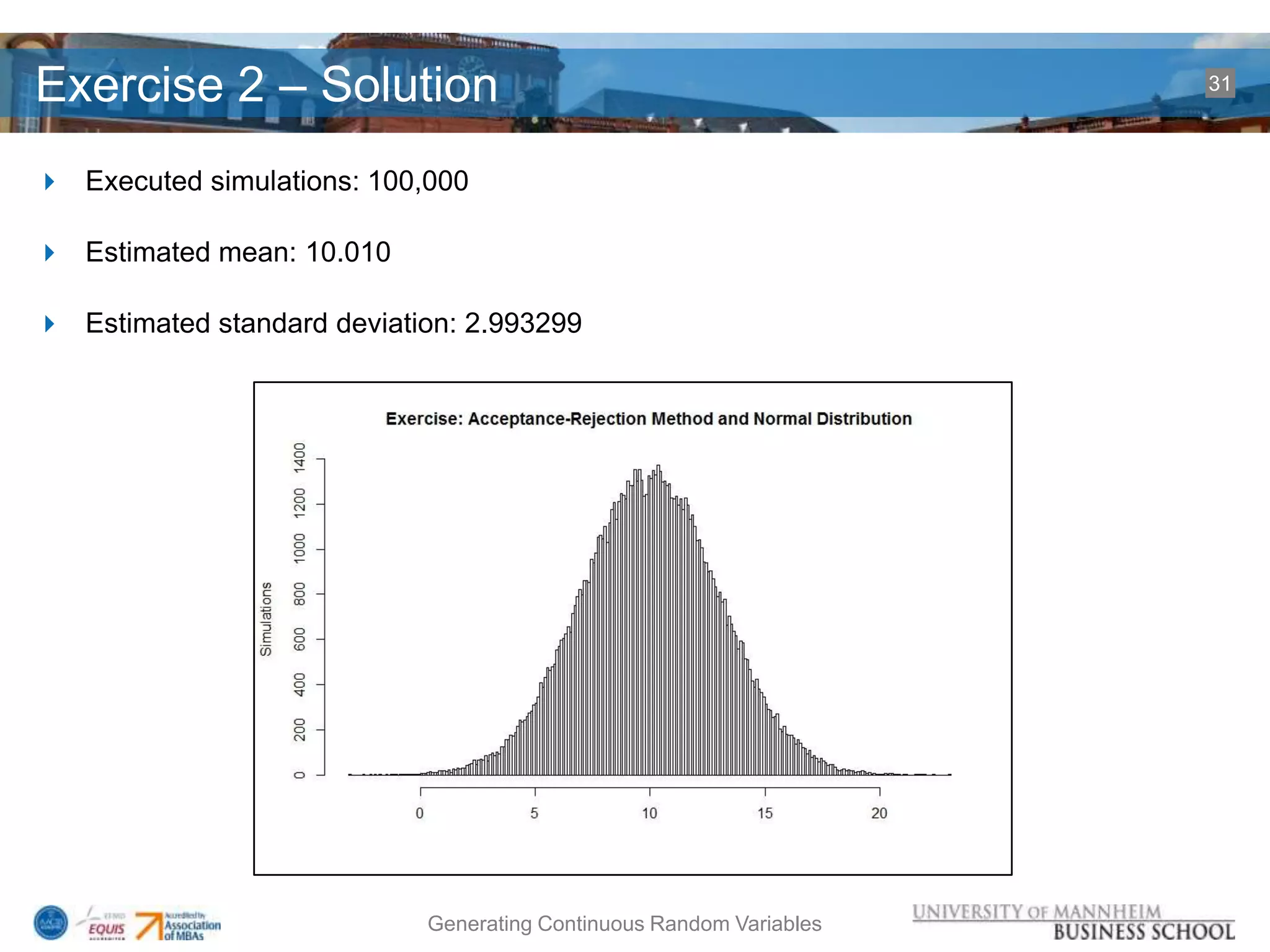
30. Exercise 2 – Code 30
####################################
### Author: Martin Kretzer
### Date: 12 April 2012
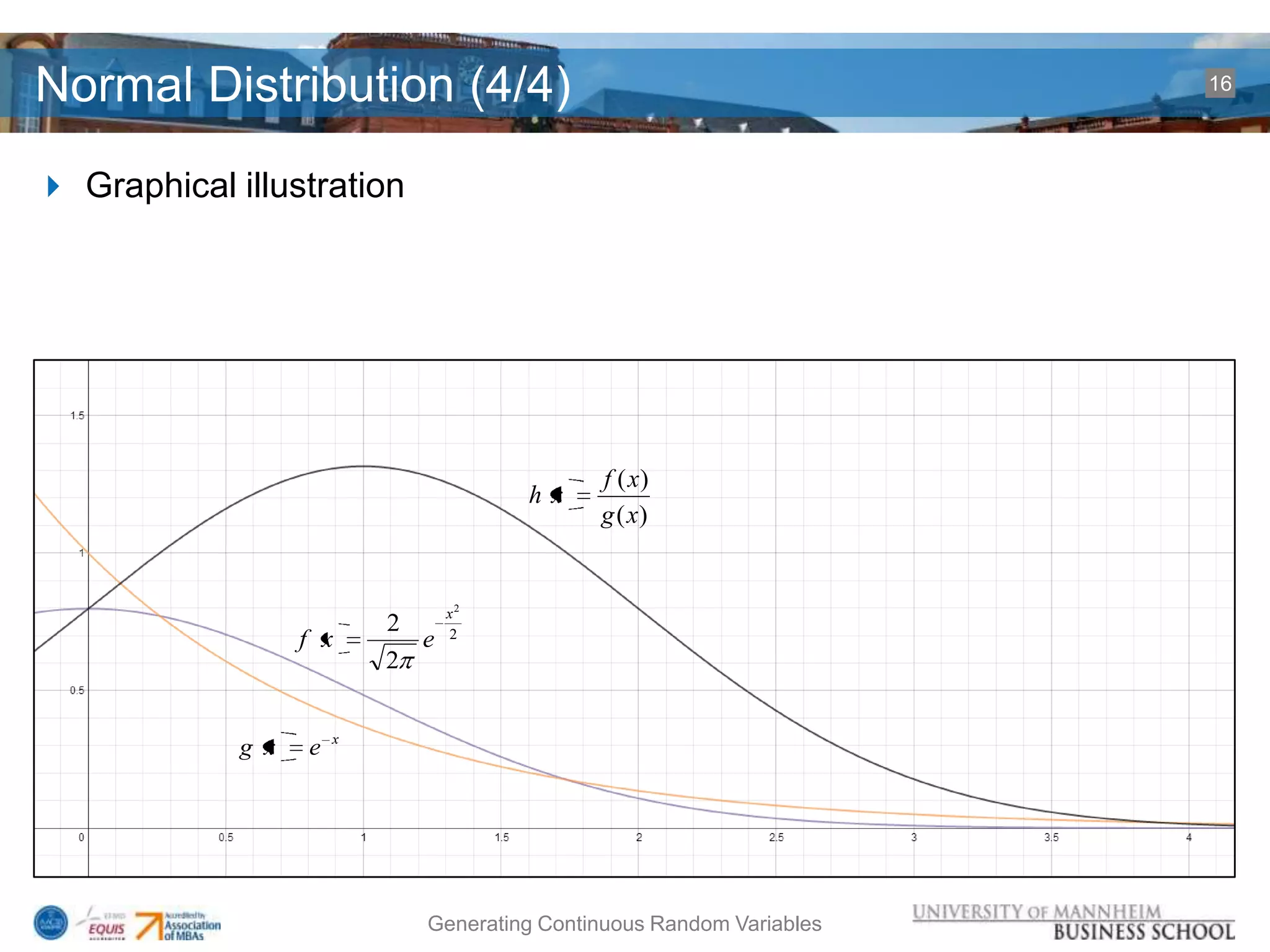
### Descr: Simulation of a half-normal distribution + accept/reject
####################################
### 0. Function:
### Performs simulations and returns a vector of all simulated values
getSimulationsVector<- function( numberOfSimulations, mean, stdDev )
{
# Define variables
simulations.vector<- rep(0, numberOfSimulations)
# Generate the exponential variable y1
y1<- runif(1)
y1<- -log(y1)
for( i in 1:numberOfSimulations )
{
# Generate the independent exp. variable y2
y2<- runif(1)
y2<- -log(y2)
# Acceptance-Rejection procedure
while( y2 < (y1-1)^2/2 )
{
# if rejected, generate two new independent exp. variables y1 and
# y2 and repeat procedure
y1<- runif(1)
y1<- -log(y1)
y2<- runif(1)
y2<- -log(y2)
}
Generating Continuous Random Variables
y3<- y2-(y1-1)^2/2
# Generate a random number U and store the simulated variable y1
# in simulations.vector
u<- runif(1)
if( u <= 0.5 )
{
simulations.vector[i]<- mean + (y1*stdDev)
}
else
{
simulations.vector[i]<- mean + (-y1*stdDev)
}
y1<- y3
}
return(simulations.vector)
};
####################################
### Function End
####################################
simulations.vector<- getSimulationsVector( 100000, 10, 3 )
summary( simulations.vector )
sd( simulations.vector )
hist(simulations.vector, 250,
xlab="",ylab="Simulations",main="Exercise: Acceptance-Rejection Method
and Normal Distribution");

31. Exercise 2 – Solution 31
 Executed simulations: 100,000
 Estimated mean: 10.010
 Estimated standard deviation: 2.993299
Generating Continuous Random Variables

32.  Thank you for your attention.
32
Generating Continuous Random Variables

33. Appendix 33
Appendix
1 Backup Slides
2 Bibliography
Generating Continuous Random Variables

34. Poisson Process Introduction (1/2) 34

Generating Continuous Random Variables

35. Poisson Process Introduction (2/2) 35

Generating Continuous Random Variables

36. Nonhomogeneous Poisson Process: Option 1 Improvement 36

Generating Continuous Random Variables

37. Nonhomogeneous Poisson Process: Option 2 37

Generating Continuous Random Variables

38. Appendix 38
Appendix
1 Backup Slides
2 Bibliography
Generating Continuous Random Variables

39. Bibliography 39
 ETH Zürich. 2013. The Uniform Distribution, ETH Zürich, Zürich, CH (available online at
http://stat.ethz.ch/R-manual/R-devel/library/stats/html/Uniform.html ).
 Haugh, M. 2010. “Generating Random Variables and Stochastic Processes,” Columbia
University, US (available online at http://www.columbia.edu/~mh2078/MCS_ Generate_
RVars .pdf ).
 The R Core Team 2013. “R: A Language and Environment for Statistical Computing.
Reference Index. Version 3.0.0 (2013-04-03),” (part of the R download).
 R-Project 2013. “Probability Distributions,” (available online at http://cran.r-
project.org/web/views/Distributions.html ).
 Ross, S. M. 2013. Simulation, 5th ed., San Diego, CA: Academic Press.
 Sigman, K. 2009. “Inverse Transform Method,” Columbia University, US (available online at
http://www.columbia.edu/~ks20/4404-13-Spring/4404-Notes-ITM.pdf ).
 Valdez, E. A. 2008. “Generating Continuous Random Variables,” University of Connecticut,
US (available at http://www.math.uconn.edu/~valdez/math276s08/Math276-Week45.pdf ).
 Venables, W. N., Smith, D. M., and the R Core Team. 2013. “An Introduction to R. Notes on
R: A Programming Environment for Data Analysis and Graphics Version 3.0.0 (2013-04-
03),” (part of the R download).
Generating Continuous Random Variables