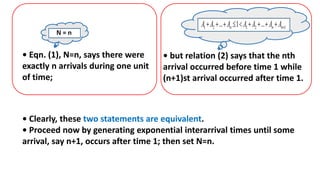
This document contains information about the acceptance-rejection method for generating random variates from a given distribution. It provides an example of how to generate Poisson random variables with a given mean using the acceptance-rejection technique. The technique involves generating random numbers and either accepting or rejecting them based on whether they satisfy certain conditions. If rejected, another random number is generated until one is accepted. The document shows the step-by-step workings of this technique to generate 3 Poisson variates from a sequence of random numbers.

1. Name : Umma Hafsah Himu
Student ID : 1612524130
Topic : Concept of Bayesian
Approach
Group 4
Topic 10: Acceptance - rejection method

2. Name : Md. Emran Hossain
Roll : 1710824166
1
2
3
4
6
5
7
Name : Umma Hafsah Himu
Roll : 1612524130
Name : Al Helal Muhammad Swadhin
Roll : 1710624158
Name : Afsana Afruz Suchi
Roll : 1712524190
Name : Apu Chakraborty
Roll : 1711024180
Name : Saud Anwar Shawon
Roll : 1610424174
Name : Shohel Rana
Roll : 1710824135

3. • There are usually several alternative techniques that can be used for
generating random variates from a given distribution.
• Usually used when inverse transform is not directly applicable or is
inefficient (e.g., gamma, beta)
• The important techniques (methods) are:
1. Inverse transform technique
2. Composition technique
3. Convolution technique
4. Acceptance-rejection technique
Techniques for generating random variate

4. • In this technique, random variates with a distribution are
generated until some condition are satisfied.
• When the condition is finally satisfied, the desired random
variate can be computed.
Acceptance-Rejection technique

5. For example:
Suppose that an analyst needed to devise a method for
generating random variates, X, uniformly distributed
between ¼ and 1.

6. Step 1:
Generate a random number R.
Step 2a:
If R ≥ ¼, accept X=R, then go to step 3.
Step 2b:
If R < ¼, reject R, and return to step 1.
Step 3:
If another uniform random variate on [1/4, 1] is needed,
repeat the procedure beginning at step 1. If not stop.
One way to proceedwouldbe to followthese steps:
Step 2a is an “acceptance” and step 2b is a “rejection” in this
acceptance-rejection technique.

7. • A Poisson random variable, N, with mean α > 0 can be expressed as
• N can be interpreted as the number of arrivals from a Poisson arrival
process in one unit of time.
• But the interarrival times, A1, A2, … of successive customers are
exponentially distributed with rate α (i.e., α is the mean number of
arrivals per unit time).
Poisson distribution:
Example:
n = 0,1,…

8. • Thus there is a relationship between the (discrete) Poisson
distribution and the (continuous) exponential distribution,
namely:
N = n ---------------- (1)
• if and only if
---------------- (2)

9. • Clearly, these two statements are equivalent.
• Proceed now by generating exponential interarrival times until some
arrival, say n+1, occurs after time 1; then set N=n.
• Eqn. (1), N=n, says there were
exactly n arrivals during one unit
of time;
• but relation (2) says that the nth
arrival occurred before time 1 while
(n+1)st arrival occurred after time 1.

10. • For efficient generation purposes, relation (2) is usually simplified by
first using the exponential generating equation, 𝑨𝒊 = −
𝟏
α
𝐥𝐧 𝑹𝒊 , to
obtain
• Next multiply through by –α, which reverses the sign of the
inequality, and use the fact that a sum of logarithms is the logarithm
of a product, to get

11. • Finally, use the relation 𝒆𝒍𝒏 𝒙
= x for any number x to obtain
• which is equivalent to relation (2).
---------------- (3)

12. Step 1:
Set n=0, P=1
Step 2:
Generate a random number 𝑹 𝒏+𝟏 and replace P by P. 𝑹 𝒏+𝟏
Step 3:
If P < 𝒆−α, then accept N=n.
Otherwise, reject the current n, increase n by 1, and return to step 2.
The procedure for generating a Poisson random variate, N, is given
by the following steps:

13. Generate 3 Poisson variates with mean α=0.2. Use the following sequence
of random numbers, R: 0.4357, 0.4146, 0.8353, 0.9952, 0.8004, 0.7945.
Example: Poisson distribution:
Step 1: Set n=0, P=1
Step 2: 𝑹 𝟏=0.4357, P= 1. 𝑹 𝟏 =0.4357
Step 3: Since P=0.4357 < 𝒆−α = 𝒆− 𝟎.𝟐 =0.8187, accept N=0.
Step 1-3: (𝑹 𝟏=0.4146 leads to N=0)
Step 1: Set n=0, P=1
Step 2: 𝑹 𝟏=0.8353, P = 1. 𝑹 𝟏 =0.8353
Step 3: Since P≥ 𝒆−α, reject n=0 and return to step 2 with n=1

14. n R 𝐧+𝟏 P Accept/Reject Result
0 0.4357 0.4357 P < 𝐞−α (accept) N=0
0 0.4146 0.4146 P < 𝐞−α (accept) N=0
0 0.8353 0.8353 P ≥ 𝐞−α (reject)
1 0.9952 0.8313 P ≥ 𝐞−α (reject)
2 0.8004 0.6654 P < 𝐞−α (accept) N=2
Step 2: 𝑹 𝟐 =0.9952, P=𝑹 𝟏. 𝑹 𝟐=0.8313
Step 3: Since P≥ 𝒆−α, reject n=1 and return to step 2 with n=2
Step 2: 𝑹 𝟑=0.8004, P=𝑹 𝟏. 𝑹 𝟐. 𝑹 𝟑=0.6654
Step 3: Since P<𝒆−α , accept N=2.

15. References:
Slides and lectures of Professor Dr. Md. Rezaul Karim,
Department of Statistics, University of Rajshahi.
web.ics.purdue.edu/~hwan/IE680/Lectures/Chap08Slides
.pdf
Law, A. M., & W. Kelton (2000). Simulation modeling and
analysis. Mac Graw Hill, Boston, Burr Ridge, USA.

16. 16