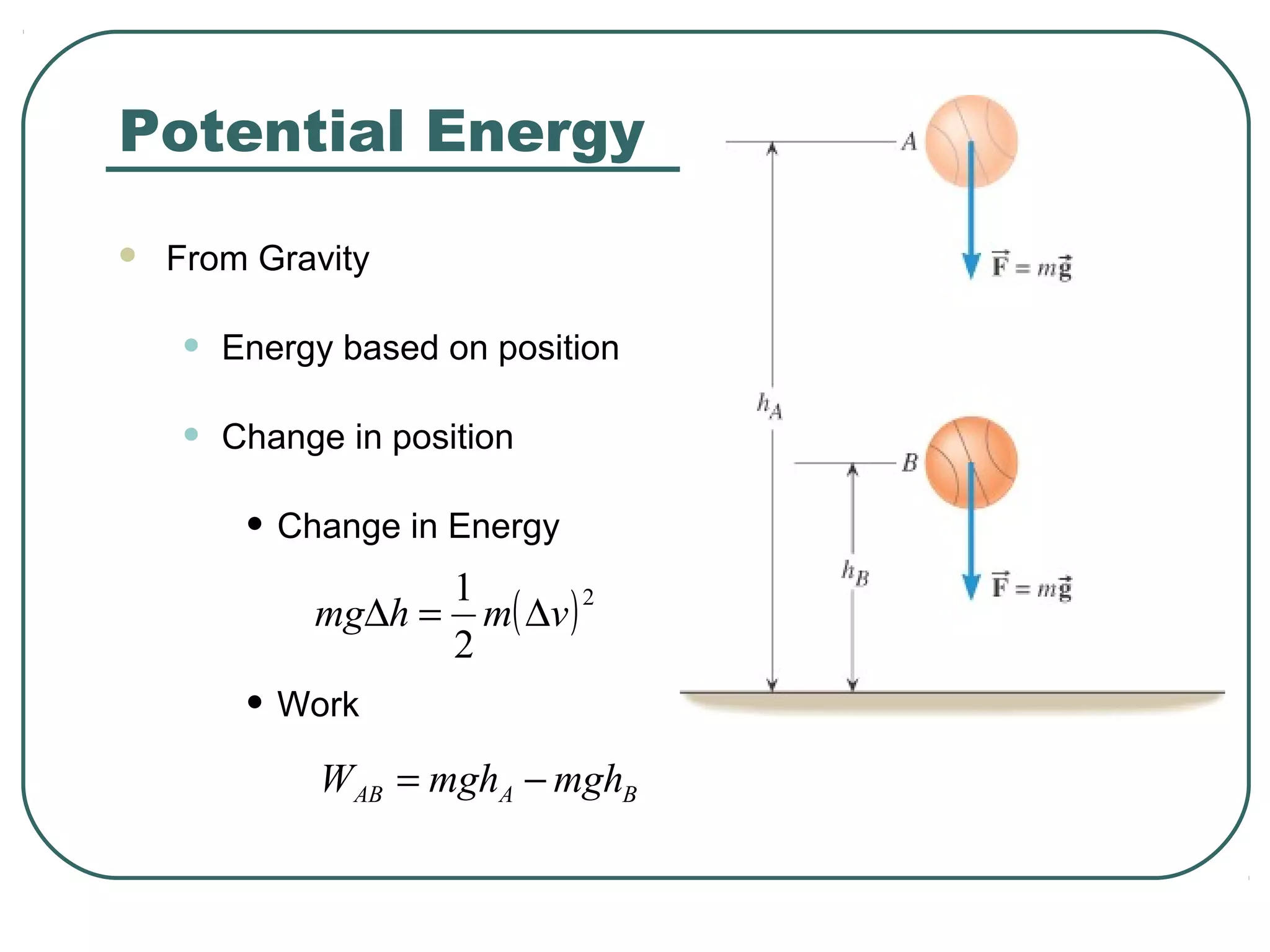
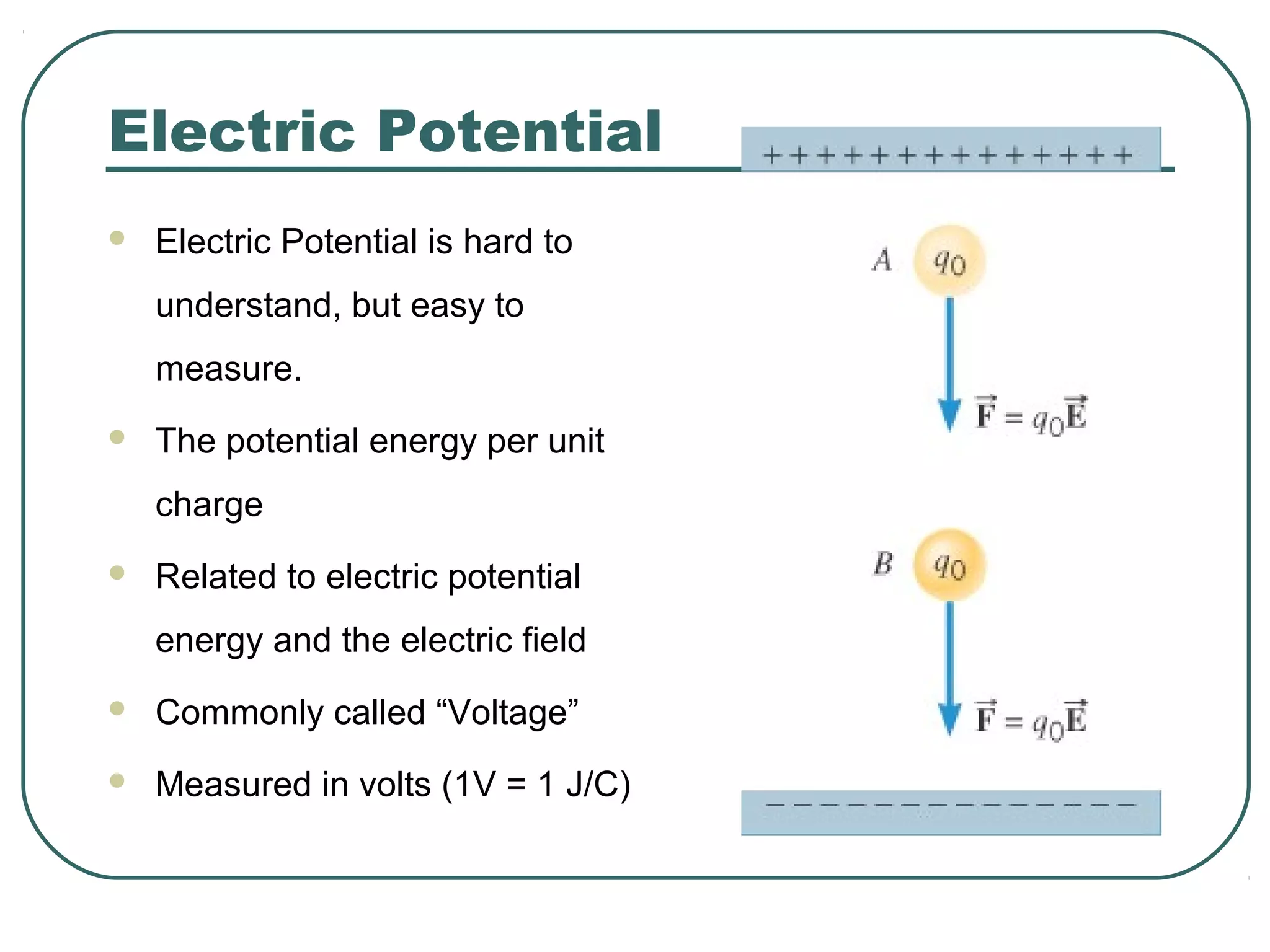
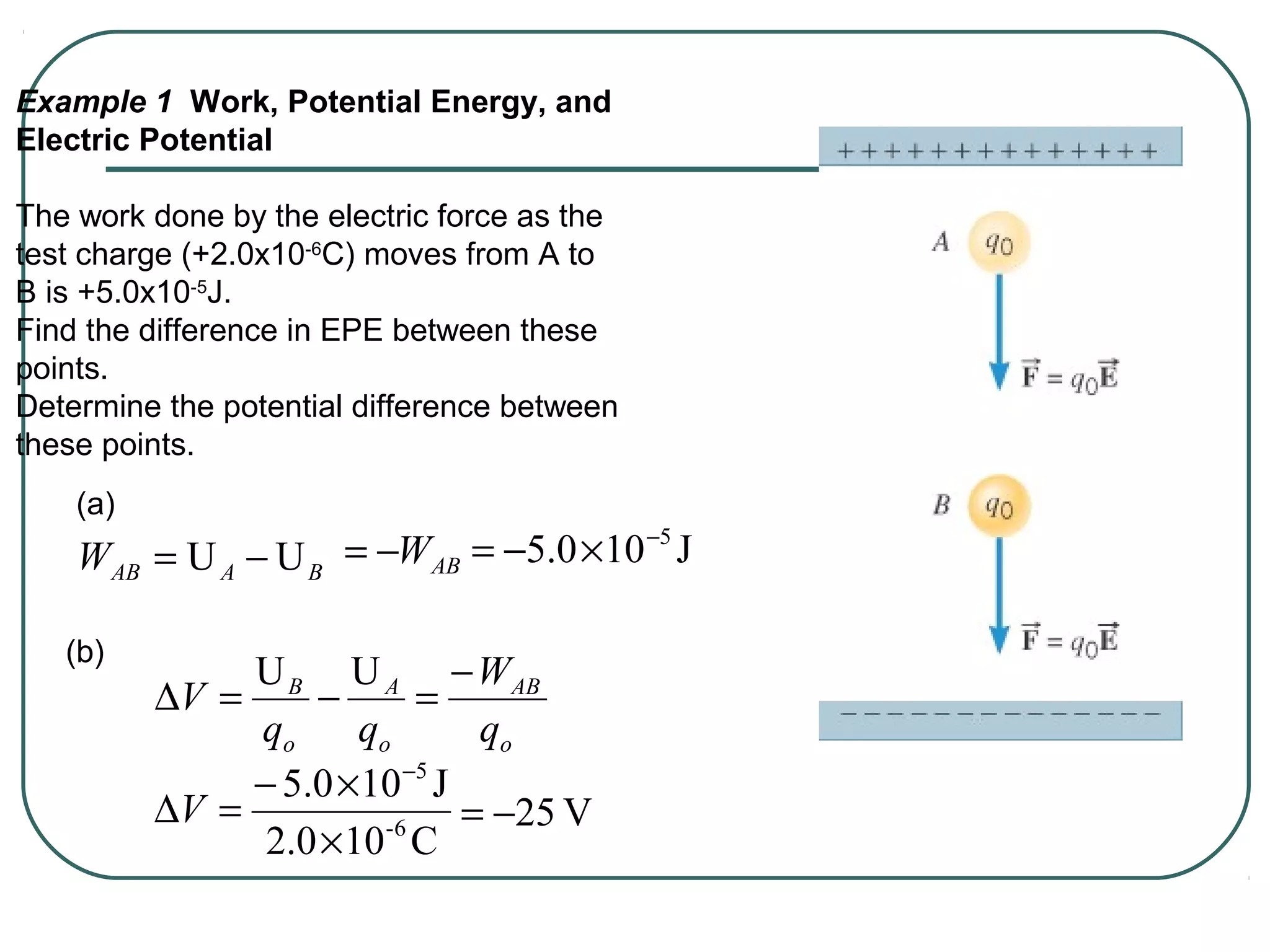
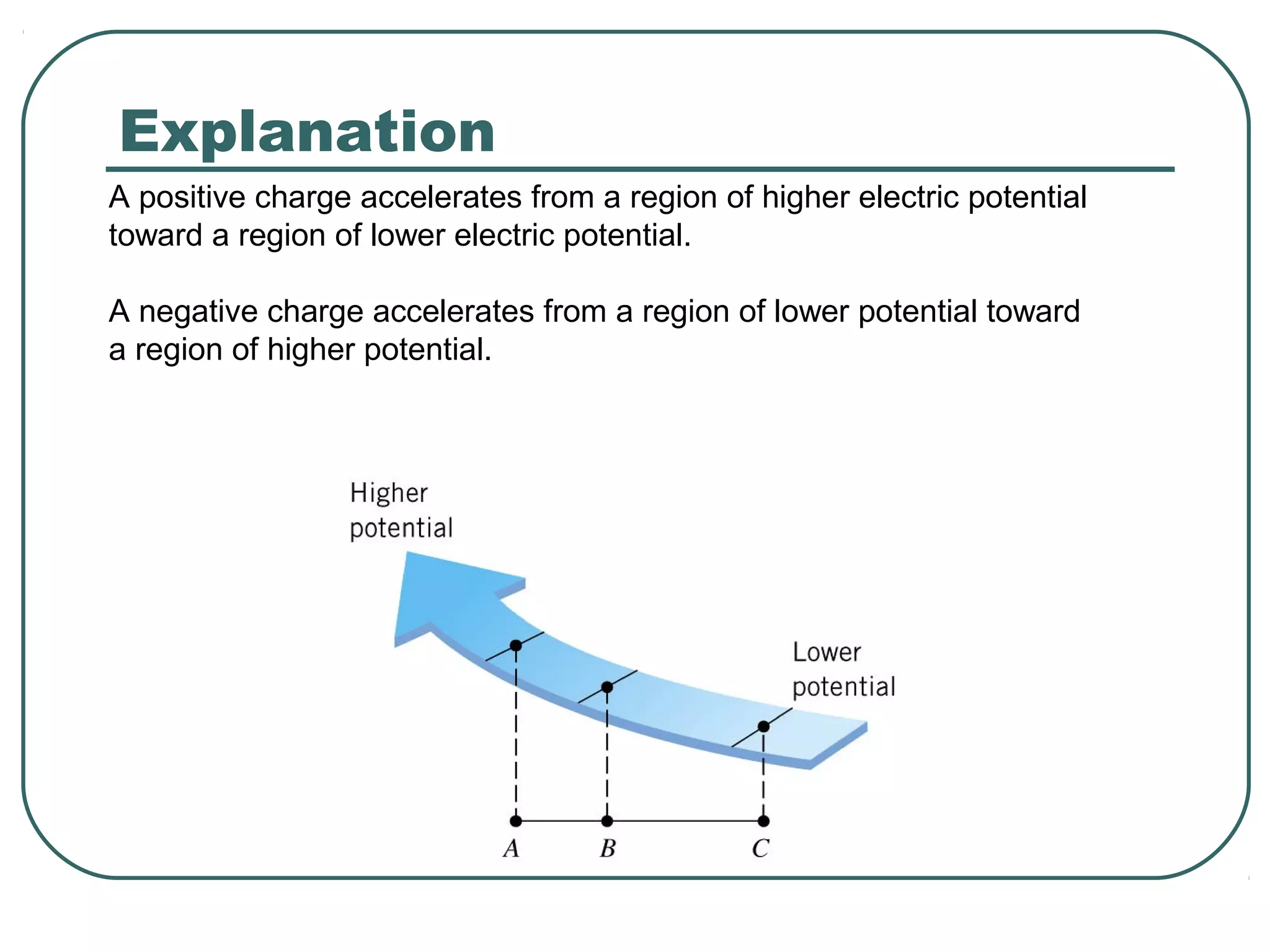
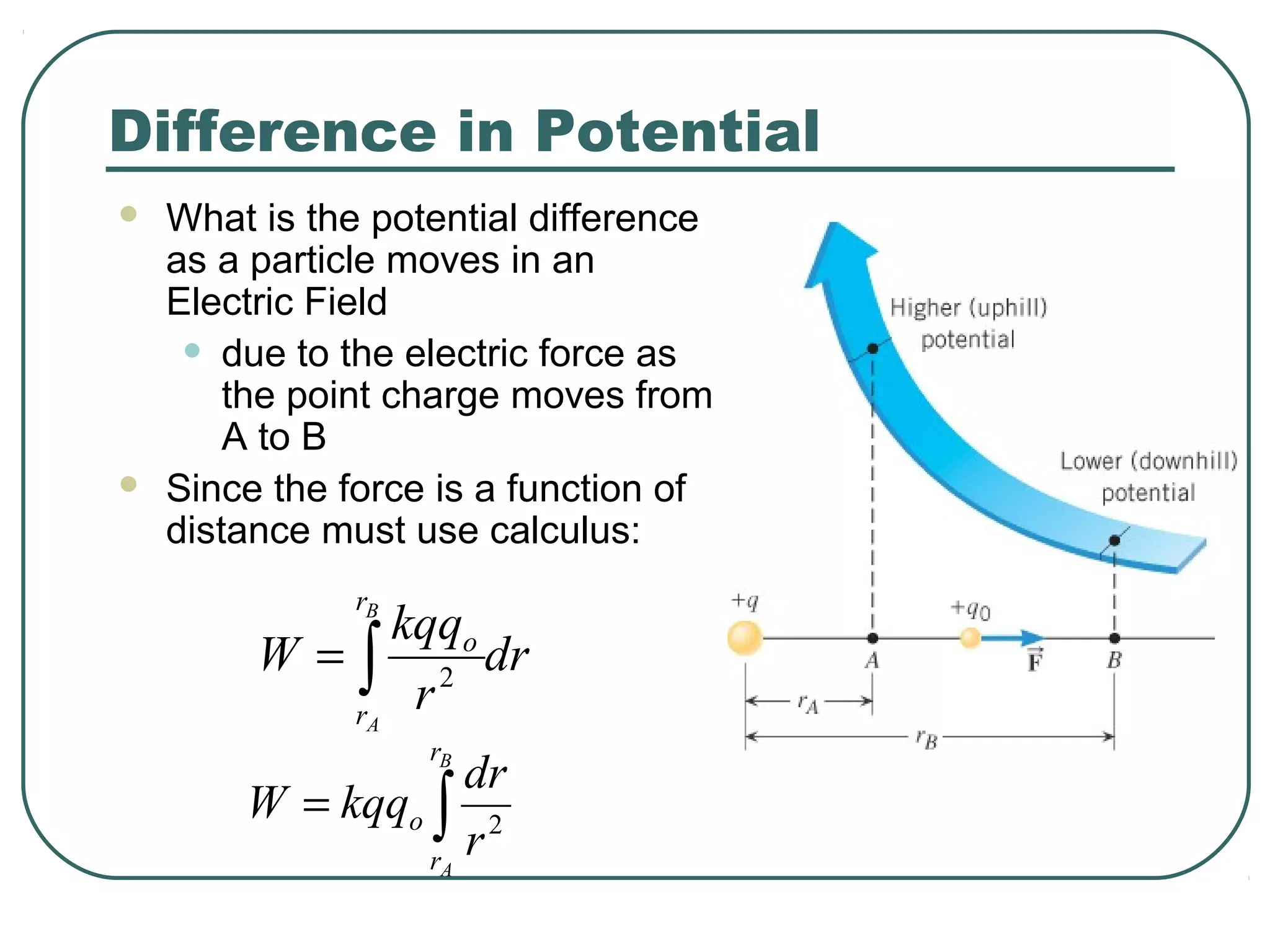
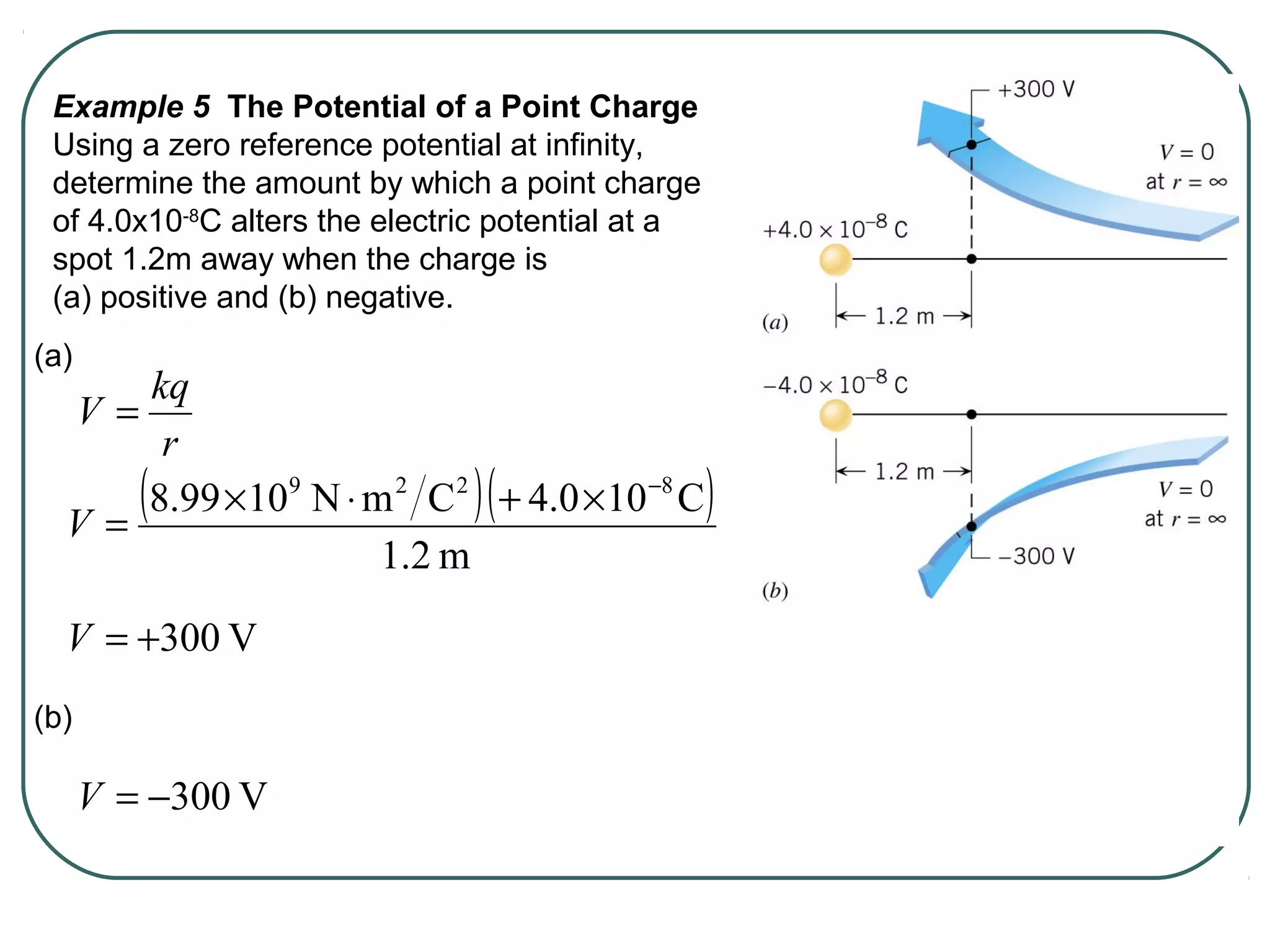
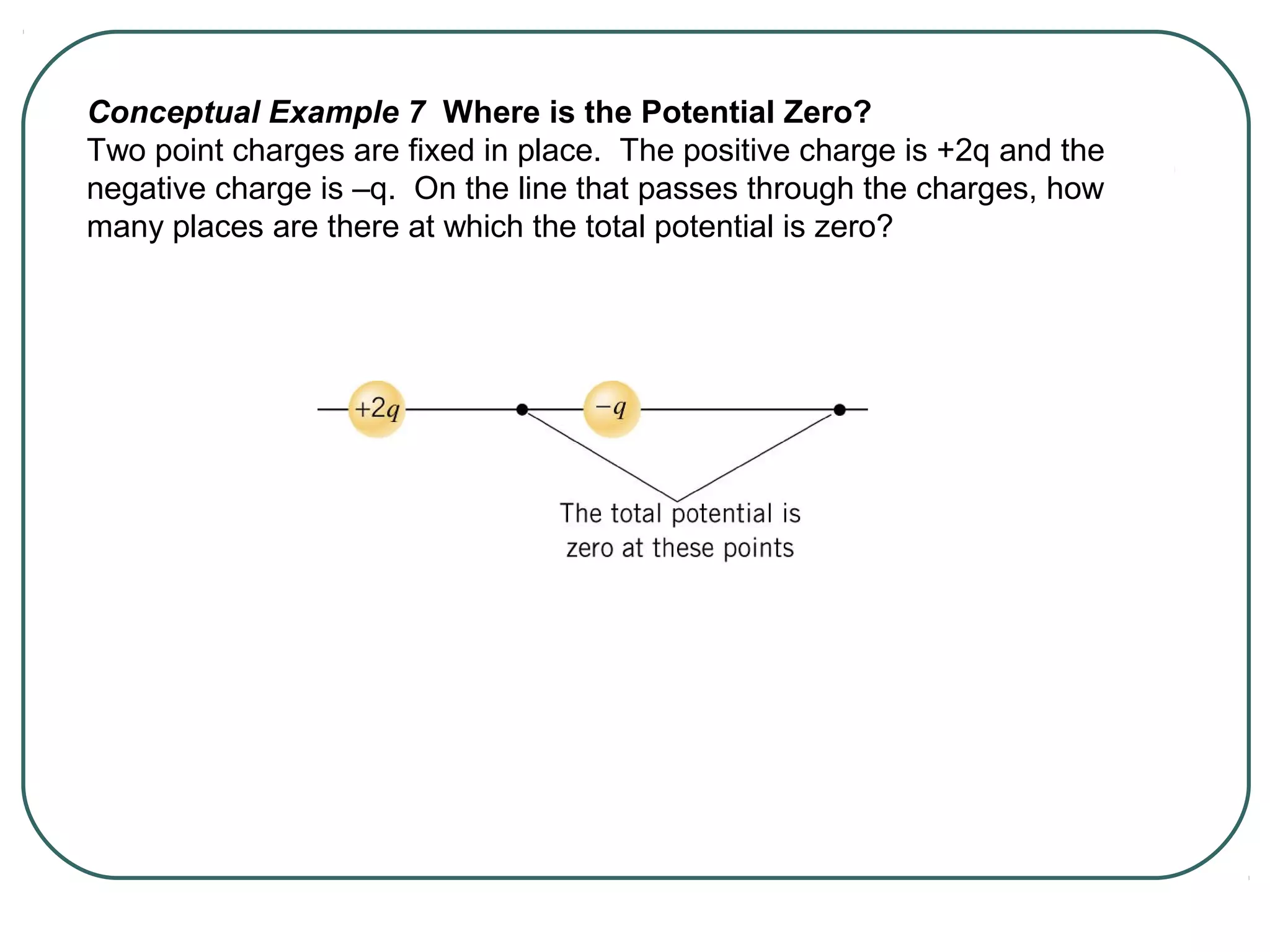
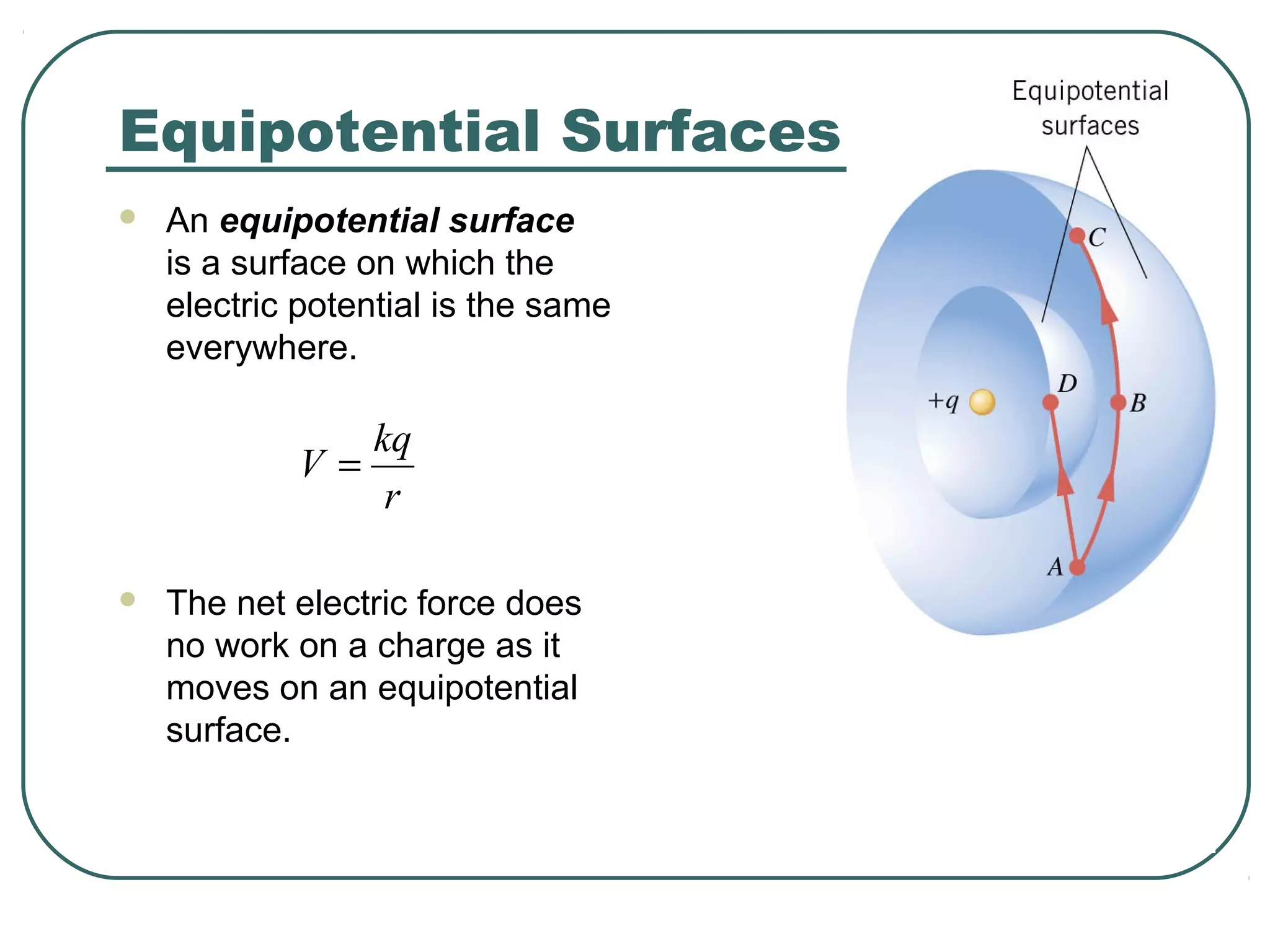
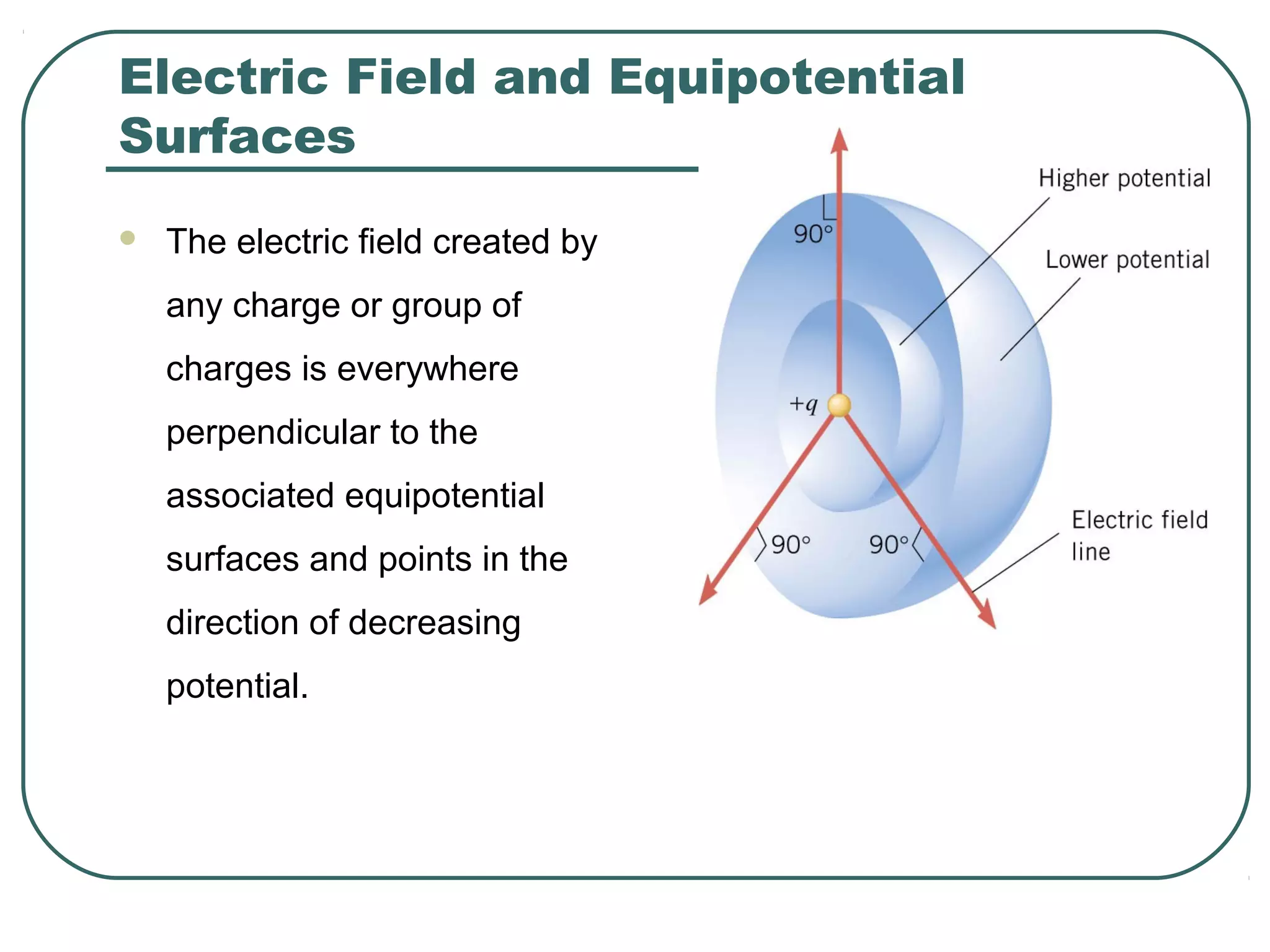
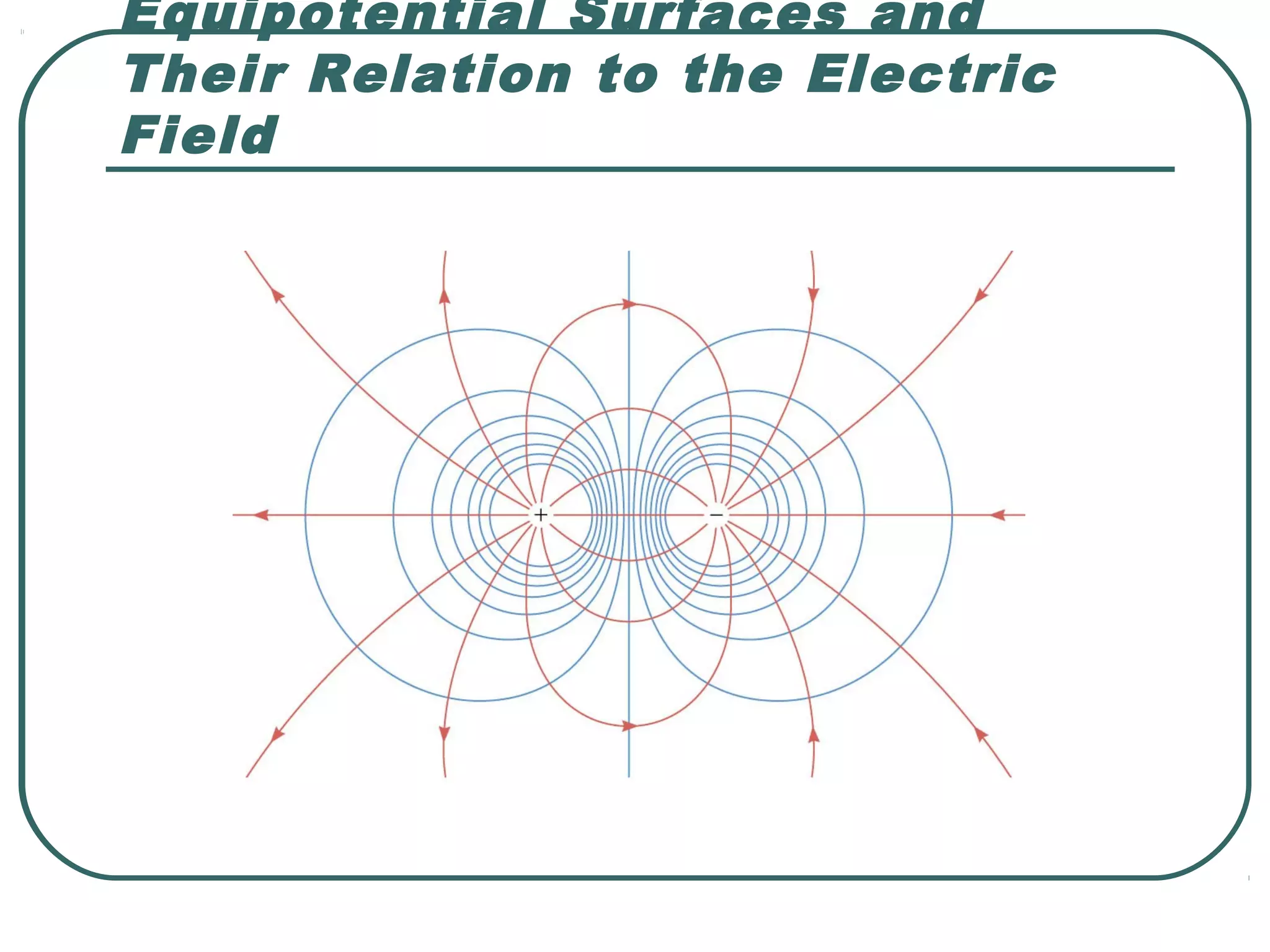
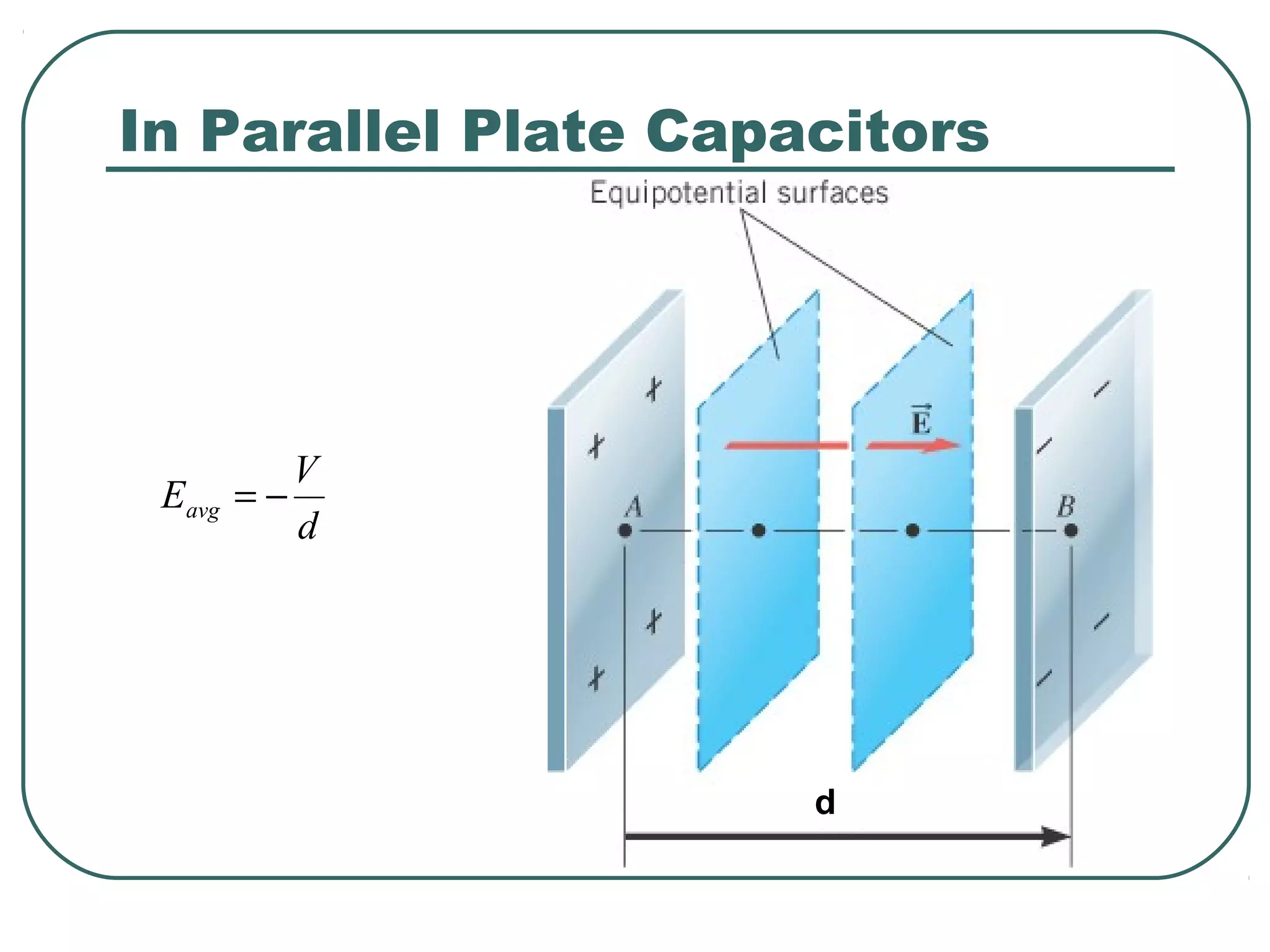
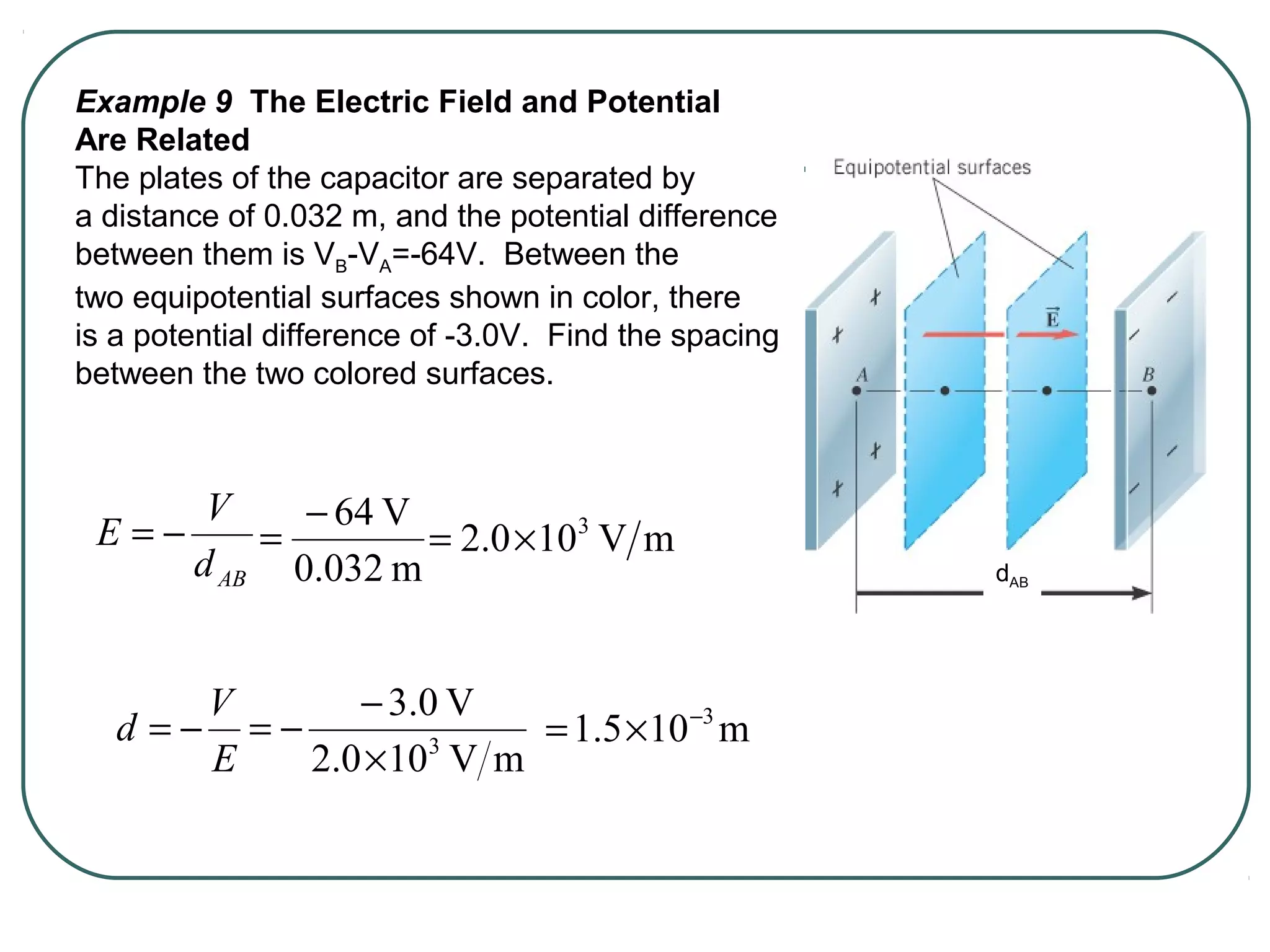
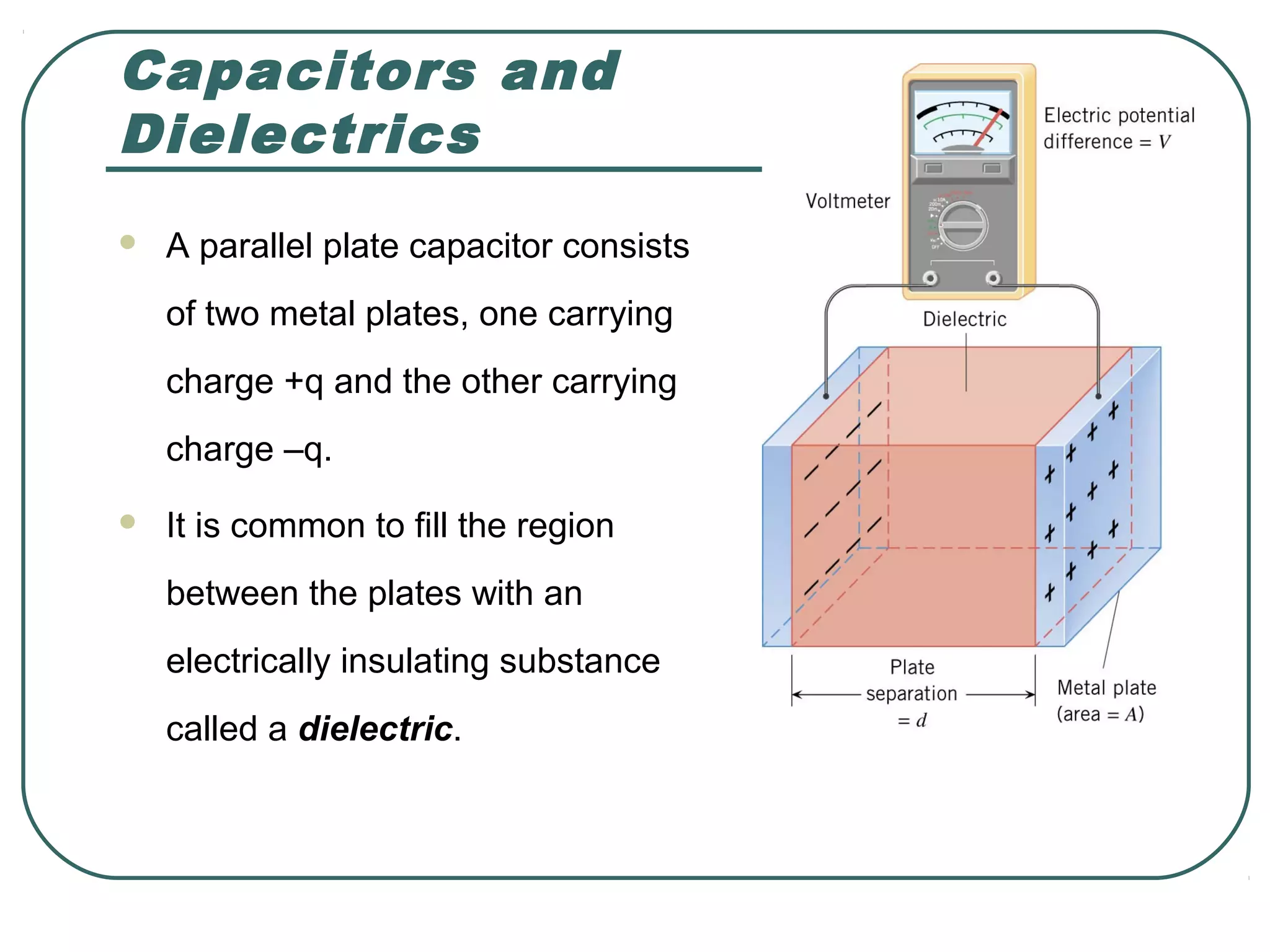
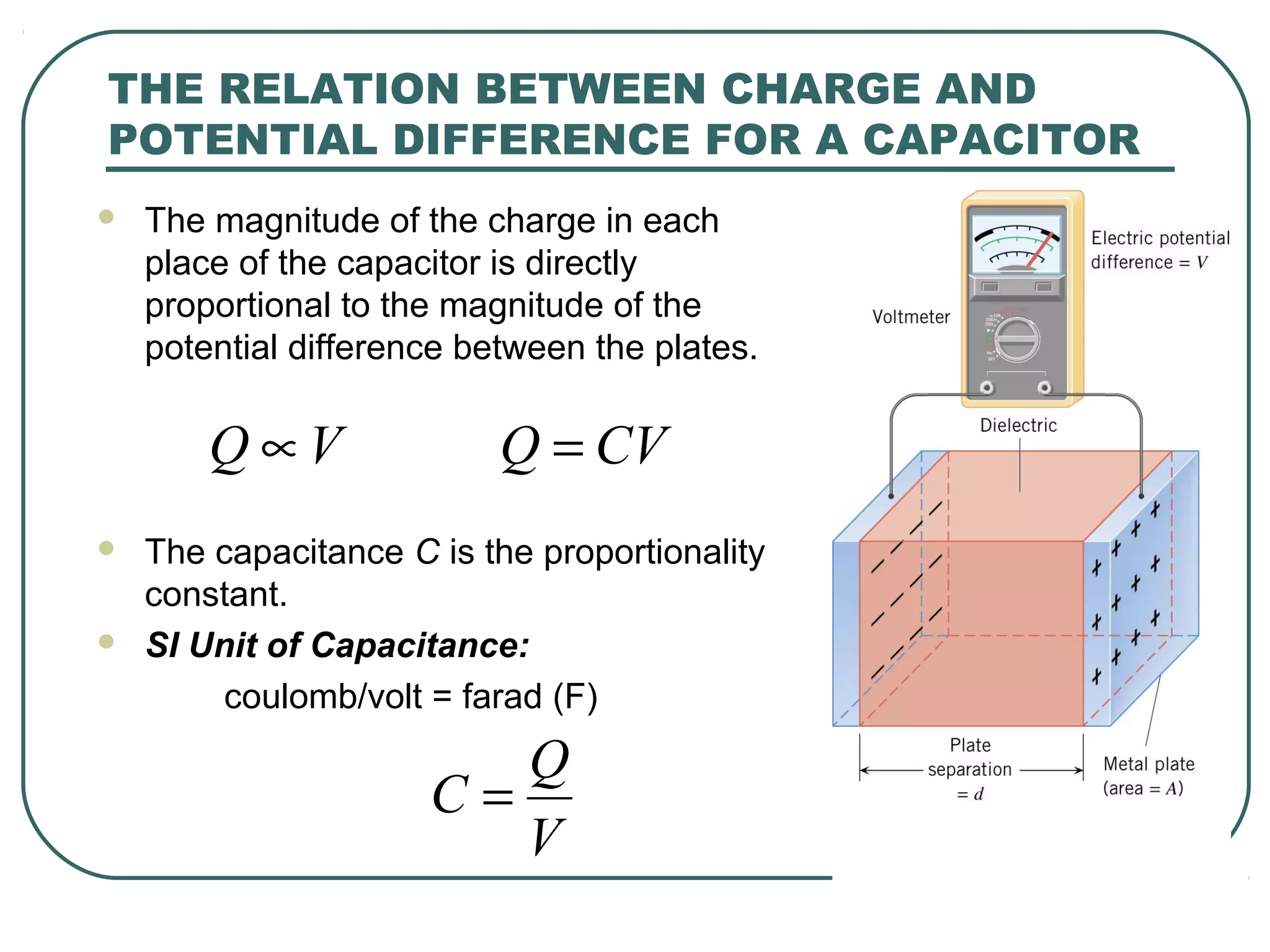
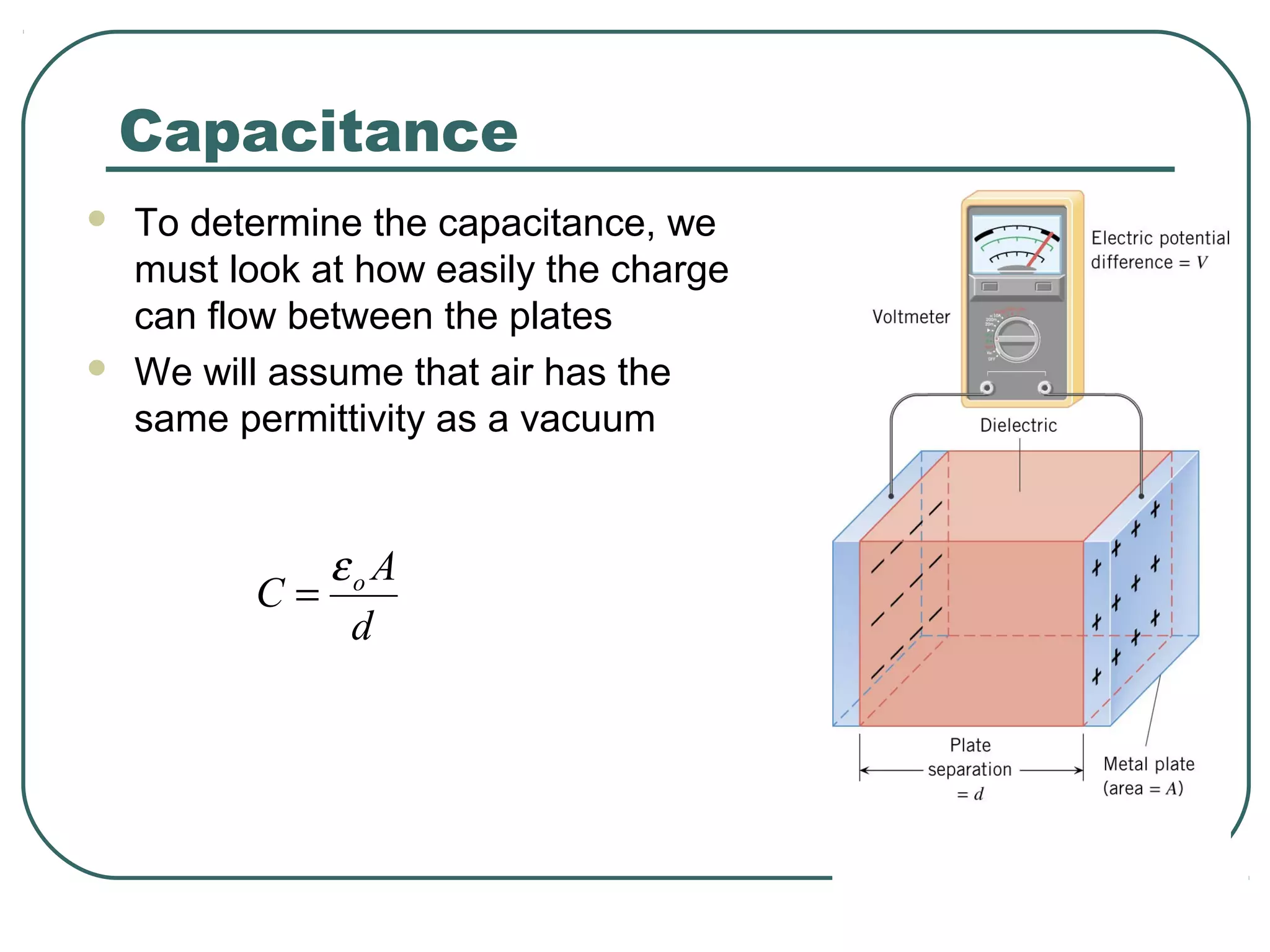
This document provides learning objectives and content about electric potential energy and electric potential. It discusses key concepts such as electric field, electric potential, equipotential surfaces, and capacitors. Specifically, it defines electric potential as electric potential energy per unit charge. It also explains that equipotential surfaces represent positions of equal electric potential and that the electric field is perpendicular to equipotential surfaces. Finally, it introduces capacitors as devices that can store electric potential energy between two conductors, such as the plates of a parallel plate capacitor, and how dielectrics are used to increase a capacitor's capacitance.

1. Chapter 19
Electric Potential Energy
and Electric Potential

2. AP Learning Objectives
ELECTRICITY AND MAGNETISM
 Electrostatics
• Electric field and electric potential (including point charges)
• Students should understand the concept of electric field,
so they can:
• Define it in terms of the force on a test charge.
• Describe and calculate the electric field of a single
point charge.
• Calculate the magnitude and direction of the electric
field produced by two or more point charges.
• Calculate the magnitude and direction of the force on
a positive or negative charge placed in a specified
field.
• Interpret an electric field diagram.
• Analyze the motion of a particle of specified charge
and mass in a uniform electric field.

3. AP Learning Objectives
• Students should understand the concept of electric potential,
so they can:
• Determine the electric potential in the vicinity of one or
more point charges.
• Calculate the electrical work done on a charge or use
conservation of energy to determine the speed of a charge
that moves through a specified potential difference.
• Determine the direction and approximate magnitude of the
electric field at various positions given a sketch of
equipotentials.
• Calculate the potential difference between two points in a
uniform electric field, and state which point is at the higher
potential.
• Calculate how much work is required to move a test charge
from one location to another in the field of fixed point
charges.
• Calculate the electrostatic potential energy of a system of
two or more point charges, and calculate how much work is
required to establish the charge system.

4. Table of Contents
1. Potential Energy
2. The Electric Potential Difference
3. The Electric Potential Difference Created by Point
Charges
4. Equipotential Surfaces and Their Relation to the electric
Field
5. Capacitors and Dielectrics
6. Biomedical Applications of Electric Potential Differences
(AP?)

5. Chapter 19:
Electric Potential Energy
and Electric Potential
Section 1:
Potential Energy

6.  From Gravity
• Energy based on position
• Change in position
• Change in Energy
• Work
( )2
2
1
vmhmg ∆=∆
Potential Energy
BAAB mghmghW −=

7. Electrical Potential Energy
 Same Effect for Electric Force
 Energy present based on position
• Change in position
• Change in Energy
• Remember, unless
otherwise stated, test
charge is positive
FdUE = 2
21
4
1
r
qq
F
o
E
πε
=
r
r
qq
U
o
E 





= 2
21
4
1
πε 





=
r
qq
U
o
E
21
4
1
πε

8. 19.1.1. Two electrons are separated by a distance R. If the distance between the
charges is increased to 2R, what happens to the total electric potential energy
of the system?
a) The total electric potential energy of the system would increase to four times
its initial value.
b) The total electric potential energy of the system would increase to two times its
initial value.
c) The total electric potential energy of the system would remain the same.
d) The total electric potential energy of the system would decrease to one half its
initial value.
e) The total electric potential energy of the system would decrease to one fourth
its initial value.

9. 19.1.2. The electric potential energy for two positive charges of
magnitude q and separated by a distance r is EPE1. What will the
electric potential energy be if one of the charges is completely
removed and replaced by a negative charge of the same magnitude?
a) U2 = 2 × U1
b) U2 = U1
c) U2 = −U1
d) U2 = −2 × U1
e) There is no way to determine this without knowing the value of q.

10. Chapter 19:
Electric Potential Energy
and Electric Potential
Section 2:
The Electric Potential Difference

11. Electric Potential
 Electric Potential is hard to
understand, but easy to
measure.
 The potential energy per unit
charge
 Related to electric potential
energy and the electric field
 Commonly called “Voltage”
 Measured in volts (1V = 1 J/C)

12. The electric potential at a given point is the electric potential energy
of a small test charge divided by the charge itself:
SI Unit of Electric Potential: joule/coulomb = volt (V)
o
AB
o
A
o
B
AB
q
W
qq
VV
−
=−=−
UU
o
AB
o q
W
q
V
−
=
∆
=∆
U
DEFINITION OF ELECTRIC POTENTIAL
o
E
q
U
V =

13. Example 1 Work, Potential Energy, and
Electric Potential
The work done by the electric force as the
test charge (+2.0x10-6
C) moves from A to
B is +5.0x10-5
J.
Find the difference in EPE between these
points.
Determine the potential difference between
these points.
BAABW UU −=
o
AB
o
A
o
B
q
W
qq
V
−
=−=∆
UU
ABW−=
C102.0
J100.5
6-
5
×
×−
=∆
−
V
J100.5 5−
×−=
(a)
(b)
V25−=

14. Conceptual Example 2 The Accelerations of Positive and Negative Charges
A positive test charge is released from A and accelerates towards B. Upon
reaching B, the test charge continues to accelerate toward C. Assuming that
only motion along the line is possible, what will a negative test charge do when
released from rest at B?
Negative charge will accelerate towards A

15. A positive charge accelerates from a region of higher electric potential
toward a region of lower electric potential.
A negative charge accelerates from a region of lower potential toward
a region of higher potential.
Explanation

16. We now include electric potential energy as part of the total
energy that an object can have:
EUkxmghImvE ++++= 2
2
12
2
12
2
1
ω
One electron volt is the magnitude of the amount by which the potential
energy of an electron changes when the electron moves through a potential
difference of one volt.
V1060.1eV1 19−
×=
Energy Conservation

17. Example 4 The Conservation of Energy
A particle has a mass of 1.8x10-5
kg and a charge of +3.0x10-5
C. It is released
from point A and accelerates horizontally until it reaches point B. The only force
acting on the particle is the electric force, and the electric potential at A is 25V
greater than at B. (a) What is the speed of the particle at point B? (b) If the
same particle had a negative charge and were released from point B, what would
be its speed at A?
AABB UmvUmv +=+ 2
2
12
2
1
BAB UUmv −=2
2
1
( )BAoB VVqmv −=2
2
1
qVU =
( )( ) ( )kg108.1V25C100.32 55 −−
××=Bv
( ) mVVqv BAoB −= 2
sm1.9=Bv
Part b) same speed, opposite direction

18. 19.2.1. Which one of the following statements best explains why it is
possible to define an electrostatic potential in a region of space that
contains an electrostatic field?
a) The work required to bring two charges together is independent of the
path taken.
b) A positive charge will gain kinetic energy as it approaches a negative
charge.
c) Like charges repel one another and unlike charges attract one another.
d) Work must be done to bring two positive charges closer together.
e) A negative charge will gain kinetic energy as it moves away from
another negative charge.

19. 19.2.2. Four point charges are individually brought from infinity and
placed at the corners of a square as shown in the figure. Each
charge has the identical value +Q. The length of the diagonal of the
square is 2a. What is the electric potential at P, the center of the
square?
a)
b)
c) zero volts
d)
e)
a
kQ
4
a
kQ
a
kQ2
a
kQ4

20. Chapter 19:
Electric Potential Energy
and Electric Potential
Section 3:
The Electric Potential Difference
Created by Point Charges

21. Difference in Potential
 What is the potential difference
as a particle moves in an
Electric Field
• due to the electric force as
the point charge moves from
A to B
 Since the force is a function of
distance must use calculus:
dr
r
kqq
W
B
A
r
r
o
∫= 2
∫=
B
A
r
r
o
r
dr
kqqW 2

22. B
o
A
o
r
kqq
r
kqq
−=
o
AB
q
W
V
−
=∆
Total Potential of
All point charges
∑=
i i
i
r
q
kV
Difference in Potential
∫ −=
xx
dx 1
2
∫=
B
A
r
r
o
r
dr
kqqW 2
WU −=∆
oq
U
V
∆
=∆
BA r
kq
r
kq
−=

23. Example 5 The Potential of a Point Charge
Using a zero reference potential at infinity,
determine the amount by which a point charge
of 4.0x10-8
C alters the electric potential at a
spot 1.2m away when the charge is
(a) positive and (b) negative.
r
kq
V =
(a)
(b)
V300−=V
( )( )
m2.1
C100.4CmN1099.8 8229 −
×+⋅×
=V
V300+=V

24. Example 6 The Total Electric Potential
At locations A and B, find the total electric
potential.
( )( ) ( )( )
m60.0
C100.8CmN1099.8
m20.0
C100.8CmN1099.8 82298229 −−
×−⋅×
+
×+⋅×
=AV
( )( ) ( )( )
m40.0
C100.8CmN1099.8
m40.0
C100.8CmN1099.8 82298229 −−
×−⋅×
+
×+⋅×
=BV
∑=
i i
i
r
q
kV
V240+=
V0=

25. Conceptual Example 7 Where is the Potential Zero?
Two point charges are fixed in place. The positive charge is +2q and the
negative charge is –q. On the line that passes through the charges, how
many places are there at which the total potential is zero?

26. 19.3.1. Consider the four arrangements of three point charges. Rank the values of
the total electric potential at point P in each case in descending order (with
the largest first).
a) VA > VD > VC > VB
b) VC > VB > VD > VA
c) VC > VD > VA > VB
d) VB > VC > VB > VA
e) VD > VB > VA > VC

27. 19.3.2. Two point charges lie along the x axis. One charge, located
at the origin, has a magnitude +2q. The other charge of
unknown magnitude and sign is located at x = 5 units. If the
electric potential at x = 4 units is equal to zero volts, what is the
magnitude and sign of the second point charge?
a) −q/2
b) −q/4
c) −2q
d) +q/2
e) +2q

28. Chapter 19:
Electric Potential Energy
and Electric Potential
Section 4:
Equipotential Difference Created by
Point Charges

29. r
kq
V =
Equipotential Surfaces
 An equipotential surface
is a surface on which the
electric potential is the same
everywhere.
 The net electric force does
no work on a charge as it
moves on an equipotential
surface.

30. Electric Field and Equipotential
Surfaces
 The electric field created by
any charge or group of
charges is everywhere
perpendicular to the
associated equipotential
surfaces and points in the
direction of decreasing
potential.

31. Equipotential Surfaces and
Their Relation to the Electric
Field

32. d
V
Eavg −=
In Parallel Plate Capacitors
d

33. Example 9 The Electric Field and Potential
Are Related
The plates of the capacitor are separated by
a distance of 0.032 m, and the potential difference
between them is VB-VA=-64V. Between the
two equipotential surfaces shown in color, there
is a potential difference of -3.0V. Find the spacing
between the two colored surfaces.
ABd
V
E −=
E
V
d −=
m0.032
V64−
= mV100.2 3
×=
mV100.2
V0.3
3
×
−
−= m105.1 3−
×=
dAB

34. 19.4.1. A proton is moved from point B to point A in an electric
field as shown. As a result of its movement, its potential
increases to V. If three protons are moved from point B to A,
how much will the electric potential of the protons increase?
a) V/9
b) V/3
c) V
d) 3V
e) 9V

35. 19.4.2. Which one of the following statements concerning
electrostatic situations is false?
a) No work is required to move a charge along an equipotential
surface.
b) If the electric potential with a region of space is zero volts, the
electric field within that region must also be zero V/m.
c) If a charge is moved along an equipotential surface, there is no
component of the force acting along the charges’ path.
d) The electric field is always perpendicular to equipotential
surfaces.
e) The electric field is zero V/m everywhere inside a conductor.

36. 19.4.3. The drawing shows three point charges of equal magnitude,
but one is positive (shown in blue) and two are negative (shown in
yellow). Some of the equipotential lines surrounding these
charges are shown and five are labeled using letters A, B, C, D,
and E. At which of the labeled points will an electron have the
greatest electric potential energy?
a) A
b) B
c) C
d) D
e) E

37. 19.4.4. The drawing shows three point charges of equal magnitude, but one is positive
(shown in blue) and two are negative (shown in yellow). Some of the equipotential
lines surrounding these charges are shown and five are labeled using letters A, B, C,
D, and E. What is the direction of the electric field at the location of the letter “D?”
a) perpendicular to the equipotential
line marked “D” and directed toward
the negative charge closest to it
b) parallel to the equipotential line
marked “D” and directed toward the
location of the letter “C”
c) perpendicular to the equipotential
line marked “D” and directed toward
the location of the letter “A”
d) toward the negative charge in the lower part of the drawing
e) toward the positive charge

38. Chapter 19:
Electric Potential Energy
and Electric Potential
Section 5:
Capacitors & Dielectrics

39. Capacitors
 A capacitor is a device that can store potential energy
 Usually they are build by placing two conductors near
each other, without touching
 For AP, we will only look at air separating the two plates
• We can make capacitors with other insulators
separating the two conductors.

40. Capacitors and
Dielectrics
 A parallel plate capacitor consists
of two metal plates, one carrying
charge +q and the other carrying
charge –q.
 It is common to fill the region
between the plates with an
electrically insulating substance
called a dielectric.

41.  The magnitude of the charge in each
place of the capacitor is directly
proportional to the magnitude of the
potential difference between the plates.
 The capacitance C is the proportionality
constant.
 SI Unit of Capacitance:
coulomb/volt = farad (F)
VQ ∝
THE RELATION BETWEEN CHARGE AND
POTENTIAL DIFFERENCE FOR A CAPACITOR
V
Q
C =
CVQ =

42. Capacitance
 To determine the capacitance, we
must look at how easily the charge
can flow between the plates
 We will assume that air has the
same permittivity as a vacuum
d
A
C oε
=

43. ENERGY STORAGE IN A CAPACITOR
 The energy stored on a capacitor can be
expressed in terms of the work done by the
battery.
 Voltage represents energy per unit charge,
• so the work to move a charge element dq
from the negative plate to the positive
plate is equal to V dq,
• where V is the voltage on the
capacitor.
 The voltage V is proportional to the amount
of charge which is already on the capacitor.
WdU =
dq
C
q
dU =
VdqdU =

44. ENERGY STORAGE IN A CAPACITOR
 If Q is the amount of charge stored when the whole battery voltage
appears across the capacitor, then the stored energy is obtained
from the integral:
 Since Q=CV, we can rewrite this expression:
∫=
Q
C dq
C
q
U
0 C
Q2
2
1
=
2
2
1
2
1
CVQVUC ==
∫=
Q
dqq
C 0
1

45. 19.5.1. An electrical outlet has two vertical slots and a hole into
which a three prong plug may be inserted. The maximum
potential difference between the two vertical slots is 120 volts.
The hole is connected to earth ground. Estimate the maximum
electric field that exists between the two vertical slots.
a) 240 V/m
b) 4800 V/m
c) 9200 V/m
d) 120 V/m
e) 6300 V/m

46. 19.5.2. The plates of an isolated parallel plate capacitor with a
capacitance C carry a charge Q. What is the capacitance of the
capacitor if the charge is increased to 4Q?
a) C/2
b) C/4
c) 4C
d) 2C
e) C

47. 19.5.3. A parallel plate capacitor with plates of area A and plate
separation d is charged so that the potential difference between
its plates is V. If the capacitor is then isolated and its plate
separation is increased to 2d, what is the potential difference
between the plates?
a) 4V
b) 2V
c) V
d) 0.5V
e) 0.25V

48. 19.5.4. The plates of an isolated parallel plate capacitor with a
capacitance C carry a charge Q. The plate separation is d.
Initially, the space between the plates contains only air. Then,
an isolated metal sheet of thickness 0.5d is inserted between, but
not touching, the plates. How does the potential difference
between the plates change as a result of inserting the metal
sheet?
a) The potential difference will decrease.
b) The potential difference will not be affected.
c) The potential difference will increase.
d) The potential difference will be zero volts.

49. 19.5.5. The plates of an isolated parallel plate capacitor with a
capacitance C carry a charge Q. The plate separation is d. Initially,
the space between the plates contains only air. Then, a Teflon (κ =
2.1) sheet of thickness 0.5d is inserted between, but not touching,
the plates. How does the electric field between the plates change as
a result of inserting the Teflon sheet?
a) The electric field will decrease to approximately one-half its initial
value.
b) The electric field will not be affected.
c) The electric field will increase to approximately twice its initial
value.
d) The electric field will be zero volts per meter.

50. 19.5.6. The plates of an isolated parallel plate capacitor are
separated by a distance d and carry charge of magnitude q. The
distance between the plates is then reduced to d/2. How is the
energy stored in the capacitor affected by this change?
a) The energy increases to twice its initial value.
b) The energy increases to four times its initial value.
c) The energy is not affected by this change.
d) The energy decreases to one fourth of its initial value.
e) The energy decreases to one half of its initial value.

51. 19.5.7. A parallel plate capacitor is connected to a battery that
maintains a constant potential difference across the plates.
Initially, the space between the plates contains only air. Then, a
Teflon (κ = 2.1) sheet is inserted between, but not touching, the
plates. How does the stored energy of the capacitor change as a
result of inserting the Teflon sheet?
a) The energy will decrease.
b) The energy will not be affected.
c) The energy will increase.
d) The energy will be zero joules.