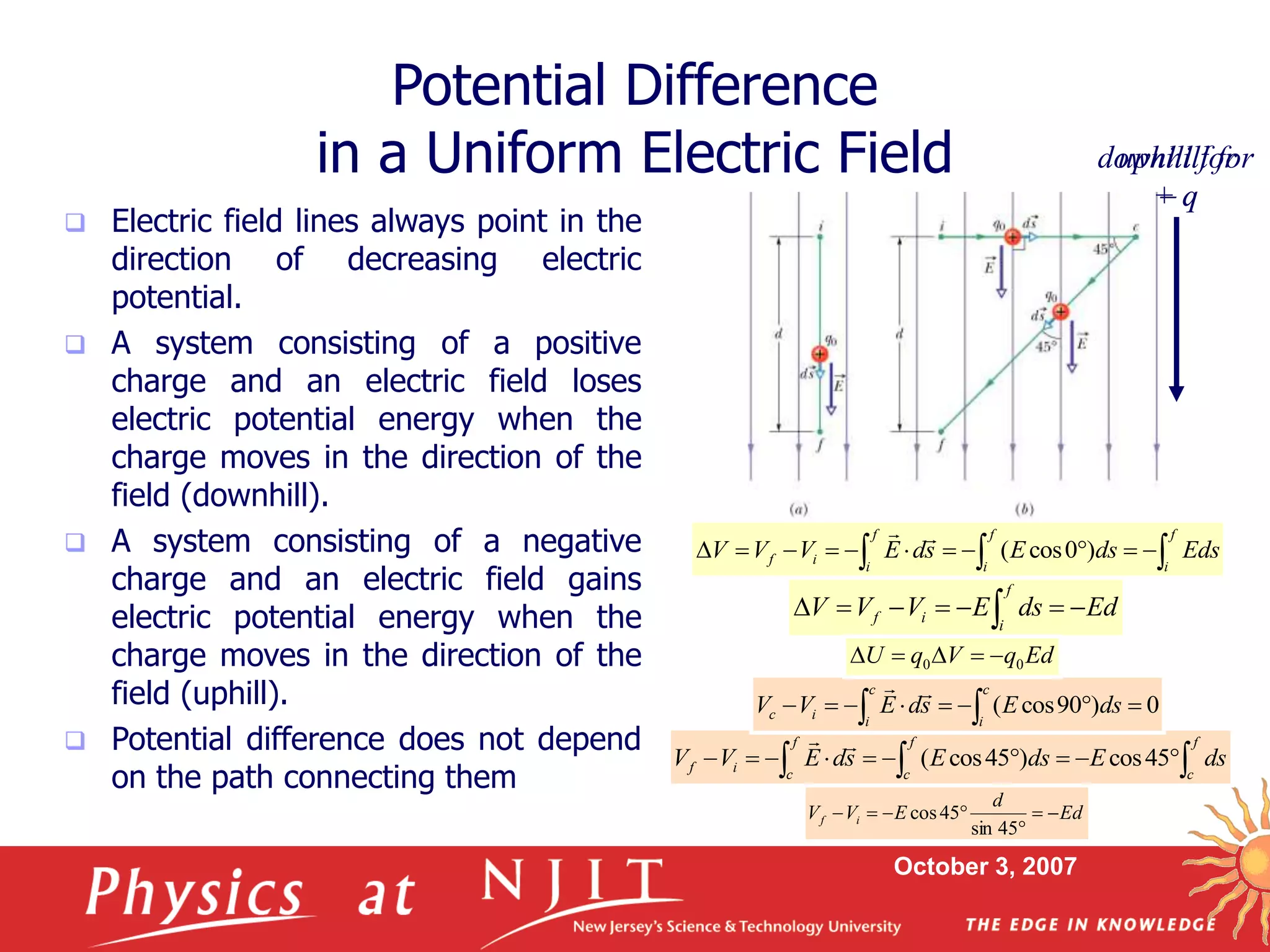
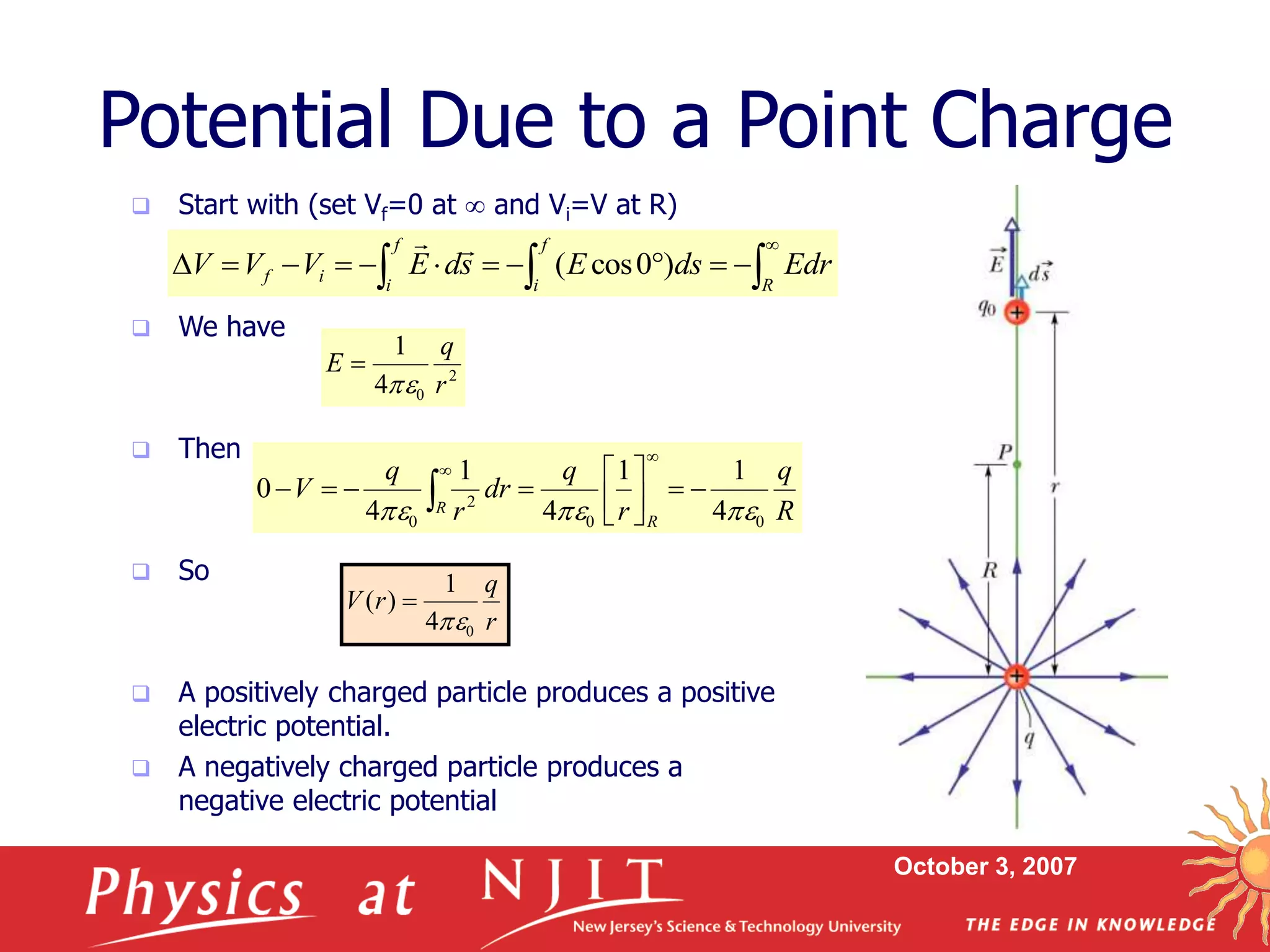
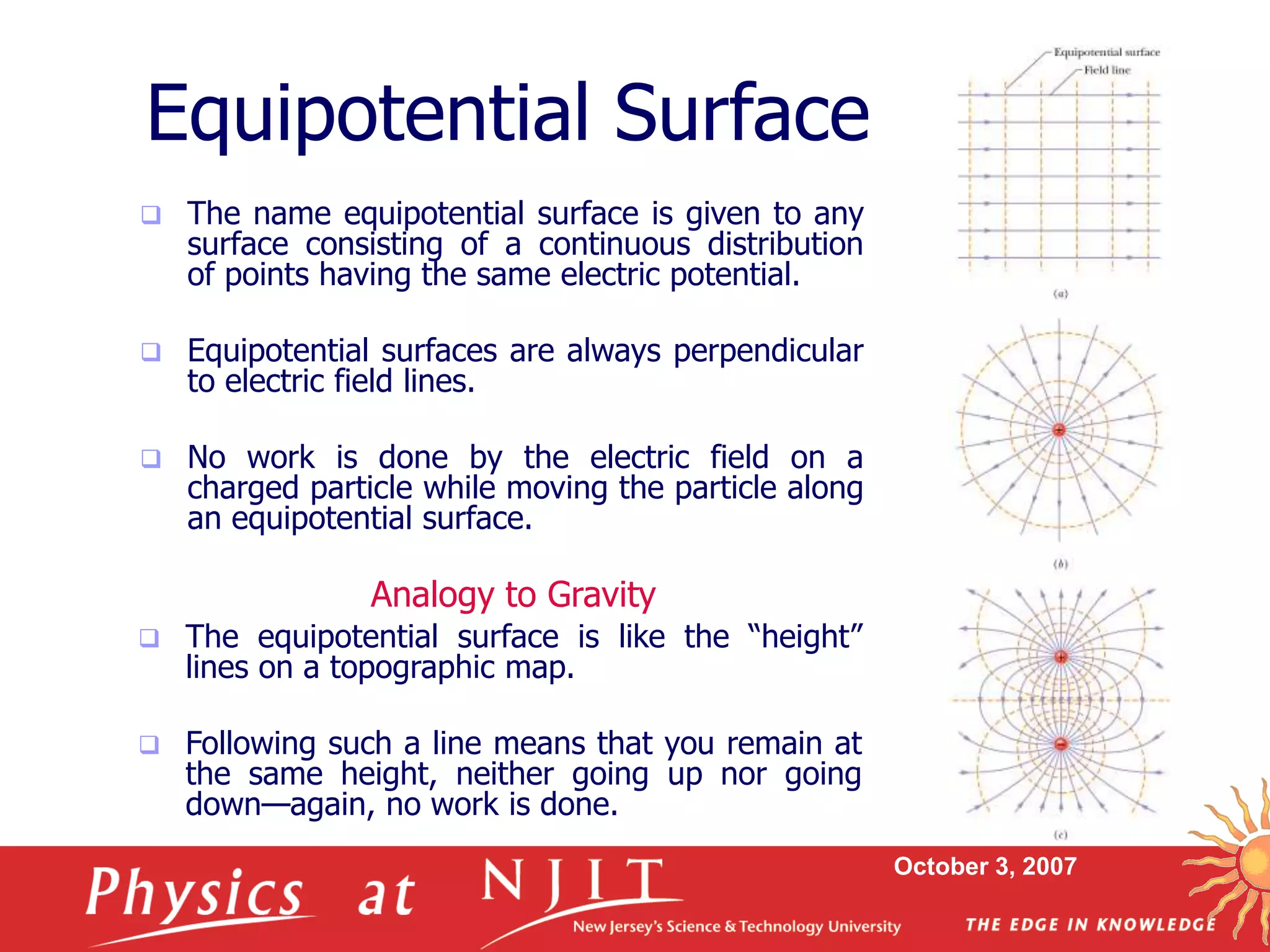
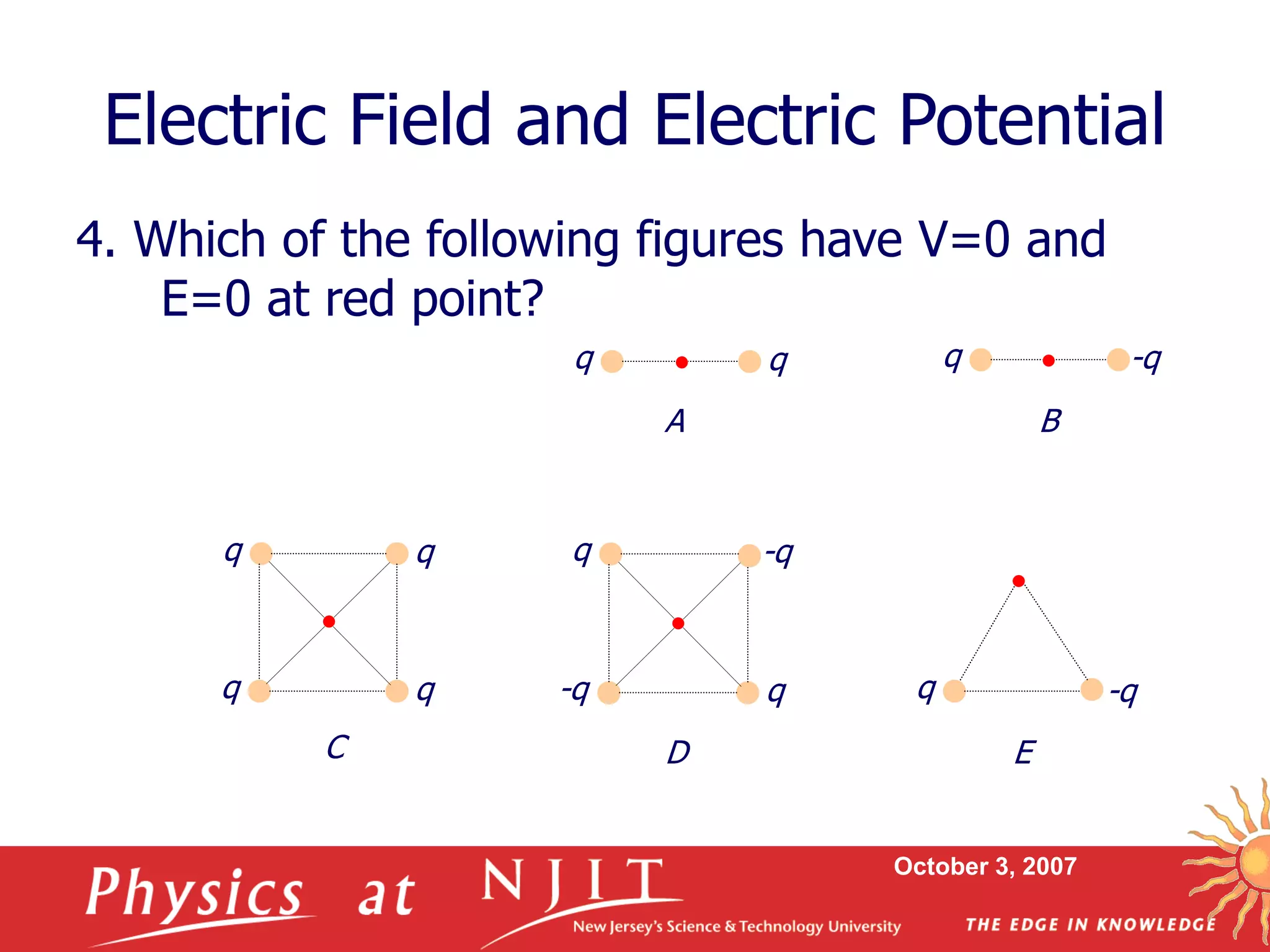
The document summarizes key concepts from a physics lecture on electric potential including: 1. The electric potential (V) at a point is defined as the work (W) done per unit charge to move a test charge from infinity to that point without acceleration. 2. Equipotential surfaces connect all points of equal electric potential. Electric field lines are always perpendicular to equipotential surfaces. 3. Expressions are derived for the electric potential due to point charges, lines of charge, and continuous charge distributions using integration of the electric field.

1. Physics 121: Electricity &
Magnetism – Lecture 5
Electric Potential
Dale E. Gary
Wenda Cao
NJIT Physics Department

2. October 3, 2007
Work Done by a Constant Force
1. The right figure shows four situations in which a force is applied
to an object. In all four cases, the force has the same magnitude,
and the displacement of the object is to the right and of the
same magnitude. Rank the situations in order of the work done
by the force on the object, from most positive to most negative.
A. I, IV, III, II
B. II, I, IV, III
C. III, II, IV, I
D. I, IV, II, III
E. III, IV, I, II
F

I
F

II
F

III
F

IV

3. October 3, 2007
Work Done by a Constant Force
 The work W done a system by
an agent exerting a constant
force on the system is the
product of the magnitude F of
the force, the magnitude Δr of
the displacement of the point
of application of the force, and
cosθ, where θ is the angle
between the force and
displacement vectors:

cos
r
F
r
F
W 






F

II
F

III
r


F

I
r


F

IV
r


r


0

I
W

cos
r
F
WIV 

r
F
WIII 

r
F
WII 



4. October 3, 2007
Potential Energy, Work and
Conservative Force
 Start
 Then
 So
f
i
i
f
g
mgy
mgy
j
y
y
j
mg
r
F
W








 ]
ˆ
)
[(
ˆ


mgy
Ug 
U
U
U
W f
i
g 




g
i
f W
U
U
U 




 The work done by a conservative force
on a particle moving between any two
points is independent of the path
taken by the particle.
 The work done by a conservative force
on a particle moving through any
closed path is zero.
yf
yi
r


g
m


5. October 3, 2007
 The potential energy of the system
 The work done by the electrostatic
force is path independent.
 Work done by a electric force or “field”
 Work done by an Applied force
Electric Potential Energy
Ui
Uf
W
U
U
U i
f 




r
E
q
r
F
W










Ui
Uf
W
W
K
K
K app
i
f 




W
Wapp 
 app
i
f W
U
U
U 




6. October 3, 2007
2. In the right figure, we move the proton from point i to
point f in a uniform electric field directed as shown.
Which statement of the following is true?
A. Electric field does positive work on the proton; And
Electric potential energy of the proton increases.
B. Electric field does negative work on the proton; And
Electric potential energy of the proton decreases.
C. Our force does positive work on the proton; And
Electric potential energy of the proton increases.
D. Electric field does negative work on the proton; And
Electric potential energy of the proton decreases.
E. It changes in a way that cannot be determined.
Work: positive or negative?
E
i
f

7. October 3, 2007
 The electric potential energy
 Start
 Then
 So
 The electric potential
Electric Potential
q
U
V 
q
U
q
U
q
U
V
V
V i
f
i
f







s
d
F
dW




s
d
E
q
dW



 0
s
d
E
q
W
f
i



 
0
 







f
i
i
f s
d
E
q
W
U
U
U


0
 





f
i
s
d
E
q
U
V


0
 Potential difference depends only
on the source charge distribution
(Consider points i and f without
the presence of the test charge;
 The difference in potential energy
exists only if a test charge is
moved between the points.

8. October 3, 2007
 Just as with potential energy, only differences in electric potential are
meaningful.
 Relative reference: choose arbitrary zero reference level for ΔU or ΔV.
 Absolute reference: start with all charge infinitely far away and set Ui = 0,
then we have and at any point in an electric field,
where W is the work done by the electric field on a charged particle as that
particle moves in from infinity to point f.
 SI Unit of electric potential: Volt (V)
1 volt = 1 joule per coulomb
1 J = 1 VC and 1 J = 1 N m
 Electric field: 1 N/C = (1 N/C)(1 VC/J)(1 J/Nm) = 1 V/m
 Electric energy: 1 eV = e(1 V)
= (1.60×10-19 C)(1 J/C) = 1.60×10-19 J
Electric Potential


 W
U q
W
V /




9. October 3, 2007
uphill for
 q
 Electric field lines always point in the
direction of decreasing electric
potential.
 A system consisting of a positive
charge and an electric field loses
electric potential energy when the
charge moves in the direction of the
field (downhill).
 A system consisting of a negative
charge and an electric field gains
electric potential energy when the
charge moves in the direction of the
field (uphill).
 Potential difference does not depend
on the path connecting them
Potential Difference
in a Uniform Electric Field
Ed
ds
E
V
V
V
f
i
i
f 





 
 
 










f
i
f
i
f
i
i
f Eds
ds
E
s
d
E
V
V
V )
0
cos
(


 
 









f
c
f
c
f
c
i
f ds
E
ds
E
s
d
E
V
V 45
cos
)
45
cos
(



 







c
i
c
i
i
c ds
E
s
d
E
V
V 0
)
90
cos
(


Ed
q
V
q
U 0
0 




Ed
d
E
V
V i
f 






45
sin
45
cos
downhill for
+ q

10. October 3, 2007
Equipotential Surface
 The name equipotential surface is given to any
surface consisting of a continuous distribution
of points having the same electric potential.
 Equipotential surfaces are always perpendicular
to electric field lines.
 No work is done by the electric field on a
charged particle while moving the particle along
an equipotential surface.
 The equipotential surface is like the “height”
lines on a topographic map.
 Following such a line means that you remain at
the same height, neither going up nor going
down—again, no work is done.
Analogy to Gravity

11. October 3, 2007
3. The right figure shows a family of equipotential surfaces
associated with the electric field due to some distribution of
charges. V1=100 V, V2=80 V, V3=60 V, V4=40 V. WI, WII, WIII
and WIV are the works done by the electric field on a charged
particle q as the particle moves from one end to the other. Which
statement of the following is not true?
A. WI = WII
B. WIII is not equal to zero
C. WII equals to zero
D. WIII = WIV
E. WIV is positive
Work: positive or negative?

12. October 3, 2007
Potential Due to a Point Charge
 Start with (set Vf=0 at  and Vi=V at R)
 We have
 Then
 So
 A positively charged particle produces a positive
electric potential.
 A negatively charged particle produces a
negative electric potential
2
0
4
1
r
q
E


2
0
4
1
r
q
E


 













f
i R
f
i
i
f Edr
ds
E
s
d
E
V
V
V )
0
cos
(


r
q
r
V
0
4
1
)
(


R
q
r
q
dr
r
q
V
R
R
0
0
2
0 4
1
1
4
1
4
0



















13. October 3, 2007
Potential due to
a group of point charges
 Use superposition
 For point charges
 The sum is an algebraic sum, not a vector sum.
 E may be zero where V does not equal to zero.
 V may be zero where E does not equal to zero.


 










n
i
i
n
i
r
i
r
V
s
d
E
s
d
E
V
1
1





 



n
i i
i
n
i
i
r
q
V
V
1
0
1 4
1

q q
q -q

14. October 3, 2007
4. Which of the following figures have V=0 and
E=0 at red point?
Electric Field and Electric Potential
A
q -q
B
q q
q q
q q
C D
q
E
-q
q -q
-q q

15. October 3, 2007
 Find an expression for dq:
 dq = λdl for a line distribution
 dq = σdA for a surface distribution
 dq = ρdV for a volume distribution
 Represent field contributions at P due to point
charges dq located in the distribution.
 Integrate the contributions over the whole
distribution, varying the displacement as needed,
Potential due to a Continuous
Charge Distribution
r
dq
dV
0
4
1



 

r
dq
dV
V
0
4
1


16. October 3, 2007
 A rod of length L located along the x axis has a uniform linear charge
density λ. Find the electric potential at a point P located on the y axis a
distance d from the origin.
 Start with
 then,
 So
Example: Potential Due to
a Charged Rod
2
/
1
2
2
0
0 )
(
4
1
4
1
d
x
dx
r
dq
dV
dx
dq








 
 
 
 
d
d
L
L
d
x
x
d
x
dx
dV
V
L
L
ln
)
(
ln
4
)
(
ln
4
)
(
4
2
/
1
2
2
0
0
2
/
1
2
2
0
0
2
/
1
2
2
0









 












 


d
d
L
L
V
2
/
1
2
2
0
)
(
ln
4


17. October 3, 2007
 According to Gauss’ law, the charge resides on the
conductor’s outer surface.
 Furthermore, the electric field just outside the
conductor is perpendicular to the surface and field
inside is zero.
 Since
 Every point on the surface of a charged conductor
in equilibrium is at the same electric potential.
 Furthermore, the electric potential is constant
everywhere inside the conductor and equal to its
value to its value at the surface.
Potential Due to
a Charged Isolated Conductor
0




 
B
A
A
B s
d
E
V
V



18. October 3, 2007
s
d
E
q
W



 0
 Suppose that a positive test charge q0 moves through a displacement ds
from on equipotential surface to the adjacent surface.
 The work done by the electric field on the test charge is W = dU = -q0 dV.
 The work done by the electric field may also be written as
 Then, we have
 So, the component of E in any direction is the negative
of the rate at which the electric potential changes with
distance in that direction.
 If we know V(x, y, z),
Calculating the Field from the Potential
z
V
Ez




x
V
Ex




ds
E
q
dV
q )
(cos
0
0 


ds
dV
E 


cos
s
V
Es




y
V
Ey





19. October 3, 2007
Electric Potential Energy
of a System of Point Charges
 Start with (set Ui=0 at  and Uf=U at r)
 We have
 If the system consists of more than two charged
particles, calculate U for each pair of charges and
sum the terms algebraically.
r
q
V 1
0
4
1


r
q
q
V
q
U 2
1
0
2
4
1



)
(
4
1
23
3
2
13
3
1
12
2
1
0
23
13
12
r
q
q
r
q
q
r
q
q
U
U
U
U 






W
Wapp 
 app
i
f W
U
U
U 



W
U
U
U i
f 



 r
E
q
r
F
W










q1
q2

20. October 3, 2007
Summary
 Electric Potential Energy: a point charge moves from i to
f in an electric field, the change in electric potential
energy is
 Electric Potential Difference between two points i and f in
an electric field:
 Equipotential surface: the points on it all have the same
electric potential. No work is done while moving charge
on it. The electric field is always directed perpendicularly
to corresponding equipotential surfaces.
 Finding V from E:
 Potential due to point charges:
 Potential due to a collection of point charges:
 Potential due to a continuous charge distribution:
 Potential of a charged conductor is constant everywhere
inside the conductor and equal to its value to its value at
the surface.
 Calculatiing E from V:
 Electric potential energy of system of point charges:
W
U
U
U i
f 




q
U
q
U
q
U
V
V
V i
f
i
f







r
q
r
V
0
4
1
)
(



 



n
i i
i
n
i
i
r
q
V
V
1
0
1 4
1


 

r
dq
dV
V
0
4
1

s
V
Es




z
V
Ez




x
V
Ex




y
V
Ey




r
q
q
V
q
U 2
1
0
2
4
1



 





f
i
s
d
E
q
U
V


0