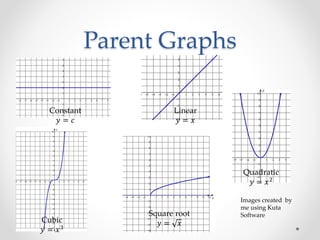
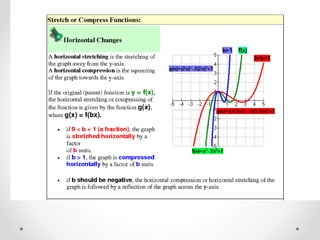
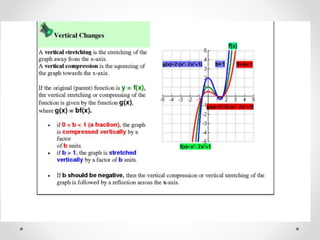
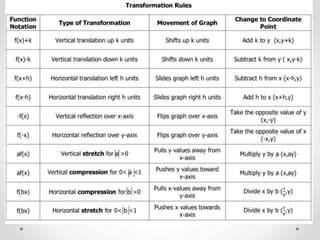
The document discusses transformations and parent graphs. It defines transformations as changes to the position, size, or shape of a figure. Specific transformations covered include translation, reflection, and stretches/compressions. Translation slides points in a direction, reflection flips points across an axis, and stretches/compressions change point distances from an axis. The document also introduces common parent graphs like linear, quadratic, and cubic functions and states the learning targets are applying transformations and identifying parent graphs.

1. Exploring
Transformations
and Parent
Graphs
1-8 and 1-9

2. Learning Targets
• Students will be able to apply and describe
transformations
• Students will be able to identify parent graphs

3. Standards
• Building new functions from existing functions
o identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx),
and f(x + k) for specific values of k (both positive and negative); find the value
of k given the graphs. Experiment with cases and illustrate an explanation of the
effects on the graph using technology. Include recognizing even and odd
functions from their graphs and algebraic expressions for them.
o CCSS.MATH.CONTENT.HSF.BF.B.3

4. Image Notice
• All images used are either made by me or accessed on
google using the labeled for reuse search filter.

5. Parent Graphs
Constant
𝑦 = 𝑐
Linear
𝑦 = 𝑥
Quadratic
𝑦 = 𝑥2
Constant
Cubic
𝑦 = 𝑥3
Square root
𝑦 = 𝑥
Images created by
me using Kuta
Software

6. Transformations:
Translation
• Transformation: Change in the position, size, or shape of
a figure
• Translation: slide each point the same distance in the
same direction.
• Horizontal translations: each point shifts right or left by a
number of units
• Vertical translation: each point shifts up or down by a
number of units
• Note: can have both horizontal and vertical translation—
for example: three units up and two left

7. Transformation:
Reflection
• Reflection across the y-axis
o X coordinate changes, y coordinate stays the same
• Reflection across the x-axis
o Y coordinate changes, x coordinate stays the same

8. Transformation: Stretches
and Compression
• Horizontal stretch: each point is pulled away from the y-
axis
o X coordinate changes
• Horizontal compression: each point is pushed toward the
y-axis
o X coordinate changes
• Vertical stretch: each point is pulled away from the x-axis
o Y coordinate changes
• Vertical compression: each point is pushed toward the x-
axis
o Y coordinate changes