The document discusses Bresenham's line algorithm and how it avoids floating point operations. It explains that the algorithm uses integer arithmetic and a decision parameter to determine the next y-coordinate as it moves across the x-axis in unit intervals. It then describes modifications made to avoid any remaining floating point arithmetic by changing variables and comparisons. The algorithm is faster than other algorithms as it only requires additions and subtractions.

1. How to avoid floating point and multiplication operation in
Bresenham’s algorithm
The idea of Bresenham’s algorithm is to avoid floating point multiplication and
addition to compute mx + c, and then computing round value of (mx + c) in
every step. In Bresenham’s algorithm, we move across the x-axis in unit
intervals.
1. We always increase x by 1, and we choose about next y, whether we
need to go to y+1 or remain on y. In other words, from any position (Xk,
Yk) we need to choose between (Xk + 1, Yk) and (Xk + 1, Yk + 1).
2. We would like to pick the y value (among Yk + 1 and Yk) corresponding to
a point that is closer to the original line.
We need to a decision parameter to decide whether to pick Yk + 1 or Yk as
next point. The idea is to keep track of slope error from previous increment to
y. If the slope error becomes greater than 0.5, we know that the line has
moved upwards one pixel, and that we must increment our y coordinate and
readjust the error to represent the distance from the top of the new pixel –
which is done by subtracting one from error.

2. // Modifying the naive way to use a parameter
// to decide next y.
void withDecisionParameter(x1, x2, y1, y2)
{
m = (y2 - y1)/(x2 - x1)
slope_error = [Some Initial Value]
for (x = x1, y = y1; x = 0.5)
{
y++;
slope_error -= 1.0;
}
}
}
How to avoid floating point arithmetic
The above algorithm still includes floating point arithmetic. To avoid floating
point arithmetic, consider the value below value m.
m = (y2 – y1)/(x2 – x1)
We multiply both sides by (x2 – x1)
We also change slope_error to slope_error * (x2 – x1). To avoid comparison
with 0.5, we further change it to slope_error * (x2 – x1) * 2.
Also, it is generally preferred to compare with 0 than 1.
// Modifying the above algorithm to avoid floating
// point arithmetic and use comparison with 0.
void bresenham(x1, x2, y1, y2)
{
m_new = 2 * (y2 - y1)
slope_error_new = [Some Initial Value]
for (x = x1, y = y1; x = 0)
{
y++;
slope_error_new -= 2 * (x2 - x1);
}
}
}
The initial value of slope_error_new is 2*(y2 – y1) – (x2 – x1). Refer this for
proof of this value

3. Bresenham algorithm is faster than other algorithm :
Bresenham's line drawing algorithm is fast because it reduces determining where
to draw points on a line from the naive y= m*x + b formula to an addition plus a
branch (and the branch can be eliminated through well know branchless integer
techniques). The run-slice version of Brensenham's line drawing algorithm can be
even faster as it determines "runs" of pixels with the same component directly
rather than iterating. Bresenhams algorithm is faster than DDA algorithm in line
drawing because it performs only addition and subtraction in its calculation and
uses only integer arithmetic so it runs significantly faster.
What is shearing in computer graphics
Shearing: A transformation that slants the shape of an object is called
the shear transformation. There are two shear transformations X-Shear and
Y-Shear. One shifts X coordinates values and other shifts Y coordinate
values.

4. Scan Conversion Definition
It is a process of representing graphics objects a collection of pixels. The
graphics objects are continuous. The pixels used are discrete. Each pixel can
have either on or off state.
The circuitry of the video display device of the computer is capable of
converting binary values (0, 1) into a pixel on and pixel off information. 0 is
represented by pixel off. 1 is represented using pixel on. Using this ability
graphics computer represent picture having discrete dots.
Any model of graphics can be reproduced with a dense matrix of dots or
points. Most human beings think graphics objects as points, lines, circles,
ellipses. For generating graphical object, many algorithms have been
developed.
Advantage of developing algorithms for scan
conversion
1. Algorithms can generate graphics objects at a faster rate.
2. Using algorithms memory can be used efficiently.
3. Algorithms can develop a higher level of graphical objects.

5. Examples of objects which can be scan converted
1. Point
2. Line
3. Sector
4. Arc
5. Ellipse
6. Rectangle
7. Polygon
8. Characters
9. Filled Regions
The process of converting is also called as rasterization. The algorithms
implementation varies from one computer system to another computer
system. Some algorithms are implemented using the software. Some are
performed usinghardware or firmware. Some are performed using various
combinations of hardware, firmware, and software.
What is transformation? Type of transformation
What is transformation? In many cases a complex picture can
always be treated as a combination of straight line, circles, ellipse etc.,
and if we are able to generate these basic figures, we can also generate
combinations of them. Once we have drawn these pictures, the need
arises to transform these pictures.
We are not essentially modifying the pictures, but a picture in the center of
the screen needs to be shifted to the top left hand corner, say, or a picture
needs to be increased to twice it's size or a picture is to be turned through
900 . In all these cases, it is possible to view the new picture as really a
new one and use algorithms to draw them, but a better method is, given
their present form, try to get their new counter parts by operating on the
existing data. This concept is called transformation.

6. The three basic transformations are
(i) Translation
(ii) rotation and
(iii) Scaling.
Translation refers to the shifting of a point to some other place, whose
distance with regard to the present point is known. Rotation as the
name suggests is to rotate a point about an axis. The axis can be any of
the coordinates or simply any other specified line also. Scaling is the
concept of increasing (or decreasing) the size of a picture. (in one or in
either directions. When it is done in both directions, the increase or
decrease in both directions need not be same) To change the size of the
picture, we increase or decrease the distance between the end points of the
picture and also change the intermediate points are per requirements.
Translation:
Consider a point P(x1 , y1 ) to be translated to another point Q(x2 , y2 ). If we
know the point value (x2, y2) we can directly shift to Q by displaying the
pixel (x2, y2). On the other hand, suppose we only know that we want to
shift by a distance of Tx along x axis and Ty along Y axis. Then obviously
the coordinates can be derived by x2 =x1 +Tx and Y2 = y1 + Ty .
Suppose we want to shift a triangle with coordinates at A(20,10),
B(30,100) and C(40,70). The shifting to be done by 20 units along x
axis and 10 units along y axis. Then the new triangle will be at A1 (20+20,
10+10) B1 (30+20, 10+10) C1 (40+20, 70+10) In the matrix form [x2 y2 1] =
[x1 y1 1]

7. Rotation
Suppose we want to rotate a point (x1 y1) clockwise through an angle?
about the origin of the coordinate system. Then mathematically we can
show that
x2 = x1cos ? + y1sin? and
y2 = x1sin? - y1cos?
These equations become applicable only if the rotation is about the origin.
In the matrix for [x2 y2 1] = [x1 y1 1]
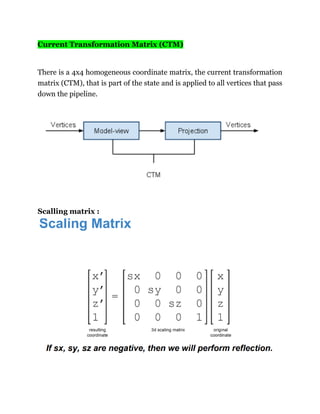
Scaling : Suppose we want the point (x1 y1) to be scaled by a factor sx and
by a factor sy along y direction.
Then the new coordinates become : x2 = x1 * sx and y2 = y1 * sy
(Note that scaling a point physically means shifting a point away. It does
not magnify
the point. But when a picture is scaled, each of the points are scaled
differently and hence the dimensions of the picture changes.)

8. composite transformation in computer graphics
A number of transformations or sequence of transformations can be combined into
single one called as composition. The resulting matrix is called as composite matrix.
The process of combining is called as concatenation.
Suppose we want to perform rotation about an arbitrary point, then we can perform
it by the sequence of three transformations
1. Translation
2. Rotation
3. Reverse Translation
The ordering sequence of these numbers of transformations must not be changed.
If a matrix is represented in column form, then the composite transformation is
performed by multiplying matrix in order from right to left side. The output
obtained from the previous matrix is multiplied with the new coming matrix.

9. Current Transformation Matrix (CTM)
There is a 4x4 homogeneous coordinate matrix, the current transformation
matrix (CTM), that is part of the state and is applied to all vertices that pass
down the pipeline.
Scalling matrix :

10. Matrix notation use in computer graphics
A matrix is an entity composed of components arranged in rows and
columns. Mathematically, a matrix is represented as:
Addition/Subtraction
Matrix addition/subtraction is allowed between matrices that have the same
dimension. To add matrices simply add the corresponding component to each
other.

11. Multiplication
Unlike matrix addition, matrix multiplication does not require matrices to be
of the same dimensions. However, the number of rows in matrix M must be
equal to the number of colums in matrix N. For example:
composite transformation in computer graphics composite transformation incomputer graphics composite transformation in computer graphics