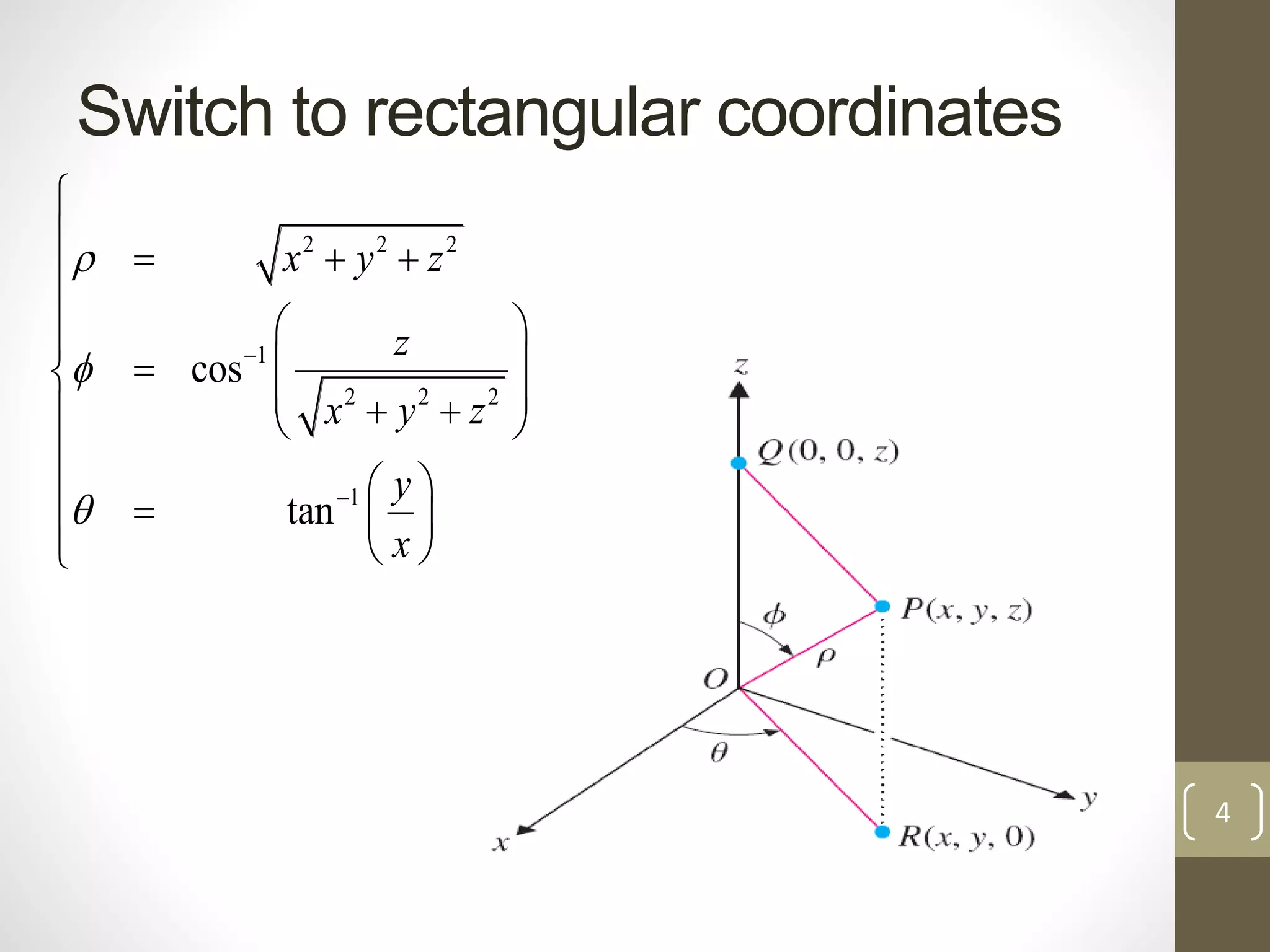
1. The document discusses triple integrals in spherical coordinates. A point in xyz space is characterized by spherical coordinates ρ, θ, and φ which are related to x, y, and z by equations that switch between rectangular and spherical coordinates. 2. A typical triple integral in spherical coordinates has the form of an integral with bounds of ρ from 0 to some value R, θ from 0 to 2π, and φ from 0 to π, integrating a function f(ρ, θ, φ) multiplied by the Jacobian ρ2sin(φ). 3. Switching between rectangular and spherical coordinates involves equations that express x, y, z in terms of ρ, θ, φ or vice versa

1. 1
Name:Viral J. Prajapati
Sem: I
Branch: Electrical
Enrol No:150140109101
Sub: Calculus
Topic:Triple Integrals in Spherical Coordinates

2. Triple Integrals in Spherical
Coordinates
• In spherical cordinates a point in xyz space characterized by
the three coordinates rho, theta, and phi. These are related to
x,y, and z by the equations
• Type equation here.
2
𝝆 ≥ 𝟎 𝟎≤ 𝜽 ≤ 𝟐𝝅 𝟎 ≤ 𝝋 ≤ 𝝅
Recall that

3. Triple Integrals in Spherical Coordinates
•  Switch to spherical coordinates: radius, longitude,
latitude
3
2 2 2 2
sin cos
sin sin
cos
x
y
z
x y z
  
  
 




 
  

4. Switch to rectangular coordinates
4
2 2 2
1
2 2 2
1
cos
tan
x y z
z
x y z
y
x






   

  
      

      

5. 5
 2
sindV d d d    
A typical triple integral in
spherical coordinates has
the form
 
    
 
 
 2 2
1 1
,
2
,
, ,
, , sin
G
h g
h g
f x y z dV
f d d d
   
   
       

  