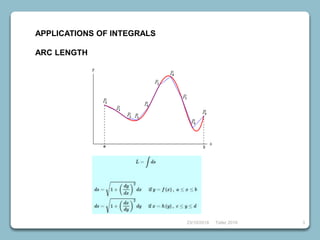
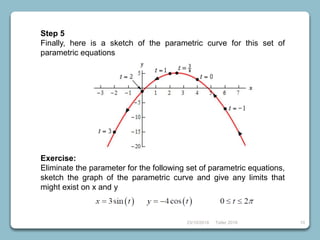
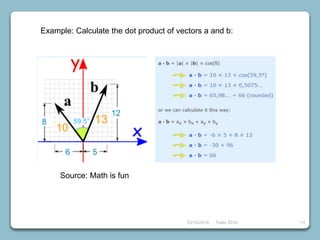
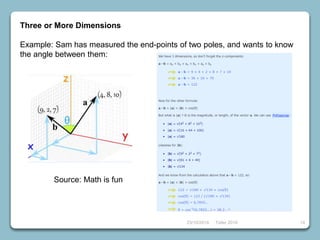
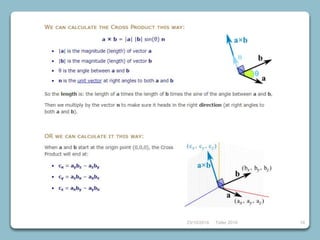
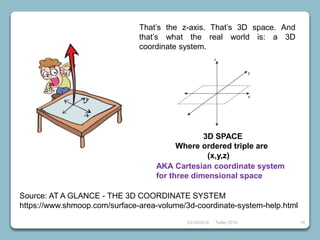
This document contains notes from a calculus workshop covering several topics: 1) Arc length and applications of integrals. 2) Probability density functions and using integrals to find probabilities and means. 3) Parametric equations and eliminating parameters to sketch curves. 4) Vectors, dot products, cross products, and using them to find angles between vectors. 5) Coordinate systems including Cartesian, polar, cylindrical and spherical coordinates. 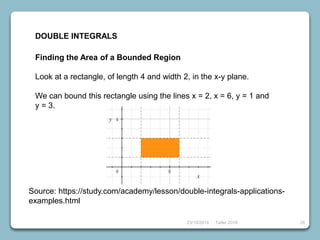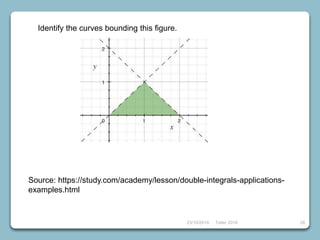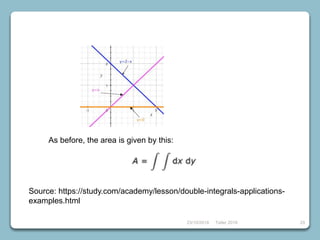6) Double and triple integrals including finding areas, volumes, and changing coordinates.

1. 123/10/2018 Taller 2018

2. 223/10/2018 Taller 2018

3. 23/10/2018 Taller 2018 3
APPLICATIONS OF INTEGRALS
ARC LENGTH

4. 23/10/2018 Taller 2018 4
Determine the length of y = Ln(secx) between 0 ≤ 𝑥 ≤
𝜋
4
Let’s get the derivative out of the way:
𝑑𝑦
𝑑𝑥
=
𝑆𝑒𝑐𝑥. 𝑇𝑎𝑛𝑥
𝑆𝑒𝑐𝑥
= 𝑇𝑎𝑛𝑥
Then
1 + (
𝑑𝑦
𝑑𝑥
)2= 1 + (𝑇𝑎𝑛𝑥)2= (𝑆𝑒𝑐𝑥)2= 𝑆𝑒𝑐𝑥 = 𝑆𝑒𝑐𝑥
We could drop the absolute value bars here since secant is
positive in the range given.
The arc length is then:
𝐿 = 0
𝜋
4 𝑠𝑒𝑐𝑥𝑑𝑥 = 𝐿𝑛 𝑠𝑒𝑐𝑥 + 𝑡𝑎𝑛𝑥 0
𝜋
4
= 𝐿𝑛(1 + 2)
Exercise:
Determine the length of 𝑥 =
2
3
𝑦 − 1
3
2 between 1 ≤ 𝑦 ≤ 4

5. 23/10/2018 Taller 2018 5
APPLICATIONS OF INTEGRALS
PROBABILITY
Every continuous random variable, X, has a probability density
function, f(x). Probability density functions satisfy the following
conditions.
𝟏. 𝒇 𝒙 ≥ 𝟎 for all x.
2. −∞
∞
𝒇 𝒙 𝒅𝒙 = 𝟏

6. 23/10/2018 Taller 2018 6
Let 𝑓 𝑥 =
𝑥3
5000
10 − 𝑥 for 0 ≤ 𝑥 ≤ 10 and for f(x)=0 for all other
values of x. Answer each of the following questions about this function
(a) Show that f(x) is a probability density function
(b) Find 𝑃 1 ≤ 𝑋 ≤ 4
(c) Find 𝑃 𝑥 ≥ 6

7. 23/10/2018 Taller 2018 7
Probability density functions can also be used to determine the
mean of a continuous random variable. The mean is given by
Determine the mean value of X

8. 23/10/2018 Taller 2018 8
PARAMETRIC EQUATIONS AND CURVES
Eliminate the parameter for the following set of parametric
equations, sketch the graph of the parametric curve and give any
limits that might exist on x and y.
𝑥 = 4 − 2𝑡; 𝑦 = 3 + 6𝑡 − 4𝑡2
Step 1
𝑡 =
1
2
4 − 𝑥 → 𝑦 = −𝑥2
+ 5𝑥 − 1
Step 2
we have a parábola that opens downward.
Finally the vertex is
−
𝑏
𝑎
, 𝑓
𝑏
𝑎
= (
5
2
,
21
4
)

9. 23/10/2018 Taller 2018 9
Step 3
One way to get the direction of motion for the curve is to plug in values
of t into the parametric equations to get some points
Step 4
We could sketch the graph at this point, but let’s first get any limits on x
and y that might exist.
Limits on x and y
−∞ < 𝑥 < ∞; 𝑦 ≤
21
4

10. 23/10/2018 Taller 2018 10
Step 5
Finally, here is a sketch of the parametric curve for this set of
parametric equations
Exercise:
Eliminate the parameter for the following set of parametric equations,
sketch the graph of the parametric curve and give any limits that
might exist on x and y

11. 23/10/2018 Taller 2018 11
VECTORS
A vector has magnitude (how long it is) and direction:
Source: Math is fun
DOT PRODUCT
If 𝒂 = 𝒂 𝟏, 𝒂 𝟐, 𝒂 𝟑 𝒂𝒏𝒅 𝒃 = 𝒃 𝟏, 𝒃 𝟐, 𝒃 𝟑
Then the dot product is:
𝒂. 𝒃 = 𝒂 𝟏. 𝒃 𝟏 + 𝒂 𝟐. 𝒃 𝟐 + 𝒂 𝟑. 𝒃 𝟑
We get another number (a scalar) not a new vector

12. 23/10/2018 Taller 2018 12
The Dot Product is written using a central dot:
a · b
This means the Dot Product of a and b
We can calculate the Dot Product of two vectors this way:
a · b = |a| × |b| × cos(θ)
Source: Math is fun
Where:
|a| is the magnitude (length) of vector a
|b| is the magnitude (length) of vector b
θ is the angle between a and b
So we multiply the length of a times the length of b, then multiply by the
cosine of the angle between a and b

13. 23/10/2018 Taller 2018 13
Example: Calculate the dot product of vectors a and b:
Source: Math is fun

14. 23/10/2018 Taller 2018 14
Three or More Dimensions
Example: Sam has measured the end-points of two poles, and wants to know
the angle between them:
Source: Math is fun

15. 23/10/2018 Taller 2018 15
VECTORS
CROSS PRODUCT
Two vectors can be multiplied using the "Cross Product“
The Cross Product axb of two vectors is another vector that is at right
angles to both:

16. 23/10/2018 Taller 2018 16

17. 23/10/2018 Taller 2018 17

18. 23/10/2018 Taller 2018 18
DIMENSIONAL SPACE
3D COORDINATE SYSTEM
How can we envision the 3D coordinate system? Easy. First, we draw
an x-y plane down on a sheet of paper and look down at it.
That’s where all the 2D shapes like triangles and circles and
quadrilaterals live.
2D PLANE
Where the ordered pair/ordered are
(x,y)

19. 23/10/2018 Taller 2018 19
That’s the z-axis. That’s 3D space. And
that’s what the real world is: a 3D
coordinate system.
Source: AT A GLANCE - THE 3D COORDINATE SYSTEM
https://www.shmoop.com/surface-area-volume/3d-coordinate-system-help.html
3D SPACE
Where ordered triple are
(x,y,z)
AKA Cartesian coordinate system
for three dimensional space

20. 23/10/2018 Taller 2018 20
Sample Problem
What's the distance between points T (6, 2, 3) and U (1, 7, -4)?
Where's their midpoint?
Plug 'em. Chug 'em.
Source: AT A GLANCE - THE 3D COORDINATE SYSTEM
https://www.shmoop.com/surface-area-volume/3d-coordinate-system-help.html

21. 23/10/2018 Taller 2018 21
DIMENSIONAL SPACE
POLAR COORDINATES
The Cartesian coordinate of a point are (-8,1). Determine a set of polar
coordinates for the point.
Step 1
We determine r. 𝑟 = 𝑥2 + 𝑦2 = 65
Step2
Let’s get θ 𝜃1 = tan−1 𝑦
𝑥
= −0.1244;𝜃2 = 𝜃1 + 𝜋
( 65,3.0172)
Find the equation of the line y=3x+2 in polar coordinates. We merely
substitute: rsinθ=3rcosθ+2, or r=2sinθ−3cosθ.
Find the equation of the circle (x−1/2)2+y2=1/4 in polar coordinates.

22. 23/10/2018 Taller 2018 22
DIMENSIONAL SPACE
CILINDRICAL COORDINATES
Cylindrical coordinates are a simple extension of the two-dimensional polar
coordinates to three dimensions.
The third cylindrical coordinate is the same as the usual z-coordinate. It is the
signed distance of the point P to the xy-plane (being negative is P is below the
xy-plane). The below figure illustrates the cylindrical coordinates (r,θ,z) of the
point P.
Source: http://tutorial.math.lamar.edu/Classes/CalcIII/CylindricalCoords.aspx

23. 23/10/2018 Taller 2018 23
So, if we have a point in cylindrical coordinates the Cartesian coordinates
can be found by using the following conversions.
If we have a point in Cartesian coordinates the cylindrical coordinates
can be found by using the following conversions
Example 1 Identify the surface for each of the following equations.
a) r = 5
b) r2+z2 = 100
c) z = r
Source:
http://tutorial.math.lamar.edu/Classes/CalcIII/CylindricalCoords.aspx

24. 23/10/2018 Taller 2018 24
DIMENSIONAL SPACE
SPHERICAL COORDINATES
Source: http://tutorial.math.lamar.edu/Classes/CalcIII/SphericalCoords.aspx
Spherical coordinates consist of the following
three quantities:
ρ = This is the distance from the origin to the
point and we will require:ρ≥ 0
Θ = It is the angle between the positive xx-axis
and the line above denoted by r
Φ = This is the angle between the positive zz-axis
and the line from the origin to the point. We will
require 0≤φ≤π

25. 23/10/2018 Taller 2018 25
Example Identify the surface for each of the following equations.
ρ = 5
Φ = π/3
Θ =2π/3
ρsinφ=2
Source: http://tutorial.math.lamar.edu/Classes/CalcIII/SphericalCoords.aspx

26. 23/10/2018 Taller 2018 26
DOUBLE INTEGRALS
Finding the Area of a Bounded Region
Look at a rectangle, of length 4 and width 2, in the x-y plane.
We can bound this rectangle using the lines x = 2, x = 6, y = 1 and
y = 3.
Source: https://study.com/academy/lesson/double-integrals-applications-
examples.html

27. 23/10/2018 Taller 2018 27
Finding this area using a double integral:
The inner integral:
The double integral now becomes this:

28. 23/10/2018 Taller 2018 28
Identify the curves bounding this figure.
Source: https://study.com/academy/lesson/double-integrals-applications-
examples.html

29. 23/10/2018 Taller 2018 29
As before, the area is given by this:
Source: https://study.com/academy/lesson/double-integrals-applications-
examples.html

30. 23/10/2018 Taller 2018 30
The inner integral (which has limits defined by curves which bound the
region) is an integration on x. We fix a y and look at which curves bound
the x values.
For a fixed y, the values of x range from x = y to x = 2 - y. Note that the
formulas for the curves have been rewritten so that x is the subject.
Our inner integral is now:

31. 23/10/2018 Taller 2018 31
Our double integral now becomes:
Note that we can also use double integrals for finding areas of
bounded regions that form more complex shapes, which may not be
as familiar as rectangles or triangles.

32. 23/10/2018 Taller 2018 32
TRIPLE INTEGRALS
It will come as no surprise that we can also do triple integrals—integrals
over a three-dimensional region. The simplest application allows us to
compute volumes in an alternate way.
To approximate a volume in three dimensions, we can divide the three-
dimensional region into small rectangular boxes, each Δx×Δy×Δz with
volume ΔxΔyΔz. Then we add them all up and take the limit, to get an
integral:
If the limits are constant, we are simply computing the volume of a
rectangular box.

33. 23/10/2018 Taller 2018 33
Example: We use an integral to compute the volumen of the box
with opposite corners at (0,0,0) and (1,2,3).
Of course, this is more interesting and useful when the limits are not
constant
Example 2: Find the volumen of the tetrahedron with corners at
(0,0,0), (0,3,0), (2,3,0), and (2,3,5)
Source:
https://www.whitman.edu/mathematics/calculus_online/section15.05.html

34. 23/10/2018 Taller 2018 34
The whole problem comes down to correctly describing the región
by inequalities: 0 ≤ 𝑥 ≤
2,3𝑥
2
≤ 𝑦 ≤ 3,0 ≤ 𝑧 ≤ 5𝑥/2. The lower y limit
comes from the equation of the line y=3x/2 that forms one edge of
the tetrahedron in the x-y plane; the upper z limit comes from the
equation of the plane z=5x/2 that forms the “upper” side of the
tetrahedron. Now the volumen is

35. 23/10/2018 Taller 2018 35
TRIPLE INTEGRAL IN SPHERICAL COORDINATES
Theorem
Remark:
Spherical coordinates are useful when the integration región R is
described in a simple way using spherical coordinates.
Notice the extra factor on the right-hand side.
Source: http://users.math.msu.edu/users/gnagy/teaching/11-
fall/mth234/L29-234-tu.pdf

36. 23/10/2018 Taller 2018 36
TRIPLE INTEGRAL IN SPHERICAL COORDINATES
Source: http://users.math.msu.edu/users/gnagy/teaching/11-
fall/mth234/L29-234-tu.pdf

37. 23/10/2018 Taller 2018 37
Source: http://users.math.msu.edu/users/gnagy/teaching/11-
fall/mth234/L29-234-tu.pdf

38. 3823/10/2018 Taller 2018

39. 39
[1] Calculus II
http://tutorial.math.lamar.edu/Classes/CalcII/Probability.aspx
[2] Triple Integrals
https://www.whitman.edu/mathematics/calculus_online/section15.05.html
[3] Double Integrals: Applications & Examples
https://study.com/academy/lesson/double-integrals-applications-examples.html
[4] Calculus - Integration: Double Integrals (8 of 9) Example 7: Finding the Volume: Paraboloid
https://www.youtube.com/watch?v=lR8xTjZk5bE
[5] At a glance-The 3D Coordinate System
[Online] Available:
https://www.shmoop.com/surface-area-volume/3d-coordinate-system-help.html
[6] Math is fun-Advanced-Dot product
https://www.mathsisfun.com/algebra/vectors-dot-product.html
[7] Integrals in cylindrical, spherical coordinates
[Online] Available:
http://users.math.msu.edu/users/gnagy/teaching/11-fall/mth234/L29-234-tu.pdf
23/10/2018 Taller 2018

40. 4023/10/2018 Taller 2018
THANKS FOR YOUR ATTENTION!
For further information, write us at:
josuedelaguila1@gmail.com