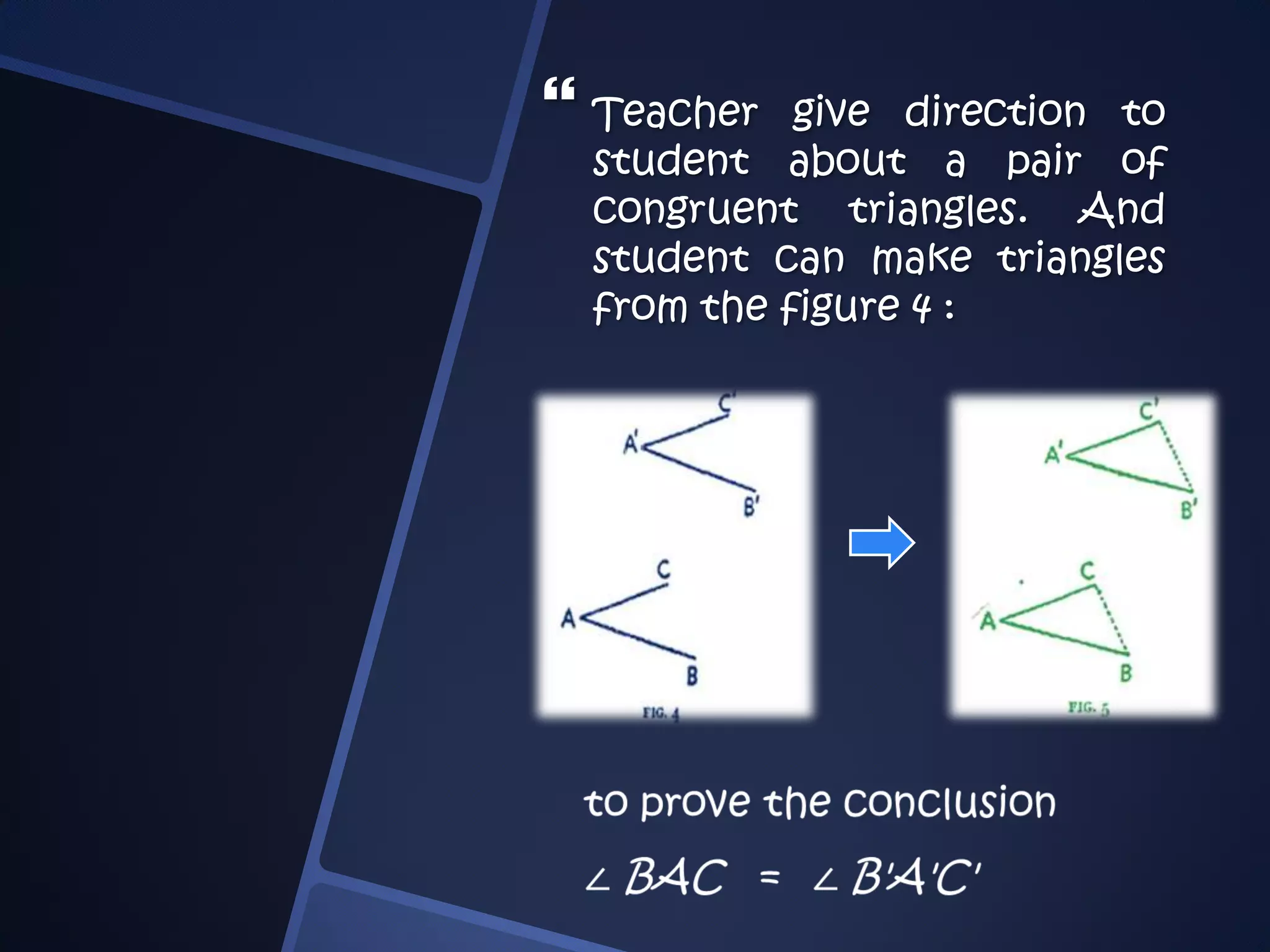
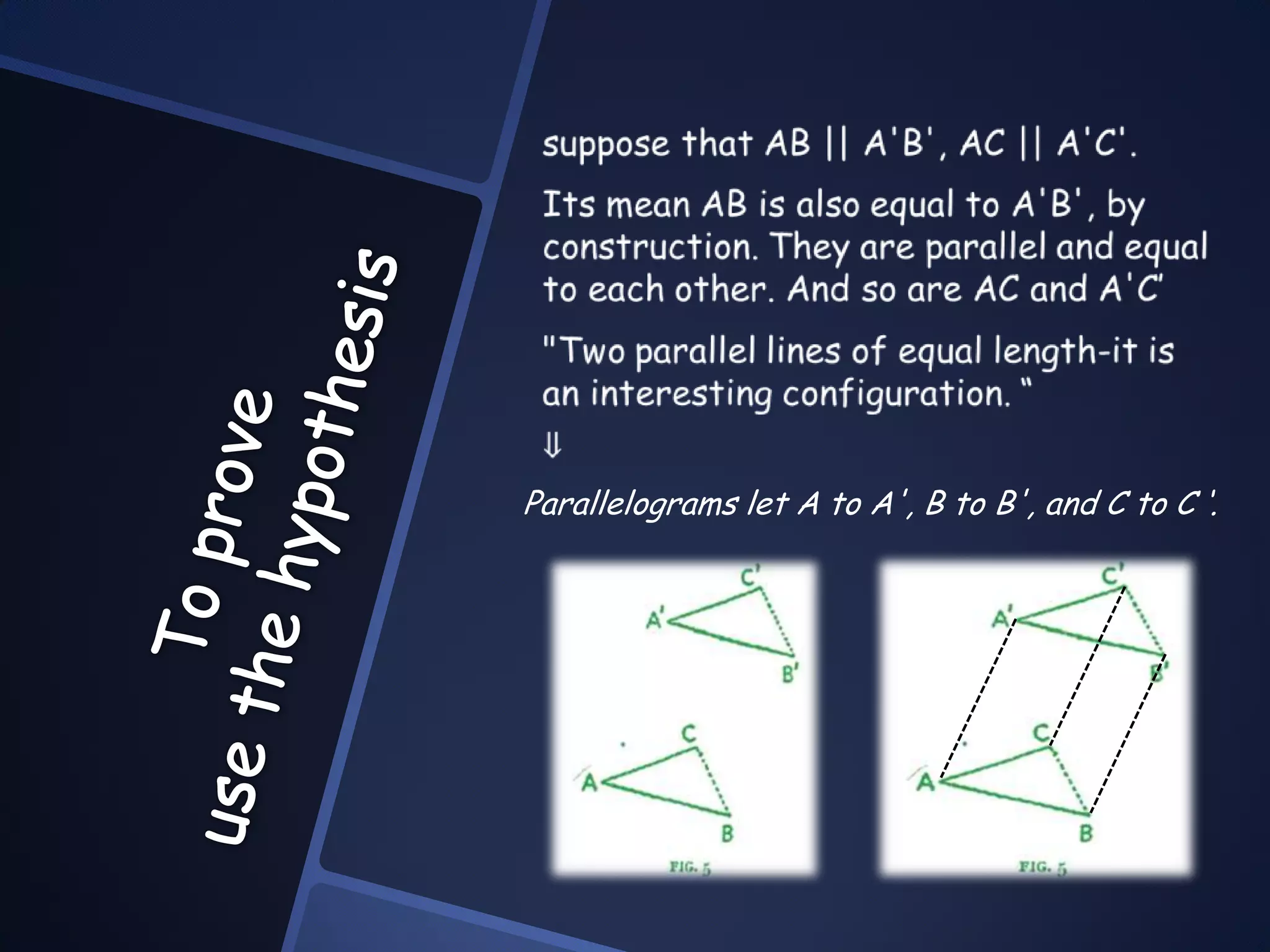
Two angles are in different planes but have corresponding sides that are parallel and have the same direction. This means the angles are equal according to the hypothesis. To prove this, students are instructed to draw the figure and consider forming congruent triangles from the lines, which would mean the corresponding angles are equal based on the triangle congruence theorem stating triangles are congruent if their corresponding sides are equal.

2. Prove that such angles are equal.

3. The Hypothesis :
Two angles are in different
planes but each side of one is
parallel to the corresponding
side of the other, and has also
the same direction
The Conclusion :
The angles are equal

4. The students are asking to
draw the figure consider
hypothesis.
And the figure like below :

5. Consider the figure, the
teacher ask “what is the
hypothesis and conclusion ?”

6. Consider the conclusion,
students are asking to think of
a familiar theorem having the
same or a similar conclusion,
“ If two triangles are congruent,
the corresponding angles are
equal.”

7.  Teacher give direction to
student about a pair of
congruent triangles. And
student can make triangles
from the figure 4 :

8. New aim at a conclusion
“Two triangles are congruent
if only if the three sides of
the one are equal
respectively to the three
sides of the other.”
If we knew that BC = B’C’

10. Parallelograms let A to A', B to B', and C to C ‘.