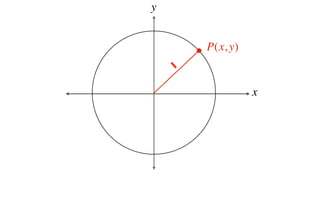
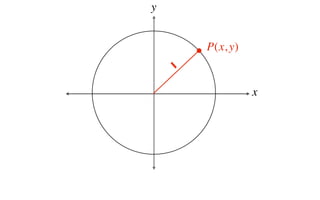
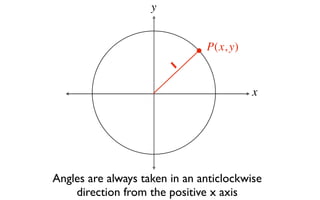
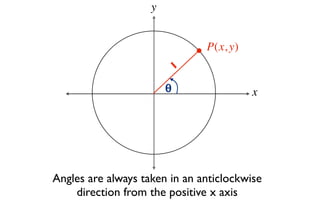
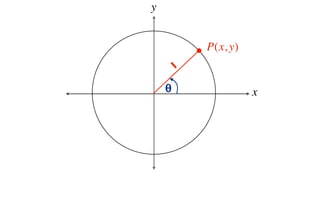
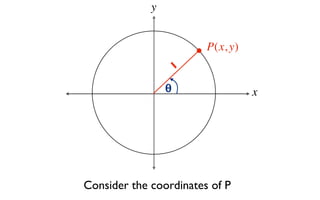
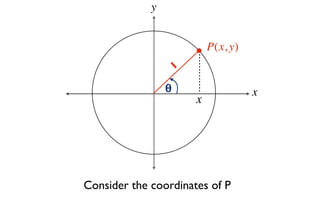
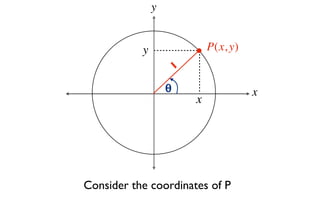
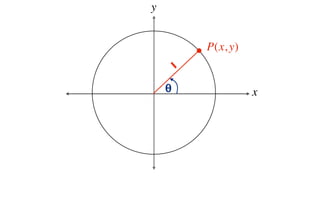
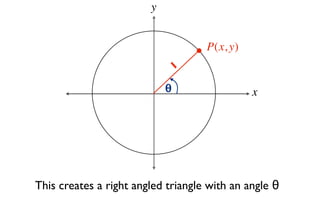
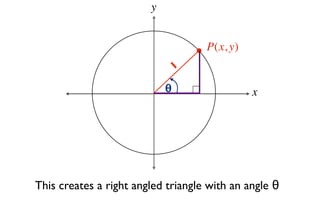
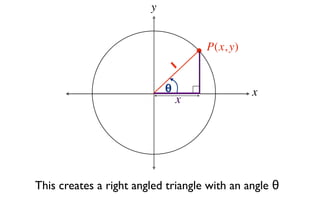
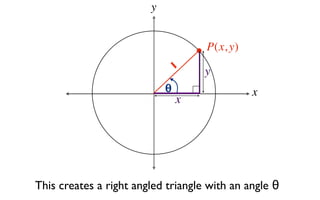
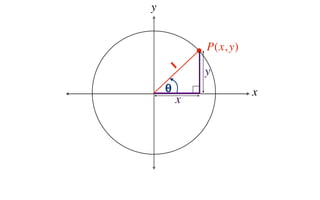
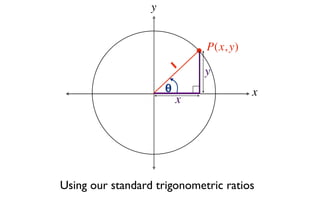
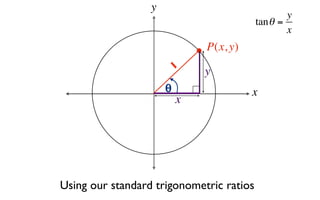
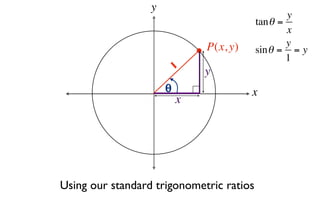
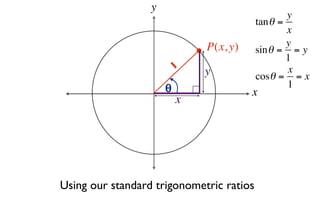
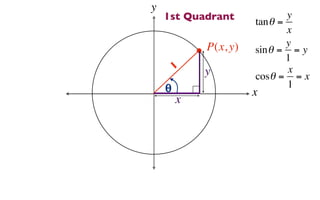
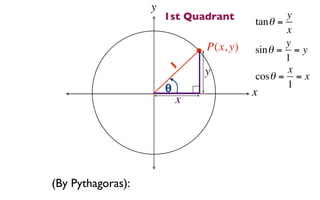
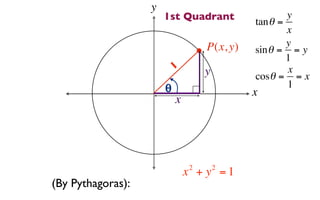
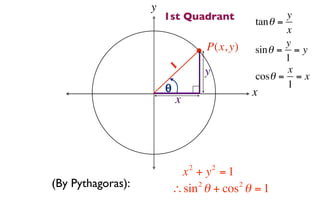
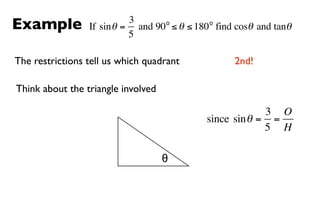
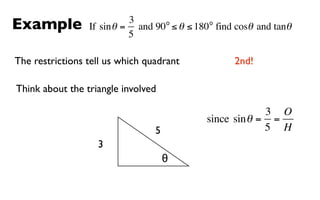
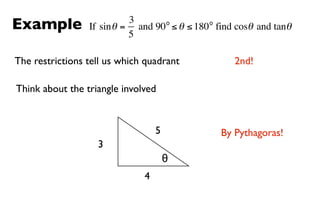
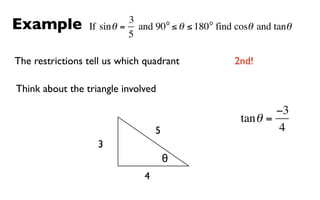
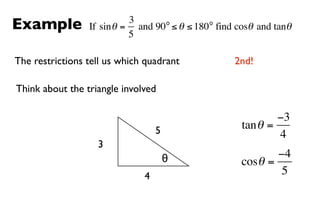
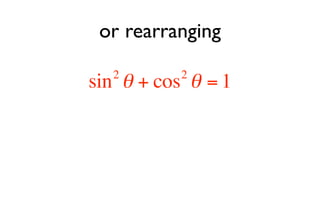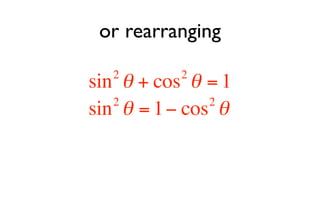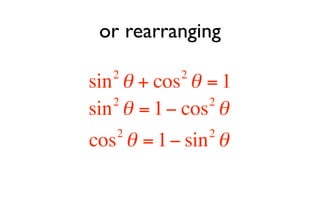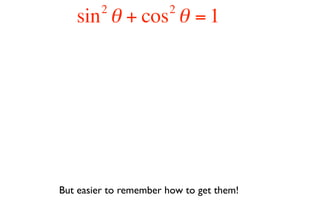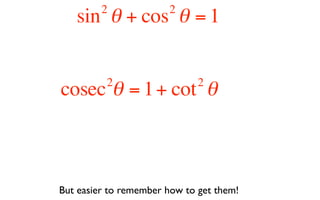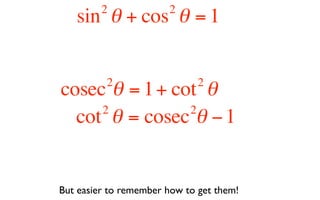This document derives several important trigonometric identities by considering a right triangle with angle θ and using the Pythagorean theorem and definitions of trigonometric functions. It shows that sin2θ + cos2θ = 1, which can be rearranged to obtain other important identities relating sin, cos, tan, sec, and cosec.

1. Trig Identities
Tuesday 14th June 2011

2. y
P(x, y)
1
x

3. y
P(x, y)
1
x

4. y
P(x, y)
1
x
Angles are always taken in an anticlockwise
direction from the positive x axis

5. y
P(x, y)
1
θ x
Angles are always taken in an anticlockwise
direction from the positive x axis

6. y
P(x, y)
1
θ x

7. y
P(x, y)
1
θ x
Consider the coordinates of P

8. y
P(x, y)
1
θ x
x
Consider the coordinates of P

9. y
y P(x, y)
1
θ x
x
Consider the coordinates of P

10. y
P(x, y)
1
θ x

11. y
P(x, y)
1
θ x
This creates a right angled triangle with an angle θ

12. y
P(x, y)
1
θ x
This creates a right angled triangle with an angle θ

13. y
P(x, y)
1
θ x
x
This creates a right angled triangle with an angle θ

14. y
P(x, y)
1 y
θ x
x
This creates a right angled triangle with an angle θ

15. y
P(x, y)
1 y
θ x
x

16. y
P(x, y)
1 y
θ x
x
Using our standard trigonometric ratios

17. y
y
tan θ =
x
P(x, y)
1 y
θ x
x
Using our standard trigonometric ratios

18. y
y
tan θ =
x
P(x, y) y
sin θ = = y
1
1 y
θ x
x
Using our standard trigonometric ratios

19. y
y
tan θ =
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
Using our standard trigonometric ratios

20. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x

21. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
(By Pythagoras):

22. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
2 2
x + y =1
(By Pythagoras):

23. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
2 2
x + y =1
(By Pythagoras): 2 2
∴sin θ + cos θ = 1

24. VERY important Trig Identity

25. VERY important Trig Identity
2 2
sin θ + cos θ = 1

26. or rearranging

27. or rearranging
2 2
sin θ + cos θ = 1

28. or rearranging
2 2
sin θ + cos θ = 1
2 2
sin θ = 1 − cos θ

29. or rearranging
2 2
sin θ + cos θ = 1
2 2
sin θ = 1 − cos θ
2 2
cos θ = 1 − sin θ

30. or dividing both sides

31. or dividing both sides
2 2
sin θ + cos θ = 1

32. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
sin θ sin θ sin θ

33. or dividing both sides

34. or dividing both sides
2 2
sin θ + cos θ = 1

35. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
sin θ sin θ sin θ

36. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
sin θ sin θ sin θ
2 2
∴1 + cot θ = cosec θ

37. or dividing both sides

38. or dividing both sides
2 2
sin θ + cos θ = 1

39. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
sin θ sin θ sin θ

40. or dividing both sides

41. or dividing both sides
2 2
sin θ + cos θ = 1

42. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

43. or dividing both sides

44. or dividing both sides
2 2
sin θ + cos θ = 1

45. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

46. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ

47. or dividing both sides

48. or dividing both sides
2 2
sin θ + cos θ = 1

49. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

50. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ

51. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ
2 2
∴ tan θ = sec θ − 1

52. or dividing both sides

53. or dividing both sides
2 2
sin θ + cos θ = 1

54. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

55. or dividing both sides

56. or dividing both sides
2 2
sin θ + cos θ = 1

57. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

58. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ

59. or dividing both sides

60. or dividing both sides
2 2
sin θ + cos θ = 1

61. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ

62. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ

63. or dividing both sides
2 2
sin θ + cos θ = 1
2 2
sin θ cos θ 1
2
+ 2
= 2
cos θ cos θ cos θ
2 2
∴ tan θ + 1 = sec θ
2 2
∴ tan θ = sec θ − 1

64. But easier to remember how to get them!

65. 2 2
sin θ + cos θ = 1
But easier to remember how to get them!

66. 2 2
sin θ + cos θ = 1
2 2
cosec θ = 1 + cot θ
But easier to remember how to get them!

67. 2 2
sin θ + cos θ = 1
2 2
cosec θ = 1 + cot θ
2 2
cot θ = cosec θ − 1
But easier to remember how to get them!

68. 2 2
sin θ + cos θ = 1
2 2
cosec θ = 1 + cot θ
2 2
cot θ = cosec θ − 1
2 2
sec θ = tan θ + 1
But easier to remember how to get them!

69. 2 2
sin θ + cos θ = 1
2 2
cosec θ = 1 + cot θ
2 2
cot θ = cosec θ − 1
2 2
sec θ = tan θ + 1
2 2
∴ tan θ = sec θ − 1
But easier to remember how to get them!

70. 2 2
sin θ + cos θ = 1
2 2
sin θ = 1 − cos θ
2 2
cosec θ = 1 + cot θ
2 2
cot θ = cosec θ − 1
2 2
sec θ = tan θ + 1
2 2
∴ tan θ = sec θ − 1
But easier to remember how to get them!

71. 2 2
sin θ + cos θ = 1
2 2
sin θ = 1 − cos θ
2 2
cos θ = 1 − sin θ
2 2
cosec θ = 1 + cot θ
2 2
cot θ = cosec θ − 1
2 2
sec θ = tan θ + 1
2 2
∴ tan θ = sec θ − 1
But easier to remember how to get them!

72. Example
Prove
2
1 − sin θ 2
2 2
= cos θ
sin θ + cos θ

73. Example
Prove
2
1 − sin θ 2
2 2
= cos θ
sin θ + cos θ
Only work on one side at a time!

74. Example
Prove
2
1 − sin θ 2
2 2
= cos θ
sin θ + cos θ
2
1 − sin θ
LHS = 2 2
sin θ + cos θ

75. Example
Prove
2
1 − sin θ 2
2 2
= cos θ
sin θ + cos θ
2
1 − sin θ
LHS = 2 2
sin θ + cos θ
2
cos θ
=
1

76. Example
Prove
2
1 − sin θ 2
2 2
= cos θ
sin θ + cos θ
2
1 − sin θ
LHS = 2 2
sin θ + cos θ
2
cos θ
=
1
2
= cos θ

77. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ

78. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ

79. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ
(cosθ )cosθ sin θ (1 − sin θ ) Common
= −
(1 − sin θ )cosθ cosθ (1 − sin θ ) Denominator

80. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ
(cosθ )cosθ sin θ (1 − sin θ )
= −
(1 − sin θ )cosθ cosθ (1 − sin θ )
2 2
cos θ − sin θ + sin θ
=
(1 − sin θ )cosθ

81. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ
(cosθ )cosθ sin θ (1 − sin θ )
= −
(1 − sin θ )cosθ cosθ (1 − sin θ )
2 2
cos θ − sin θ + sin θ
=
(1 − sin θ )cosθ
1 − sin θ
=
(1 − sin θ )cosθ

82. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ
(cosθ )cosθ sin θ (1 − sin θ )
= −
(1 − sin θ )cosθ cosθ (1 − sin θ )
2 2
cos θ − sin θ + sin θ
=
(1 − sin θ )cosθ
1 − sin θ 1
= =
(1 − sin θ )cosθ cosθ

83. Example
cosθ
Prove − tan θ = sec θ
1 − sin θ
cosθ sin θ
LHS = −
1 − sin θ cosθ
(cosθ )cosθ sin θ (1 − sin θ ) Common
= −
(1 − sin θ )cosθ cosθ (1 − sin θ ) Denominator
2 2
cos θ − sin θ + sin θ
=
(1 − sin θ )cosθ
1 − sin θ 1
= = = sec θ
(1 − sin θ )cosθ cosθ

84. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5

85. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant

86. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!

87. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!
Think about the triangle involved
3 O
since sin θ = =
5 H
θ

88. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!
Think about the triangle involved
3 O
since sin θ = =
5 5 H
3
θ

89. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!
Think about the triangle involved
5 By Pythagoras!
3
θ
4

90. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!
Think about the triangle involved
−3
tan θ =
5 4
3
θ
4

91. Example 3 o o
If sin θ = and 90 ≤ θ ≤ 180 find cosθ and tanθ
5
The restrictions tell us which quadrant 2nd!
Think about the triangle involved
−3
5 tan θ =
4
3
θ −4
cosθ =
4 5

92. Now do Ex 8.13