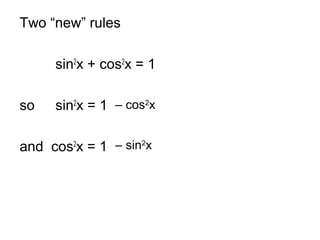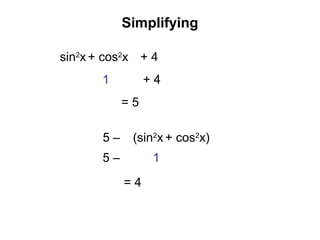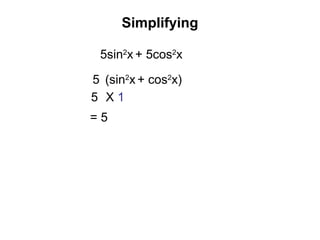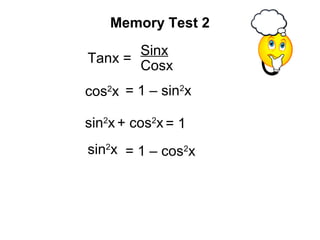Embed presentation
Downloaded 12 times




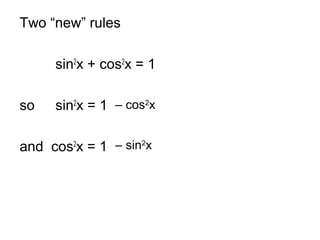


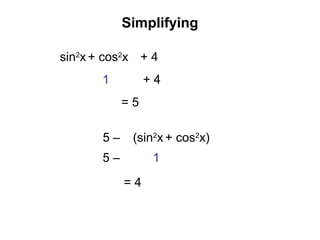
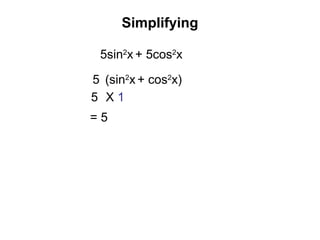





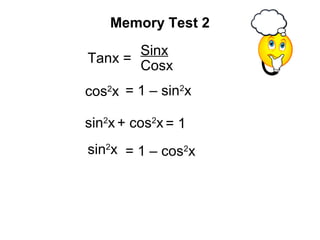

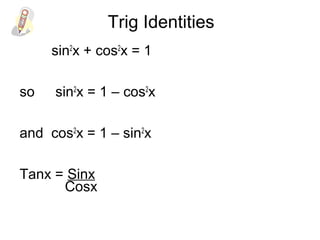

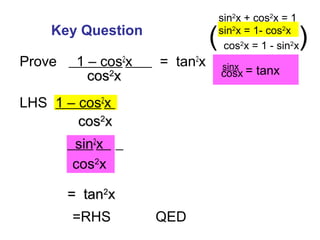
- The document discusses trigonometric identities involving sinx, cosx, and tanx. It introduces the identities sin^2x + cos^2x = 1 and tanx = sinx/cosx. - Examples are provided of using identities to simplify trigonometric expressions. Techniques for proving identities are also demonstrated.