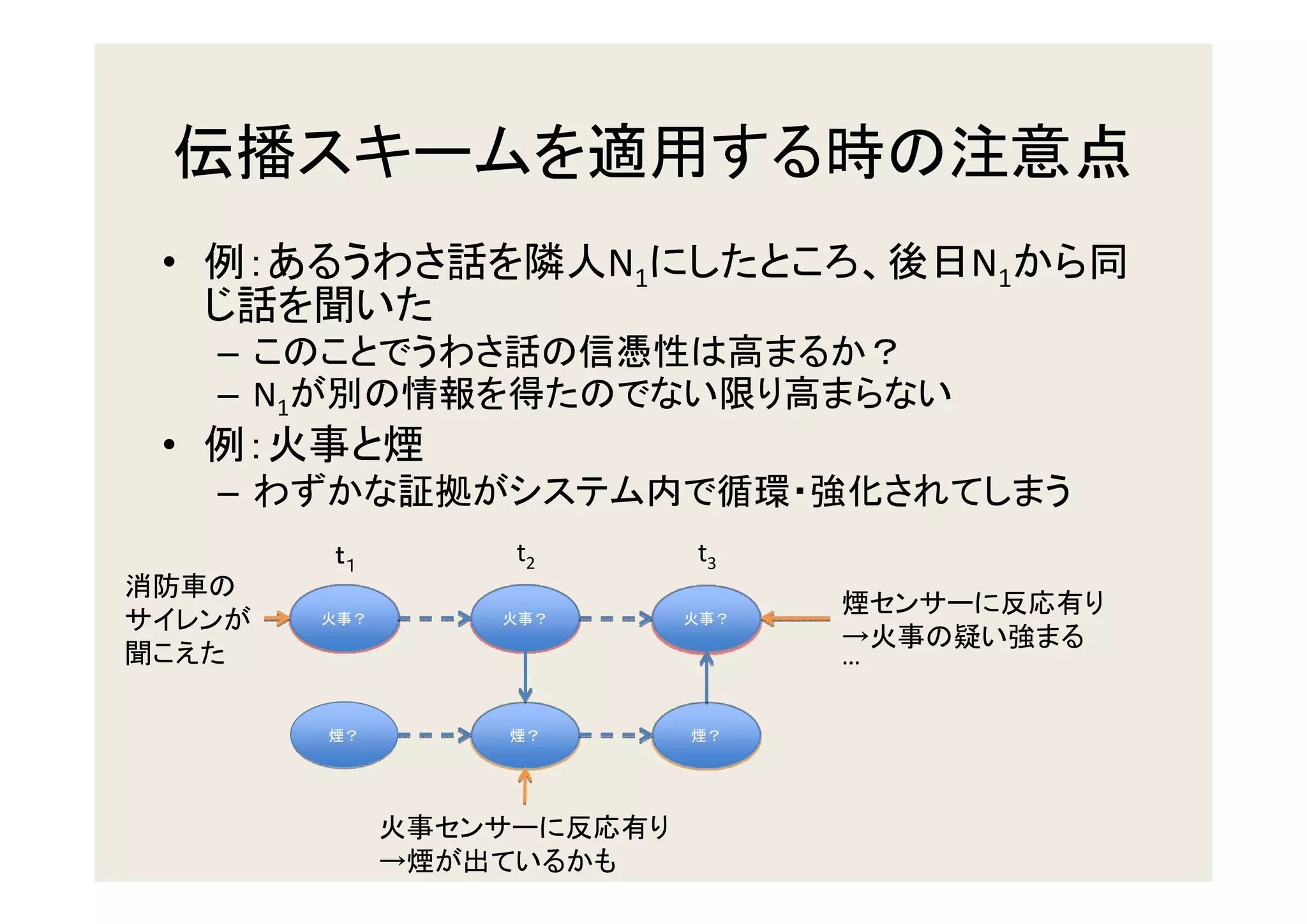
The document discusses probabilistic reasoning in intelligent systems using Bayesian networks. It covers the following topics: 1. Updating beliefs in a network by propagating probabilities between connected nodes using conditional probability tables. 2. Computing the posterior probability at a node given evidence elsewhere in the network by multiplying the prior at the node by the likelihood of the evidence. 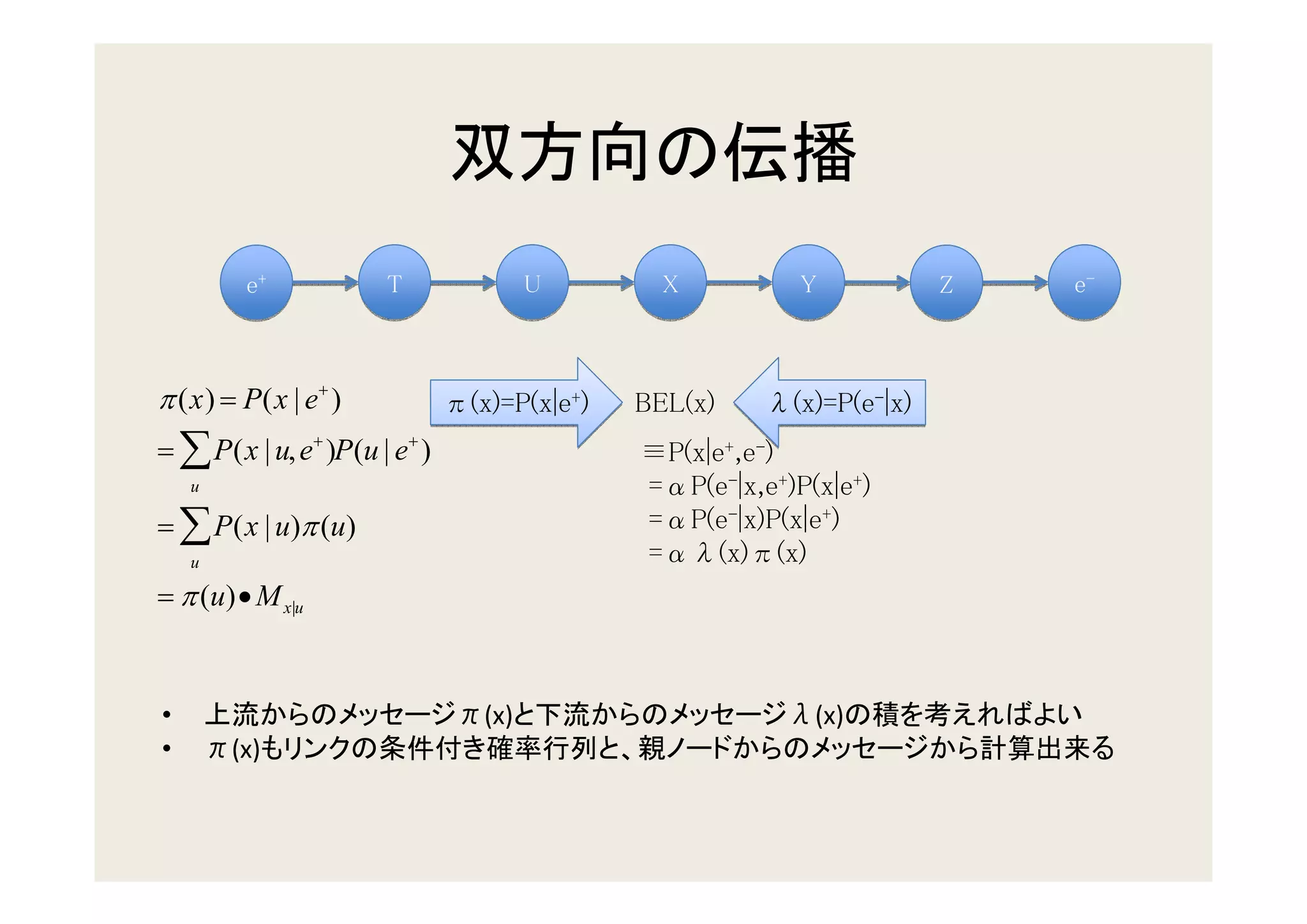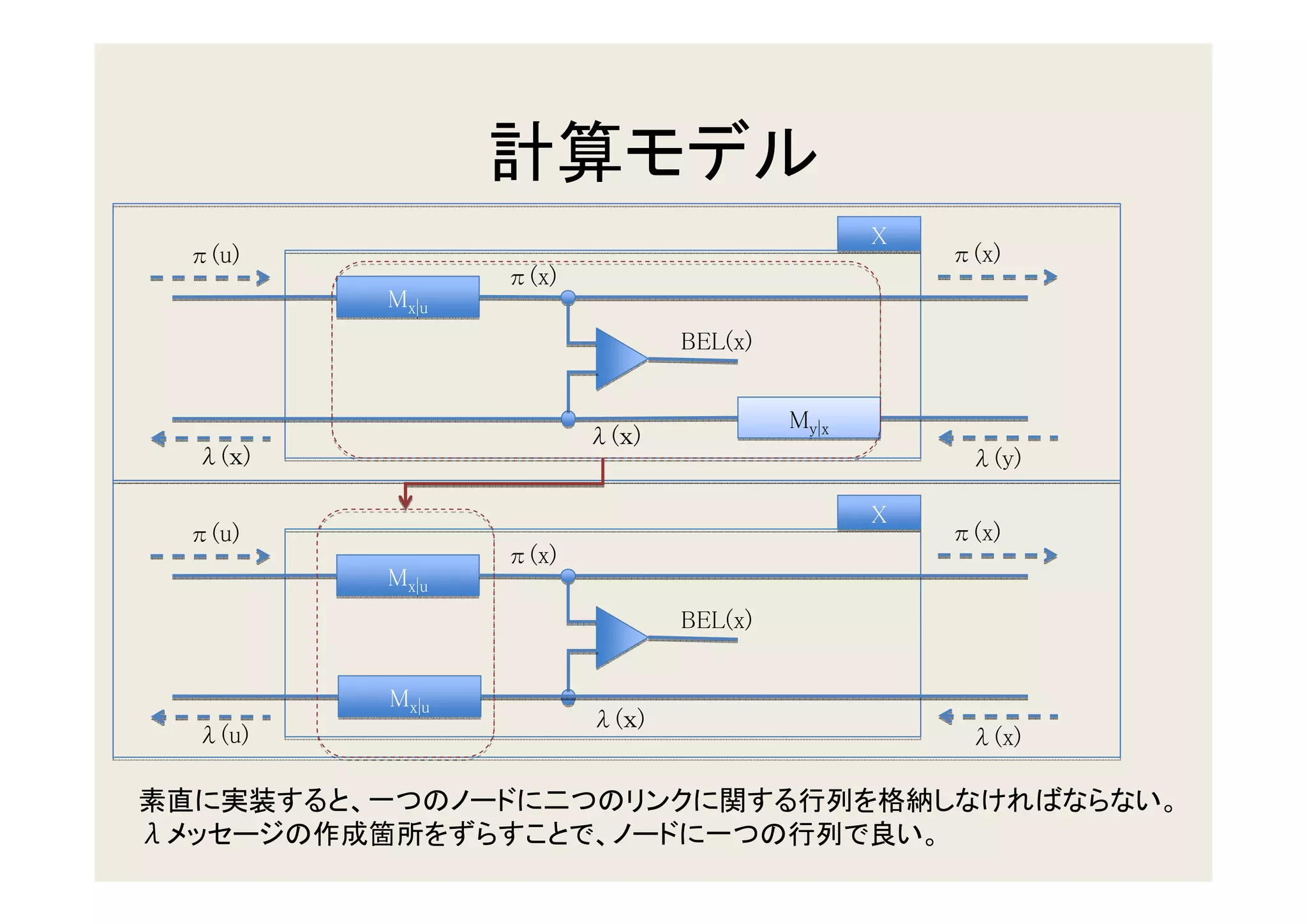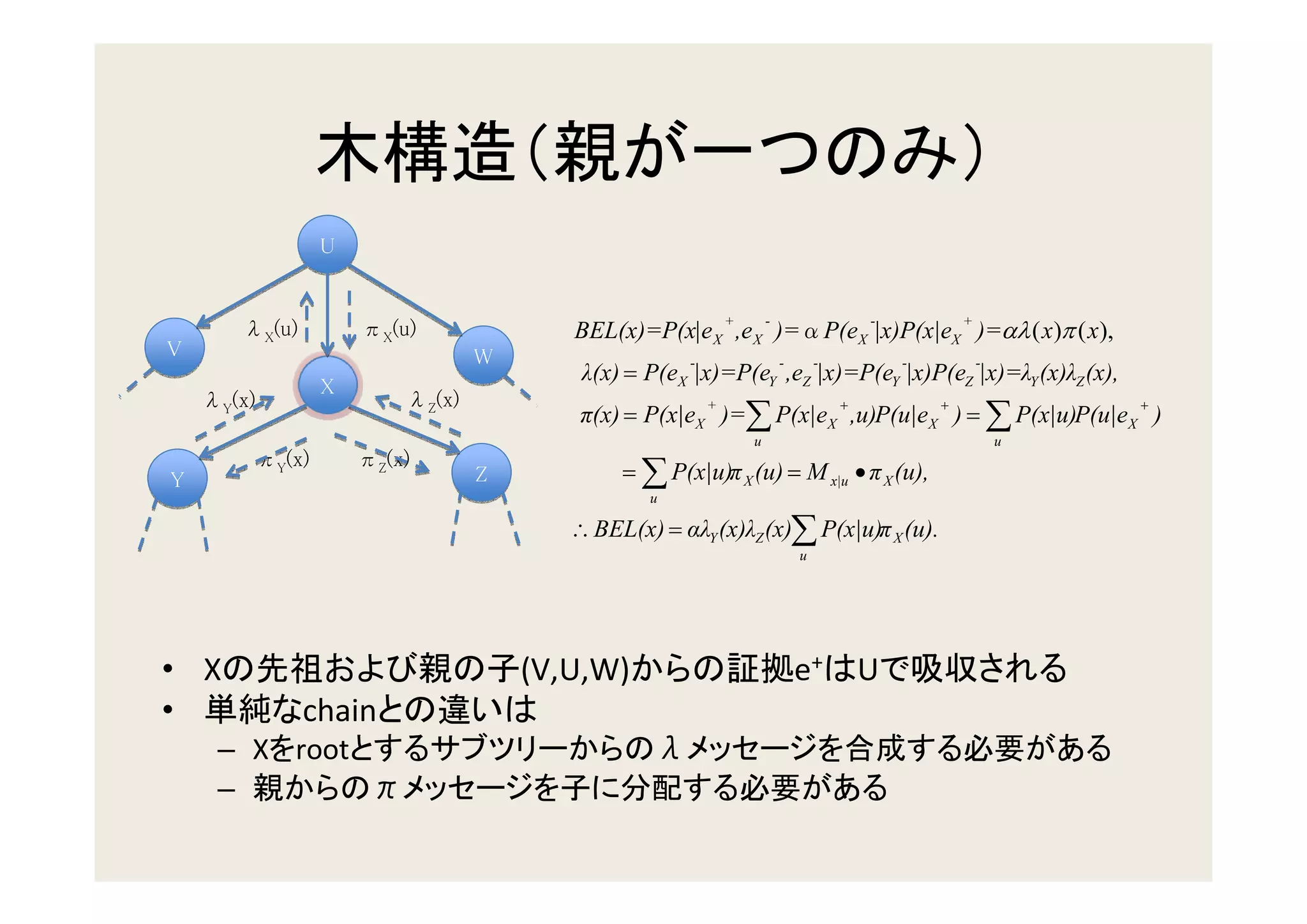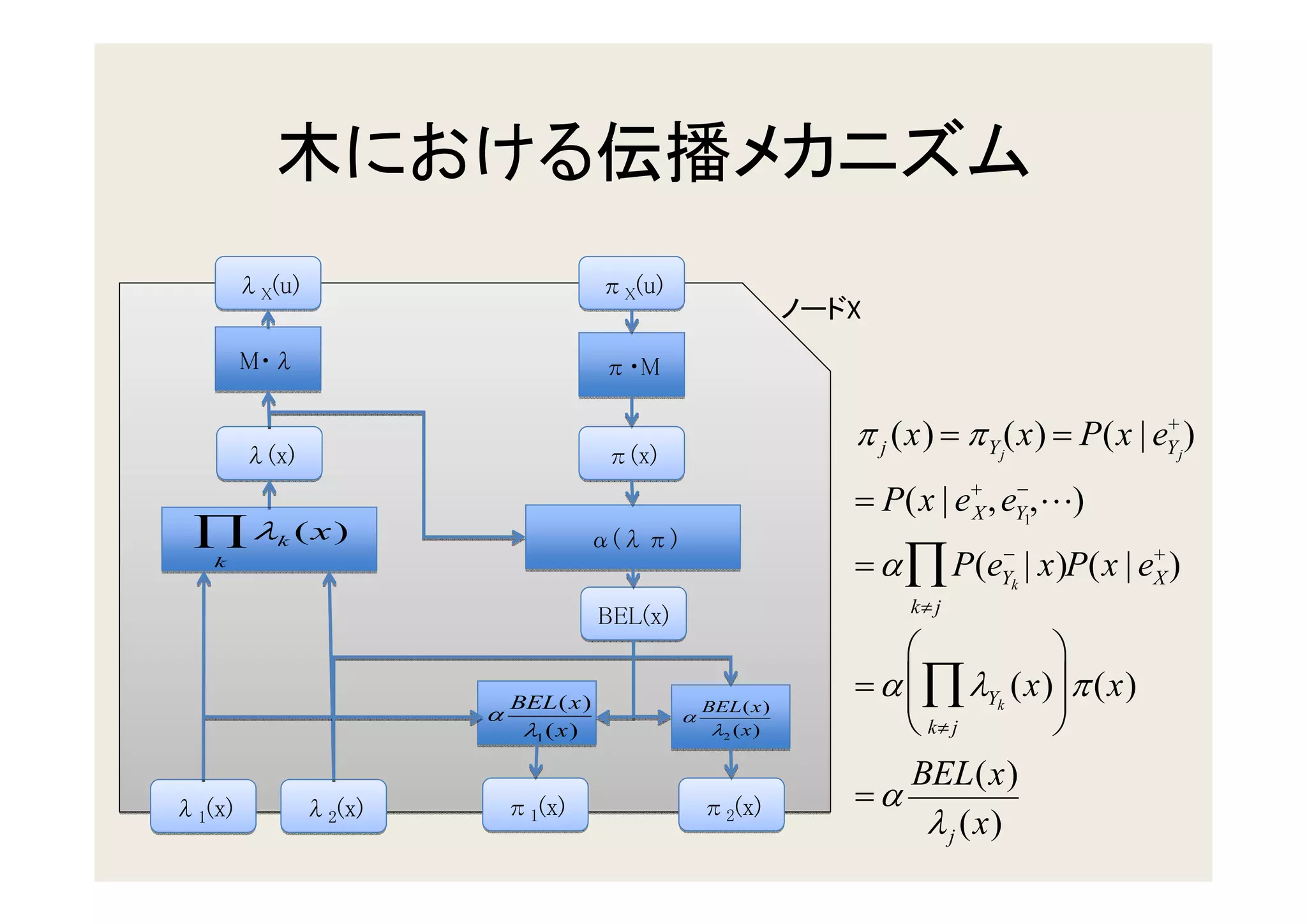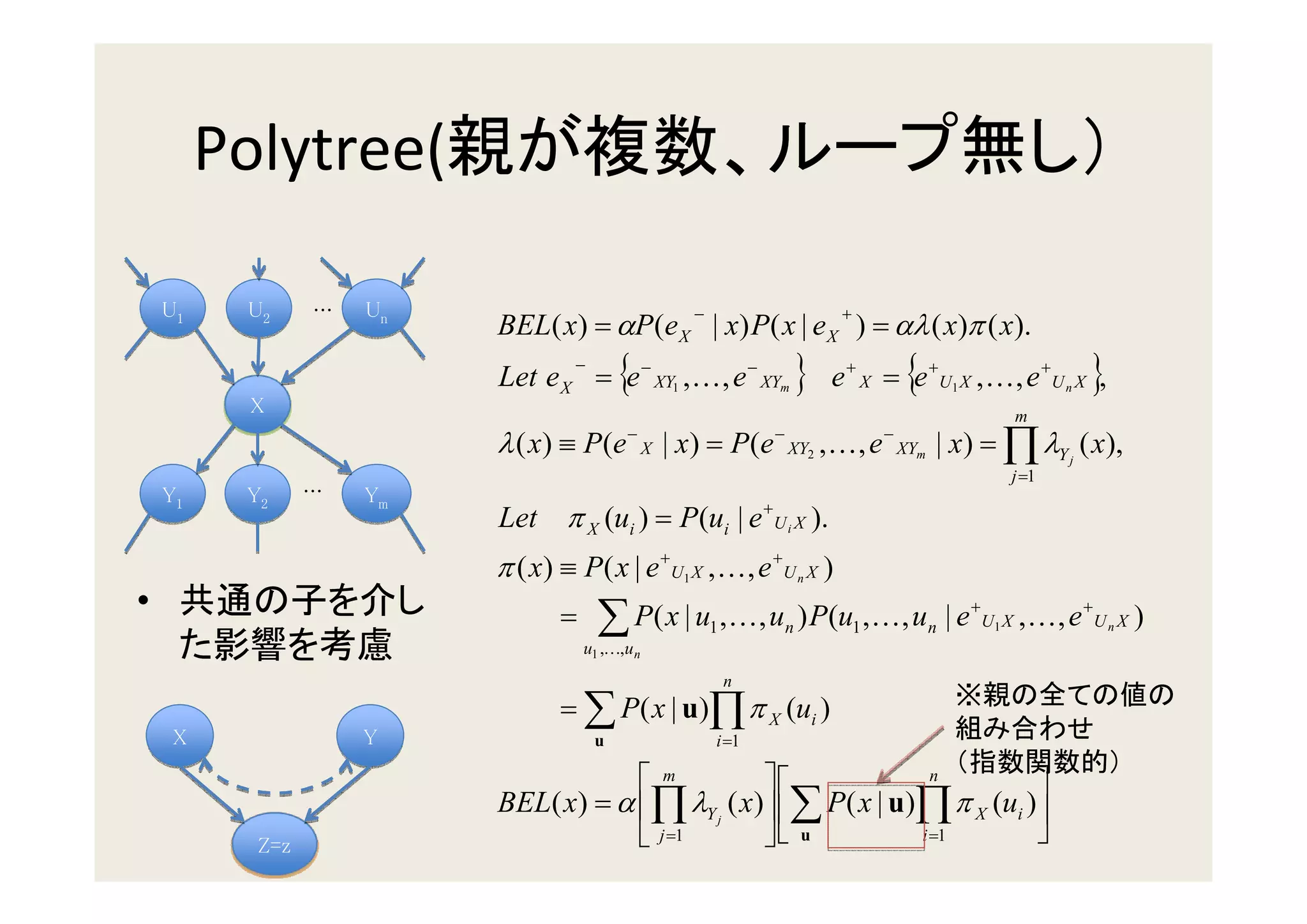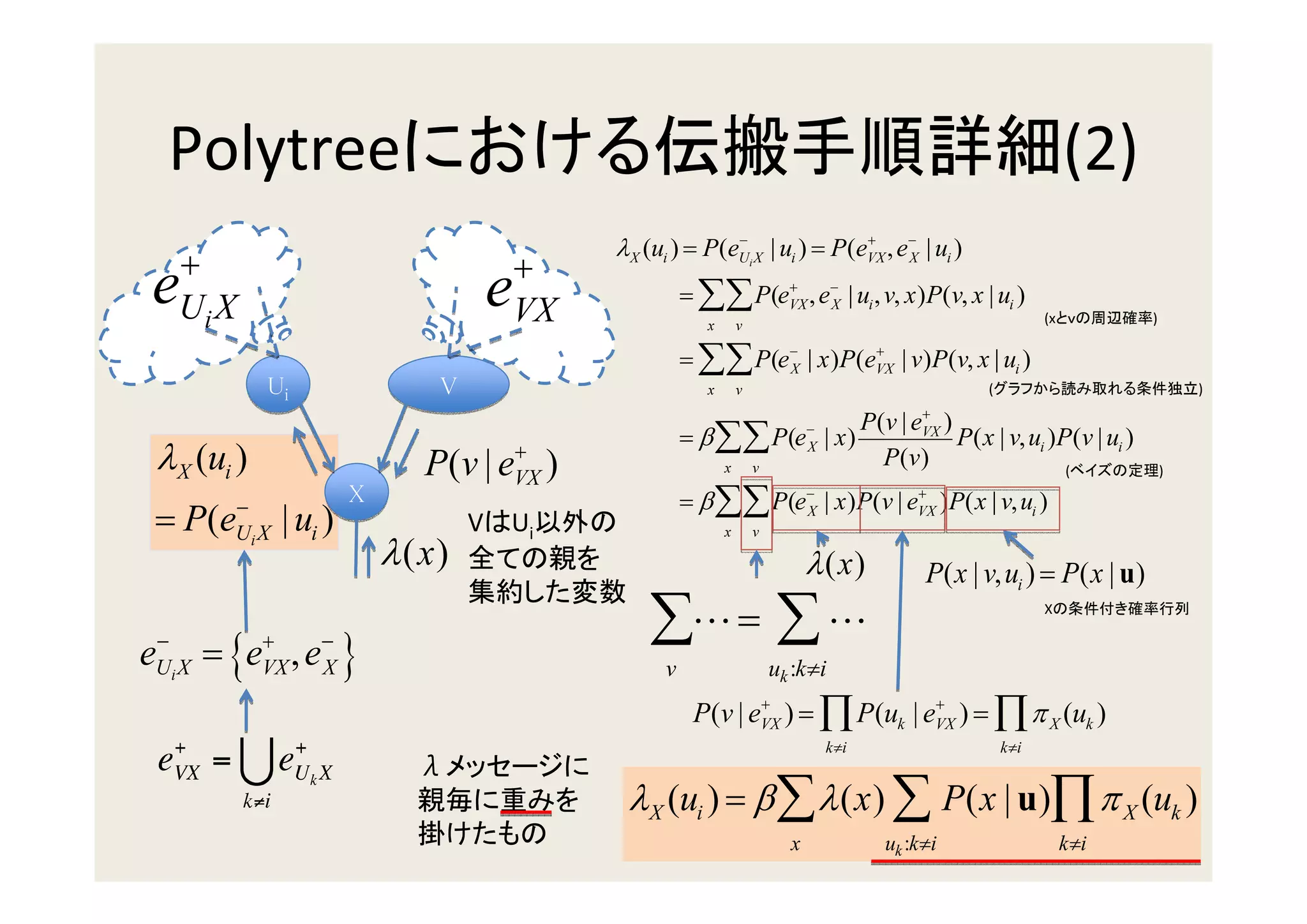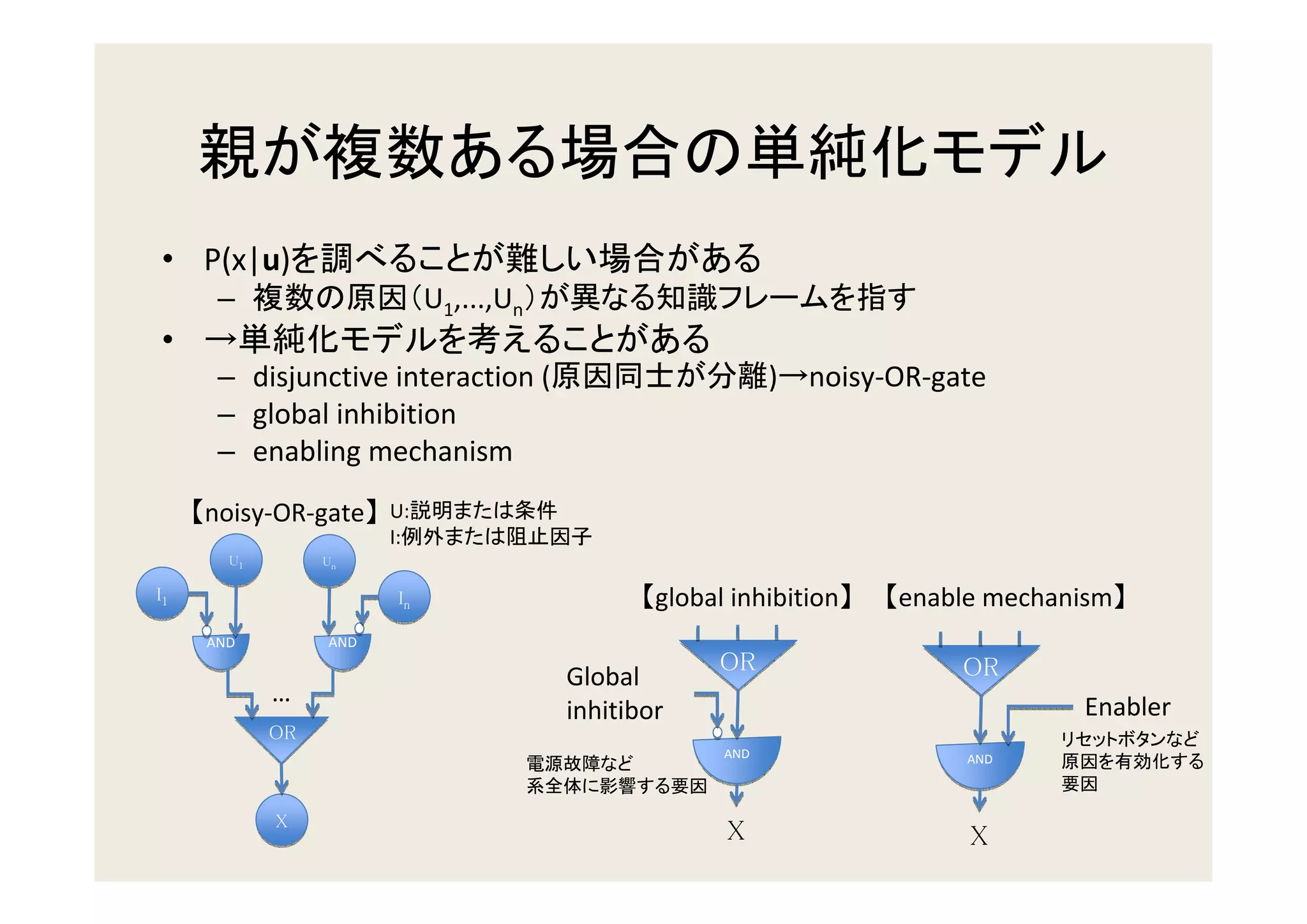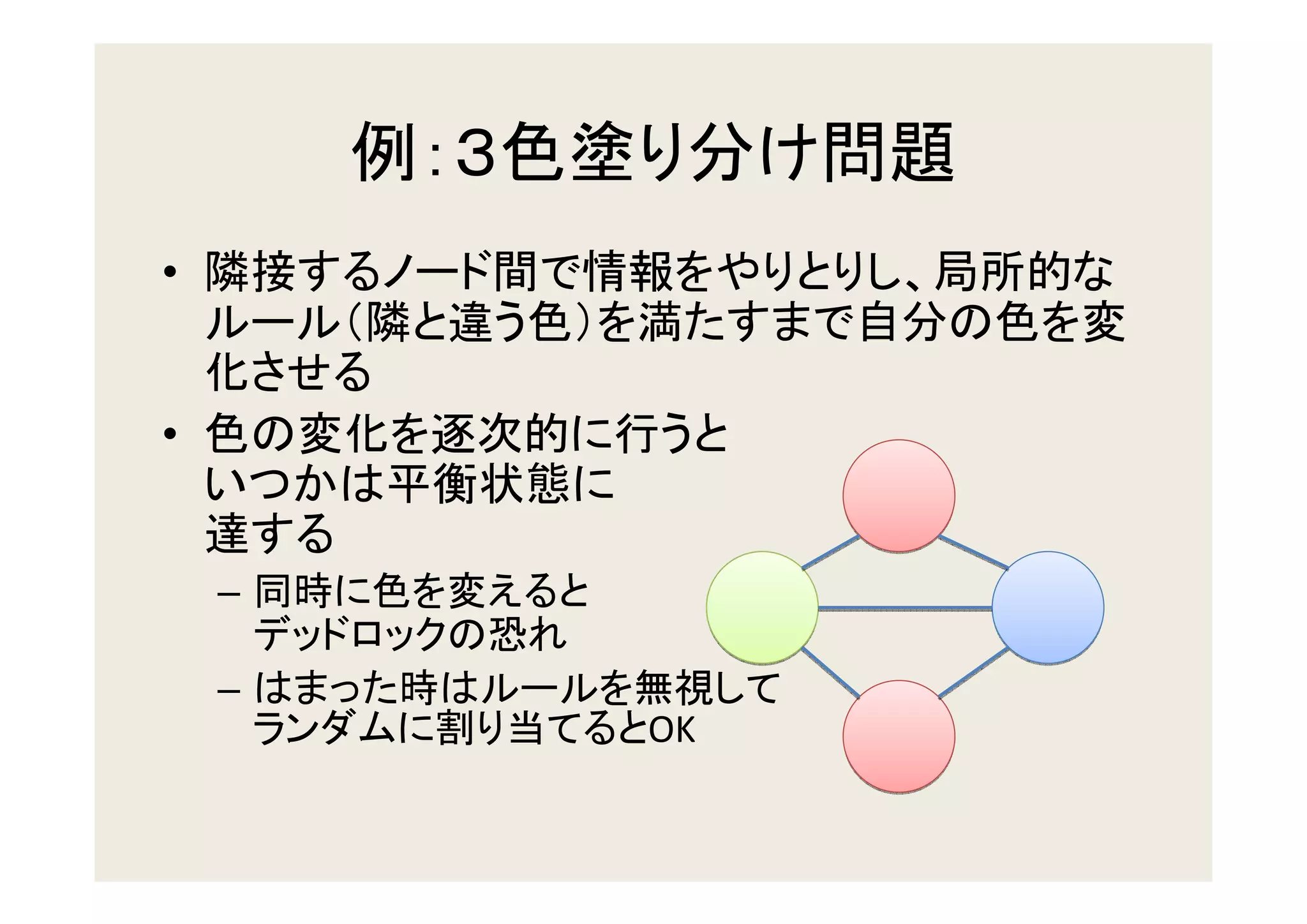3. Updating beliefs in chains, trees, and polytrees by propagating probabilities along the edges of the graph structure.

1. Chapter 4
BELIEF UPDATING BY NETWORK
PROPAGATION
Probabilistic Reasoning In Intelligent
Systems.

2. •
– 4.1
• - -
– 4.2.1
– 4.2.2
– 4.2.3
– 4.3 (Polytrees)

4. 1.
i.
ii.
2.
1.i.

5. P(xi , x j )
∑ P(x , x i j | xk )
xk ∈X k
P(xi | x j ) = =
P(x j ) P(x j ) Xi
• ( Xk)
•
– Xk
–
•
–
Xj
–
–

6. •
•
→
=1?

7. •
•
–
–
OK

8. •
–
•
–
–

9. • N1 N1
–
– N1
•
–
t2 t3
→
…
→

11. M y|x ≡ P(y | x) ≡ P(Y = y | X = x)
y
x P(y1 | x1 ) P(y2 | x1 ) L P(yn | x1 ) 
 
 P(y1 | x2 ) P(y2 | x2 ) L P(yn | x2 ) 
= 
 M M O M 
 P(y1 | xm ) P(y2 | xm )
 L P(yn | xm ) 

+: ¬: / +a:A ¬a:A
e
X BEL(x) ≡ P(x|e)
f(x) λ(x)
f(x)g(x) / (1,2,3)(3,2,1)=(1x3,2x2,3x1)=(3,4,3)
f(x) g(x) / (1,2,3) (3,2,1) = 1x3+2x2+3x1 = 10
( ) f (x)• M ≡ f (x)M y|x ∑ y|x
x
α ( 1 )
β
1 = (1,1,1,1)

12. X 3x3
3 
 0.80 if x = y x, y = 1, 2, 3
M y|x = P(y | x) = 
 0.10 if x ≠ y x, y = 1, 2, 3

Y
∑ P(z | y) = 1 for y = 1, 2, 3
z
Z virtual
P(z |y=1):P(z |y=2): P(z |y=3)=8:6:5
MYCIN • unity( 1)
•

13. 2 chain
X Y
e={Y=y}
X P(x) My|x X→Y
λ(x)=P(e|x)
BEL(x)=P(x|e) =P(Y=y|x)
=αP(x)P(e|x) ∵ =My|x (0,...,1,...,0)
=αP(x)λ(x) Y=y
=[P(e)]-1P(x)λ(x) ※ y
 P(y | x )L P(Y = y | x ) LP(y | x ) 
 1 1 1 n 1

 M M M 
 P(y | x )L P(Y = y | x ) P(y | x ) 

 1 m m n m 


14. 3 chain
X Y Z
λ(y)=P(Z=z|y)
e={Z=z}
BEL(x)=P(x|e) P(x) λ (x) = P(e | x) My|x
=Mz|y Mz|y
=αP(x)λ(x)
=[P(e)]-1P(x)λ(x) = ∑ P(e | y, x)P(y | x)
←x y
y
= ∑ P(e | y)P(y | x) ←I(X,Y,Z)
y
= M y|x • λ (y)  P(y | x ) L P(y | x )   λ (y ) 
 1 1 n 1
  1

M y|x • λ (y) =  M O M  • M 
 P(y | x ) L P(y | x )   λ (y ) 

 1 m n m  
  n 

 P(y | x )λ (y ) +L+ P(y | x )λ (y ) 
 1 1 1 n 1 n

= M 
 P(y | x )λ (y ) +L+ P(y | x )λ (y ) 

 1 m 1 n m n 


15. Mu|t Mx|u My|x Mz|y
P(t) T U X Y Z … Evidence e
λ(t) λ(u) λ(x) λ(y) λ(z)
• λ
λ
• λ Evidence e

16. e+ T U X Y Z e-
π (x) = P(x | e+ ) π(x)=P(x|e+) BEL(x) λ(x)=P(e-|x)
= ∑ P(x | u, e+ )P(u | e+ ) ≡P(x|e+,e-)
u =αP(e-|x,e+)P(x|e+)
= ∑ P(x | u)π (u) =αP(e-|x)P(x|e+)
u =αλ(x)π(x)
= π (u)• M x|u
• π(x) λ(x)
• π(x)

17. X
π(u) π(x)
π(x)
Mx|u
BEL(x)
My|x
λ( )
λ( ) λ(y)
X
π(u) π(x)
π(x)
Mx|u
BEL(x)
Mx|u
λ( )
λ(u) λ(x)
λ

18. U
BEL(x)=P(x|e X ,e X )=αP(eX |x)P(x|eX )=αλ ( x)π ( x),
+ - - +
λX(u) πX(u)
V W
λ(x) = P(eX |x)=P(eY ,eZ |x)=P(eY |x)P(eZ |x)=λY (x)λZ (x),
- - - - -
X
λY(x) λZ(x)
π(x) = P(x|eX )=∑ P(x|eX ,u)P(u|eX ) = ∑ P(x|u)P(u|eX )
+ + + +
u u
πY(x) πZ(x)
Y Z = ∑ P(x|u)π X (u) = M x|u • π X (u),
u
∴ BEL(x) = αλY (x)λZ (x)∑ P(x|u)π X (u).
u
• X (V,U,W) e+ U
• chain
– X root λ
– π

19. λX(u) πX(u)
X
M λ π M
λ(x) π(x)
π j (x) = π Y (x) = P(x | eY )
j
+
j
= P(x | e+ , eY1,L)
X
−
∏λ ( x) α(λπ)
= α ∏ P(eYk | x)P(x | eX )
k
k − +
k≠ j
BEL(x)
 
BEL(x)
= α  ∏ λYk (x) π (x)
 
α
 k≠ j 
BEL(x)
α
λ1 (x) λ2 (x)
BEL(x)
λ1(x) λ2(x) π1(x) π2(x) =α
λ j (x)

20. Polytree(
U1 U2 ... Un − +
1 2 n
BEL( x) = αP(e X | x) P( x | e X ) = αλ ( x)π ( x).
−
{
Let e X = e − XY1 ,K, e − XYm } {
e + X = e + U1 X , K , e + U n X , }
X m
λ ( x ) ≡ P (e −
X | x ) = P (e −
XY2 ,K, e −
XYm | x) = ∏ λY j ( x),
j =1
Y1 Y2 ... Ym
Let π X (ui ) = P(ui | e +U i X ).
π ( x) ≡ P ( x | e +U X , K , e +U X )
1 n
• = ∑ P( x | u ,K, u ) P(u ,K, u
u1 ,K,u n
1 n 1 n | e + U1 X , K , e + U n X )
n
= ∑ P( x | u)∏ π X (ui ) ※
X Y u i =1
 m  n

BEL( x) = α ∏ λY j ( x) ∑ P( x | u)∏ π X (ui )
Z=z  j =1  u i =1 

21. Polytree
• Polytree
• 3
1. π (causal support)
2. λ (diagnostic support)
3. P(x|u1,...,un): (conditional-probability matrix)
• 3step
1. Belief-updating U1 U2 ... Un
X π λ P(x|u1,...,un) BEL(x)=αλ(x)π(x)
2. Bottom-up propagation
X λ λ
X
3. Top-down propagation
X π π
• ( ...
Y1 Y2 Ym
1.
π(x) P(x)
2.
λ(x) = (1,1,…,1)
3.
λ(x) = δx,x’ =(0,...,1,...,0) : x’ 1
X Z Z→X λ δx,x’

22. Polytree (1)
1. Belief-updating
X π λ P(x|u1,...,un) BEL(x)=αλ(x)π(x)
λ ( x) = ∏ λY ( x),π ( x) =
j
j ∑
u1 ,K,u n
P( x | u1 ,K, un )∏ π X (ui ),
i
2. Bottom-up propagation
X λ λ
λX (ui ) = β ∑ λ ( x) ∑ P( x | u1 ,K, un )∏ π X (uk ) ※tree
x u k :k ≠ i k ≠i (2)
3. Top-down propagation
X π π
  BEL( x)
π Y j ( x j ) = α ∏ λYk ( x) ∑ P( x | u1 ,K, un )∏ π X (ui ) = α .
 k≠ j  u1 ,K,un i λY j ( x)

23. Polytree (2)
λX (ui ) = P(eU X | ui ) = P(eVX , e− | ui )
− +
+ + i X
e Ui X e VX
= ∑∑ P(eVX , e− | ui , v, x)P(v, x | ui )
x
+
v
X
(x )
= ∑∑ P(e− | x)P(eVX | v)P(v, x | ui )
X
+
Ui V x v ( )
+
P(v | eVX )
= β ∑∑ P(e | x) −
P(x | v, ui )P(v | ui )
λX (ui ) +
P(v | eVX ) x v P(v)
X
( )
−
X = β ∑∑ P(e− | x)P(v | eVX )P(x | v, ui )
+
= P(e Ui X | ui ) V Ui x
X
v
λ (x) λ (x) P(x | v, ui ) = P(x | u)
eUi X = {eVX , e− }
− + ∑L = ∑L X
X v uk :k≠i
P(v | eVX ) = ∏ P(uk | eVX ) = ∏ π X (uk )
+ +
k≠i k≠i
λ
λX (ui ) = β ∑ λ (x) ∑ P(x | u)∏ π X (uk )
x uk :k≠i k≠i

24. • P(x|u)
– U1,...,Un
• →
– disjunctive interaction ( )→noisy-OR-gate
– global inhibition
– enabling mechanism
noisy-OR-gate U:
I:
U1
U1 U
U
I1
1 In
n global inhibition enable mechanism
AND AND
OR OR
Global
…
inhitibor Enabler
OR
AND
AND AND
AND
X
X X