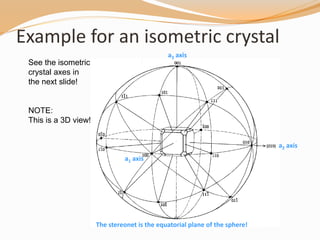
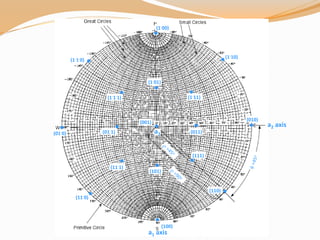
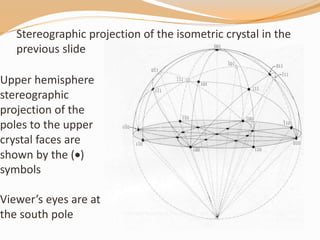
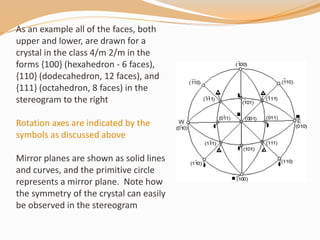
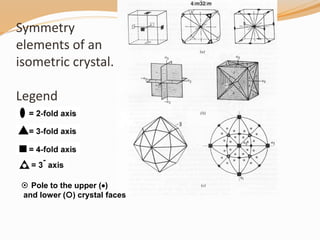
This document provides an overview of stereographic projection as it relates to crystals. It discusses how stereographic projection preserves the 3D angular relationships of crystals in a 2D representation. It covers the key aspects of stereographic projection including the two main types of stereonets (Wulff and Schmidt), how to project lines, planes, and symmetry elements, and the conventions and steps to plot crystallographic data. Examples are provided to demonstrate how to plot poles to faces and measure angles on a stereonet for both isometric and general crystals.

1. Dr. Harisingh Gour Vishwavidyalaya, Sagar
(A Central university)
Presentation
On
Stereographic projection of crystals
Anshul Sahu
(M.Tech I year 2018-19)
Submitted to
Prof. R.K Trivedi

2. Content
 Introduction
 Types of stereonet
 Projection of line
 Projection of plane
 Mirror and polygon symbol
 Convention
 Rules
 Examples.

3. Introduction
 Crystals have a set of 3D geometric relationships
among their planar and linear features
 These include the angle between crystal faces, normal
(pole) to these faces, and the line of intersection of these
faces
 Planar features: crystal faces, mirror planes
 Linear features: pole to crystal faces, zone axis, crystal
axes

4. Stereographic Projection
 Projection of 3D orientation data and symmetry
of a crystal into 2D by preserving all the angular
relationships
 First introduced by F.E Neuman and further
developed by W.H Miller
 In mineralogy, it involves projection of faces,
edges, mirror planes, and rotation axes onto a
flat equatorial plane of a sphere, in correct
angular relationships

5. Two Types of Stereonet
 Wulff net (Equal angle)
 Used in mineralogy when angles are meant to be
preserved.
 e.g., for crystallography and core analysis
 Projection is done onto both the upper and
lower hemispheres
 Schmidt net (Equal area)
 Used in structural geology for orientation
analysis when area is meant to be preserved for
statistical analysis
 Uses projection onto the lower hemisphere

6. Wulff net for
Minerals 
-90
0
+90
-135
+135



7. Wulff Stereonet (equal angle net)
 Shows the projection of great circles and small circles
 Great circle: Line of intersection of a plane, that passes
through the center of the sphere, with the surface of the
sphere (like lines of longitude on Earth)
 NOTE: Angular relationships between points can only
be measured on great circles (not along small circles)!
 Small circle: Loci of all positions of a point on the surface
of the sphere when rotated about an axis such as the
North pole (like lines of latitude on Earth)

8. Stereographic projection of a line
• Each line (e.g., rotation axis, pole to a mirror plane) goes
through the center of the stereonet .
• The line intersects the sphere along the ‘spherical projection
of the line’, which is a point
• A ray, originating from this point, to the eyes of a viewer
located vertically above the center of the net (point O),
intersect the ‘primitive’ along one point
• The point is the stereographic projection of the line.
• A vertical line plots at the center of the net
• A horizontal line plots on the primitive

9. Special cases of lines
 Vertical lines (e.g., rotation axes, edges) plot at the
center of the equatorial plane
 Horizontal lines plot on the primitive
 Inclined lines plot between the primitive and the
center

10. Projection of Planar Elements
 Crystals have faces and mirror planes which are
planes, so they intersect the surface of the sphere
along lines
 These elements can be represented either as:
 Planes, which become great circle after projection
 Poles (normals) to the planes, which become
points after projection

11. Stereographic projection of a plane:
• Each plane (e.g., mirror plane) goes through the
center of the stereonet (i.e., the thumbtack)
• The plane intersects the sphere along the
‘spherical projection of the plane’, which is a
series of points
• Rays, originating from these points, to the eyes
of a viewer located vertically above the center of
the net (point O), intersect the ‘primitive’ along a
great circle
• The great circle is the stereographic projection of
the plane. The great circle for a:
• vertical plane goes through the center
• horizontal plane parallels the primitive

12. Special cases of planes
 Stereographic projection of a horizontal face or mirror
plane is along the primitive (perimeter) of the equatorial
plane
 Stereographic projection of a vertical face or mirror plane
is along the straight diameters of the equatorial plane
 They pass through the center
 They are straight ‘great circles’
 Inclined faces and mirror planes plot along curved great
circles that do not pass through the center

13. 12
3
Face 3
 pole to the
crystal face
Face 1: vertical
Face 2: inclined
Face 3: horizontal

14. Preparing to plot
 Mark N of the net as -90, E as 0, S as =+90 )(for ).
 Mount the stereonet on a cardboard. Laminate it. Pass
a thumbtack through the center from behind the board
 Secure the thumbtack with a masking tape from behind
the cardboard
 Place a sheet of tracing paper on the stereonet
 Put a scotch tape at the center, from both sides of the
tracing paper; pierce the paper through the pin
 Tracing paper can now rotate around the thumbtack
without enlarging the hole (because of scotch tape)

15. Symbols used
 For faces below the equator (when using lower hemisphere), place an
open circle symbol () where the ray connecting the spherical
projection of the pole to the plane intersects the equatorial plane
 This is the stereographic projection of the pole to the face
 For faces above the equator (when using the upper hemisphere),
place a solid circle symbol ( ) the ray connecting the spherical
projection of the pole to the plane intersects the equatorial plane
 Use a bull’s-eye symbol () to show a point above the page that
coincides with one directly below it (when using both hemispheres)
 Reorient the stereogram such that lines of symmetry are north-
south or east-west


16. Mirror and Polygon Symbols
 To plot symmetry axes on the stereonet, use the
following symbol conventions:
Mirror plane: ― (solid line great circles)
Crystal axes (lines):

18. Measuring angle between faces
 This is done using the poles to the faces!
 Three cases:
1. On the primitive, the angle is read directly on the
circumference of the net
2. On a straight diameter, the paper is rotated until the
zone is coincident with the vertical diameter (i.e., N-S or
E-W) and the angle measured on the diameter
3. On a great circle (an inclined zone), rotate the paper
until the zone coincides with a great circle on the net;
read the angle along the great circle

19. Convention
 By convention (Klein and Hurlbut, p.62), we place the
crystal at the center of the sphere such that the:
 c-axis (normal of face 001) is the vertical axis
 b-axis (normal of face 010) is east-west
 a-axis (normal of face 100) is north-south
 See next slide!

20. axis
axis
a axis
E-W
Up and down
N-S
Stereonet is
the equator

21. The ρ angle
 The ρ angle, is between the c axis and the pole to the
crystal face, measured downward from the North pole of
the sphere
 A crystal face has a ρ angle measured in the vertical plane
containing the axis of the sphere and the face pole.
 Note: the (010) face has a ρ angle of 90o
 (010) face is perpendicular to the b-axis
 The φ angle is measured in the horizontal equatorial plane.
 Note: the (010) face has a φ angle of 0o!

22. Plotting ρ and φ
Suppose you measured ρ = 60o and φ = 30o for a face with goniometer.
Plot the pole to this face on the stereonet.
Procedure: Line up the N of the tracing paper with the N of the net.
From E, count 30 clockwise, put an x (or a tick mark). Bring x to the E,
and then count 60 from the center toward E, along the E-W line. Mark
the point with .
NOTE: The origin for the φ angle is at E (i.e., φ =0).
-φ is counted counterclockwise, horizontally from E to the N on the primitive.
+φ is counted clockwise horizontally from E to S (i.e., clockwise) on the primitive.

23. Example for an isometric crystal
See the isometric
crystal axes in
the next slide!
NOTE:
This is a 3D view!
a2 axis
a1 axis
a3 axis
The stereonet is the equatorial plane of the sphere!

24. a2 axis
a1 axis
(011)
(1-11)
(111)
(001)
(101)
(11-1)
(01-1)
(1-1-1)
(1-01)
(1-10)


 
 


(010)
(1-00)






(11-0)
(1-1-0)
(01-0)
(110)
(100)
a3

25. Upper hemisphere
stereographic
projection of the
poles to the upper
crystal faces are
shown by the ()
symbols
Viewer’s eyes are at
the south pole
Stereographic projection of the isometric crystal in the
previous slide

26. • In the previous slide, only the upper faces of an isometric
crystal are plotted. These faces belong to forms {100}, {110},
and {111}
• Form: set of identical faces related by the rotational
symmetry (shown by poles/dots in stereograms)
• Faces (111) and (110) both have a φ angle of 45o
• The ρ angle for these faces is measured along a line from the
center of the stereonet (where the (001) face plots) toward
the primitive. For the (111) face the ρ angle is 45o, and for the
(110) face the ρ angle is 90o
Explanation of Previous Slide

27. As an example all of the faces, both
upper and lower, are drawn for a
crystal in the class 4/m 2/m in the
forms {100} (hexahedron - 6 faces),
{110} (dodecahedron, 12 faces), and
{111} (octahedron, 8 faces) in the
stereogram to the right
Rotation axes are indicated by the
symbols as discussed above
Mirror planes are shown as solid lines
and curves, and the primitive circle
represents a mirror plane. Note how
the symmetry of the crystal can easily
be observed in the stereogram

28. Symmetry
elements of an
isometric crystal.
Legend
 Pole to the upper ()
and lower () crystal faces

29. The following rules are applied:
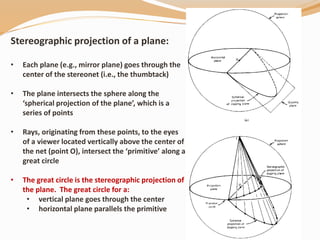
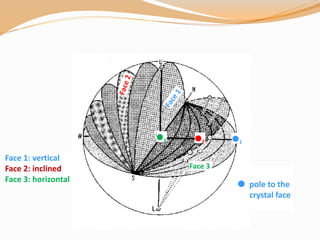
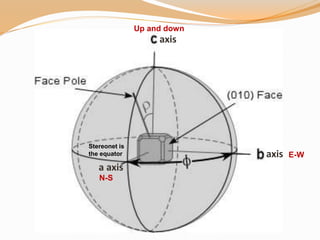
 All crystal faces are plotted as poles (lines perpendicular to the
crystal face. Thus, angles between crystal faces are really
angles between poles to crystal faces
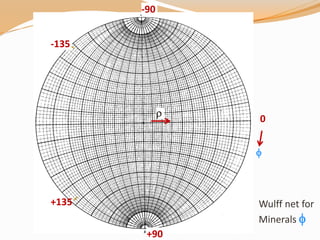
 The b crystallographic axis is taken as the starting point. Such
an axis will be perpendicular to the (010) crystal face in any
crystal system. The [010] axis (note the zone symbol) or (010)
crystal face will therefore plot at φ = 0o and ρ = 90o
 Positive φ angles will be measured clockwise on the stereonet,
and negative φ angles will be measured counter-clockwise on
the stereonet

30. Rules cont’d
 Crystal faces that are on the top of the crystal (ρ < 90o) will be
plotted with the closed circles () symbol, and crystal faces on
the bottom of the crystal (ρ > 90o) will be plotted with the ""
symbol
 Place a sheet of tracing paper on the stereonet and trace the
outermost great circle. Make a reference mark on the right
side of the circle (East)
 To plot a face, first measure the φ angle along the outermost
great circle, and make a mark on your tracing paper. Next
rotate the tracing paper so that the mark lies at the end of the
E-W axis of the stereonet

31. Stereographic Projection
 References:
 Dexter Perkins, 2002, Mineralogy, 2nd edition.
Prentice Hall, New Jersey, 483 p.
 Bloss, F.D., 1971, Crystallography and Crystal
Chemistry: Holt, Reinhardt, and Winston, New
York, 545 p.

32. Thank you