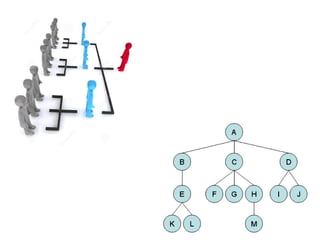
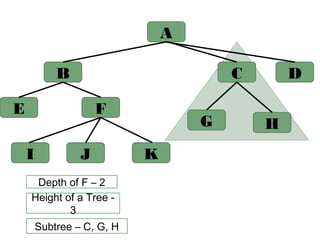
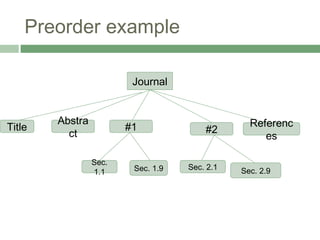
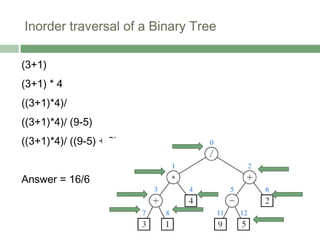
The document discusses trees as a non-linear data structure that organizes elements hierarchically through parent-child relationships. It provides terminology and key concepts related to tree structure, traversal algorithms, and binary trees, including methods for accessing and manipulating tree nodes. It also covers binary search trees and their properties, emphasizing their applications in representing arithmetic expressions and decision processes.

1. Algorithms and Data Structures
Week 5
TREES – Non linear data structure
By – Priyanka Rana

2. Do you have a non linear mind?

3. Breakthroughs come by thinking "nonlinearly“.

4. Data Structure - Trees
 Non linear.
 Faster than linear data structures.

5. Applications

8. Trees
 Is an abstract data type.
 Defined as a set of nodes that stores elements
hierarchically.
 Consists of nodes with a
parent- child relation.

9. Parent-child relationship

10. Tree terminology
 Root
 If tree T is nonempty, it has a special node, called the
root of T, that has no parent.
 Internal Node
 Node with at least one child.
 External Node (leaf)
 Node without children.

11. Tree terminology
 Siblings
 Nodes that are children of the same parent.
 Ancestors of a Node
 Parent, grandparent, grand-grandparent.
 Descendants of a Node
 Child, grand child, grand-grandchild etc.

12. Tree terminology
 Edge
 An edge of tree T is a pair of nodes (u, v) such
that u is the parent of v, or vice versa.
 Path
 Path of T is a sequence of nodes such that any
two consecutive nodes in the sequence form an
edge.

13. A
DCB
E F
I J K
G H
ROOT - A
Internal Node- A, B, F,
C
External Node- E, I, J, K, G,
H, D
Sibling of B – C,D
Ancestors of F - A, B,
Descendant of B - E, I, J, K, F
Path – A, B, F, K

14. Tree terminology
 Ordered Trees
If there is a linear ordering defined for the children of each
node, visualized by arranging siblings left to right.
Book
Prefac
e
Part A Part B
Referenc
es
Ch. 5 Ch.
6
^ ^ ^ ^
Sec.
1.1 Sec. 1.9
Ch.
1
Sec. 10.1 Sec. 10.9
Ch.
10

15. Tree Abstract Data Type
 positions in a tree are its nodes.
 position object for a tree supports the method:
position <E> element()
Return the object stored at this position.

16. Tree’s accessors methods
 position root():
 Return the tree’s root.
 position parent(p):
 Return the parent of p.
 Iterable children(p):
 Return an iterable collection containing the children of node
p.

17. Tree’s query methods
 boolean isInternal(p):
 Test whether node P is internal.
 boolean isExternal(p):
 Test whether node p is external.
 boolean isRoot(p):
 Test whether node p is the root

18. Tree’s generic methods
 int size()
 Return the number of nodes in the tree.
 boolean isEmpty()
 Indicates whether the tree has any nodes.
 iterator iterator()
 Return an iterator of all elements stored at nodes of the tree.
 iterable position()
 Return an iterable collection of all the nodes of the tree.
 element replace(v, e)
 Replace with e and return the element stored at node v.

19. A
DCB
E F
I J K
G H
Size() - 11
isInternal(A) -
True
isExternal(E) - True
isRoot(C) - False isEmpty - False

20. Method Running Time
Size, isEmpty() O(1)
iterator, positions O(n)
Replace O(1)
Root, parent O(1)
isExternal O(1)
isInternal O(1)
isRoot O(1)

21. Tree traversal Algorithms
 A traversal of a Tree T is a systematic way of
accessing(or visiting) all the nodes of T.

22.  How can we index node?
 Position
 public Iterable <Position<E>> positions();
 How can we index children of node?
 Iterable
 public Iterator<E> iterator();

23. Tree ADT
 Depth of a node
 number of ancestors.
 Height of a tree
 maximum depth of any node.
 Subtree
 tree consisting of a node and its descendants.

24. Algorithm depth(T, v):
if v is the root of T then
return 0
else
return 1 + depth(T,w)

25. Algorithm height(T)
h0
for each vertex v in T do
if v is an external node in T then
h max (h, depth(T,v))
return h

26. A
DCB
E F
I J K
G H
Depth of F – 2
Height of a Tree -
3
Subtree – C, G, H

27. Traversal schemes
 preorder traversal
 Node is visited before its descendants.
 Children of each node of an ordered tree are
ordered from left to right.
 postorder traversal
 Node is visited after its descendants.
 Children of each node of an ordered tree are
ordered from left to right.

28. Preorder traversal
 Algorithm preorder(T, v):
visit(v);
for each child w of v do
preorder(T, w);
 Application
 print a structured document
 Running Time
 O(n)

29. Preorder example
Journal
Abstra
ct
#1 #2
Referenc
es
Sec.
1.1 Sec. 1.9 Sec. 2.1 Sec. 2.9
Title

30. Postorder traversal
 Algorithm postorder(T, v):
– for each child w of v do
– postorder(T, w);
– visit(v);
 Application
 computer space used by files in a directory and its subdirectories.
 Running Time
 O(n)

31. Postorder example
CP2410
Tutorial
Lectur
es
Week 10
Subject Outline
Tut 1 Tut 10 Week 1 Week 5

32. Exercise
What is the output of preorder and postorder
traversal of this tree?

33. What’s special about this tree?

34. Binary Trees
A binary tree is an ordered tree :
 Every node has at most two children.
 Each child node is labelled as being either a left child or
a right child.
 A left child precedes a right child in the
ordering of children of a node.

35. Binary trees Application
 A binary tree is proper or full
 If each node has either zero or two children.
 Application
 Representation of arithmetic expressions
 Internal nodes : operators
 External nodes : operands

36. Arithmetic expression tree
(2 x (a -1) + (3 x
b))
2
a 1
3 b
+
-
x x

37. Binary trees Application
 Representation of decision process
 Internal nodes : questions with yes/no answer
 External nodes : decisions

38. Binary Tree ADT - Accessor methods
 position left(p):
 Return the left child of p.
 position right(p):
 Return the right child of p.
 boolean hasLeft(p):
 Test whether p has a left child.
 boolean hasRight(p):
 Test whether p has a right child.

39. Binary Tree Implementation
 Linked Lists

40. Binary Tree Implementation
........ .... .
.
A B D G H
Array
If v is the root of T, then p(v) = 1.
If v is the left child of node u, then p(v) = 2p(u).
If v is the right child of node u, then p(v) = 2p(u)

41. Inorder traversal of a Binary Tree
Algorithm inorder(T, v):
if v has a left child u in T then
inorder(T, u) {recursively traverse left subtree}
perform the “visit action for node v
if v has a right child w in T then
inorder(T, w) {recursively traverse right subtree}

42. Inorder traversal of a Binary Tree
(3+1)
(3+1) * 4
((3+1)*4)/
((3+1)*4)/ (9-5)
((3+1)*4)/ ((9-5) + 2)
Answer = 16/6

43. Binary search
 x(v) – element stored in any internal node.
 For each internal node v of T:
 The elements stored in the left subtree of v are less than or
equal to x(v).
 The elements stored in the right subtree of v are greater
than or equal to x(v).
 The external nodes of T do not store any element.

44. Binary search tree
The blue solid path is traversed when searching (successfully) for 36.
The blue dashed path is traversed when searching (unsuccessfully)
for 70.