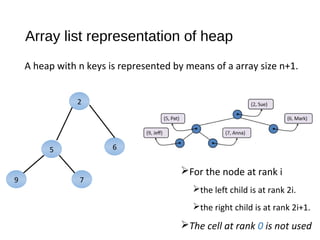
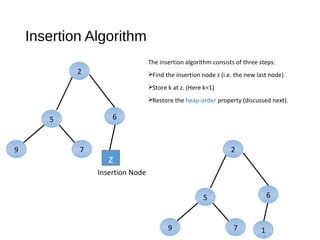
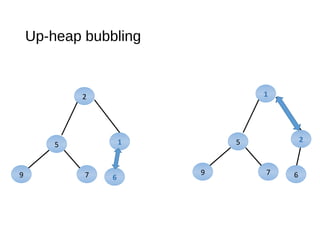
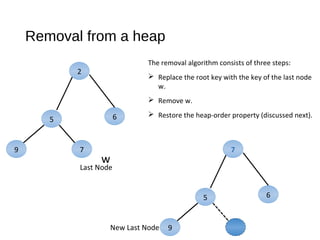
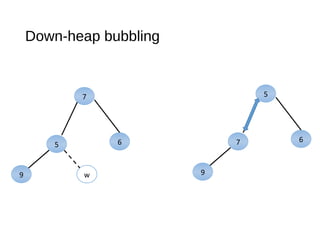
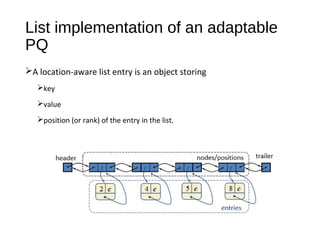
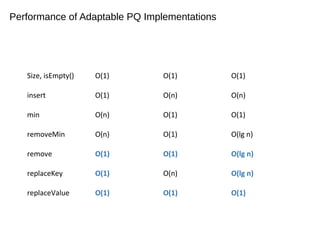
The document discusses heaps and adaptable priority queues, outlining their properties, operations, and performance across various implementations, including unsorted lists, sorted lists, and heaps. It details the insertion and removal algorithms, the structure of a heap as a binary tree, and how heap-sort operates within a time complexity of O(n log n). Additionally, it introduces adaptable priority queues used in specific applications, emphasizing their functionalities and efficiency in managing priority queue entries.

1. Heaps & Adaptable Priority
Queues
By – Priyanka Rana

2. Session 2 review
In list-based implementation of priority queue:
If we use unsorted lists:
 insertion takes O(1) time
 deletion takes O(n) time.
If we use sorted lists:
 insertion takes O(n) time
 deletion takes O(1) time.

3. Session 2 Review
Selection-sort:
Phase 1 -> fast running time.
Phase 2 -> slow running time.
Insertion-sort:
Phase 1 -> slow running time.
Phase 2 -> fast running time.

4. Balancing the running time
Heap

5. Heap Data structure
Is a binary tree T that stores a collection of entries at its nodes
and satisfies two additional properties:
Order Property
Structure Property

6. Heap properties
Order Property:
For every internal node v, other than the root, key(v) ≥
key(parent(v)).
Structure Property:
A heap T with height h is a complete binary tree, i.e.:
for depth/level i < h, there are 2i nodes.
at depth h−1, the internal nodes are to the left of the external
nodes.

7. Heap data structure
The last node of a heap is the rightmost node of the
maximum depth.
2
65
89 Last node

8. Height of heap
A heap storing n keys has height h = [lg n]
For each depth i < h , there are 2i nodes and
at least one node at depth h. Thus,
n ≥ 20 + 21+ 22 + ... + 2h-1 + 1
≥ 1 + 2 + 4 + ... + 2h-1 + 1
≥ 2h
Which gives, h ≤ lgn.

9. Array list representation of heap
For the node at rank i
the left child is at rank 2i.
the right child is at rank 2i+1.
The cell at rank 0 is not used
A heap with n keys is represented by means of a array size n+1.
2
65
79
0 1 2 3 4 5
2 5 6 79

10. Insertion Algorithm
The insertion algorithm consists of three steps:
Find the insertion node z (i.e. the new last node).
Store k at z. (Here k=1)
Restore the heap-order property (discussed next).
2
65
79 2
5
79
z
Insertion Node
6
1

11. Up-heap bubbling
1
5
79
2
6
2
5
79
1
6

12. Removal from a heap
The removal algorithm consists of three steps:
 Replace the root key with the key of the last node
w.
 Remove w.
 Restore the heap-order property (discussed next).
2
65
79 7
5
9
w
Last Node
6
New Last Node

13. Down-heap bubbling
5
7
9
6
7
5
w9
6

14. Heap-sort
A heap-based priority queue, sorts a sequence of n
elements in O(nlgn) time.
performs n series of removeMin() operation.
Since each call of removeMin() takes O(lgn) time, sorting a
heap with n elements takes O(nlgn) time.

15. Merging two heaps
2
6
3
8 5
72
47
4

16. Exercise
At which nodes of a heap can an entry with the
largest key be stored?

17. Adaptable Priority Queues
Priority queues which are adaptable.
When priority queue methods are not sufficient.
For example, in a standby airline passenger application.

18. Adaptable Priority Queue ADT
remove(e):
Remove from P and return e.
replaceKey(e, k):
Replace with k and return the key of entry e of P.
replaceValue(e, x):
 Replace with x and return the value of entry e of P.

19. Exercise
Operation Output
Insert(5,A) e1
Insert(3,B) e2
Insert(7,C) e3
min() e2
Key(e2) 3
remove(e1) e1
replaceKey(e2,9) 3
replaceValue(e3,D
)
C
Remove(e2) e2
isEmpty() “false”
(3,B)
,
(5,A),(7,C),(9,B),(7,D)

20. Location aware entry
mechanism for finding the position of entry e of Priority Queue P.
This position is called the location of the entry
implementation of an entry that keeps track of its position is called
location-aware entry.

21. List implementation of an adaptable
PQ
A location-aware list entry is an object storing
key
value
position (or rank) of the entry in the list.

22. Heap Implementation of an Adaptable PQ
A location-aware list entry is an object storing
key
value
position of the entry in the heap.

23. Performance of Adaptable PQ Implementations
Method Unsorted List Sorted List Heap
Size, isEmpty() O(1) O(1) O(1)
insert O(1) O(n) O(n)
min O(n) O(1) O(1)
removeMin O(n) O(1) O(lg n)
remove O(1) O(1) O(lg n)
replaceKey O(1) O(n) O(lg n)
replaceValue O(1) O(1) O(1)

24. THANK YOU