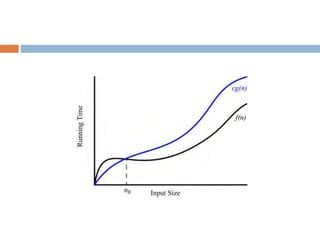
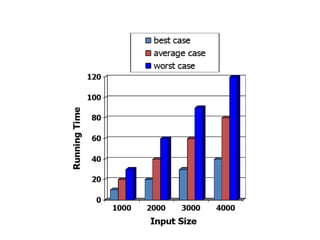
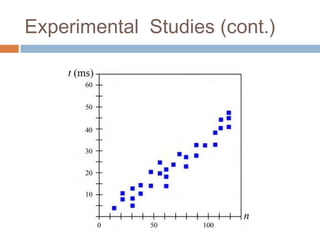
The document covers seven functions and the analysis of algorithms, including constant, logarithmic, linear, n-log-n, quadratic, cubic, and exponential functions. It describes the process of experimental studies for algorithm analysis, detailing steps, limitations, and examples such as the arraymax algorithm. Additionally, it explains asymptotic notation, including big-oh, big-omega, and big-theta notations, providing definitions and examples for each.

1. Algorithms and Data Structures
Algorithm analysis
By- Priyanka

2. Session 4 is about
 Seven Functions
 Analysis of algorithms

3. 1. Constant Function
Simplest function:
f(n) = c (some fixed constant)
Value of n doesn’t matter.
Ex: adding two numbers, assigning variable,
comparing two numbers

4. 2. Logarithm Function
f (n) = logb n
for some constant b > 1
This function is defined:
x = logbn if and only if bx = n
Value b is known as the base of the logarithm.
log n = log2 n.

5. Rules for algorithms
Given real numbers a , c > 0, and b , d > 1, we have
If b = 2, we either use log n, or lg n.

6. 3. Linear function
f(n) = c n
Function arises when a single basic
operation is required for each of n
elements.

7. 4. N- log- N function
f(n) = n logn
Grows faster than the linear function.
Slower than the quadratic function.

8. 5. Quadratic function
f(n) = n2
For nested loops, where combined operations of
inner and outer loop gives n*n = n2.

9. 6. Cubic Function & Other Polynomials
f(n) = n3
Comparatively less frequent

10. 7. Exponential Function
f(n) = bn
b is a positive constant, called as the base.
n is the argument and called as the exponent.
Also called as exponent function.

11. Analysis of algorithm
Analysis of algorithm means:
Predicting the amount of resources
that the algorithm requires.

13. Analysis of algorithms
 Experimental Studies
 Primitive Operations
 Asymptotic Notation

14. Experimental Studies
Running time of implemented algorithm is calculated
by:
 Executing it on various test inputs.
 Recording the actual time spent in each
execution.
 Using the System.curent Time Millis () method.

15. Experimental Studies (cont.)
Steps :
1. Write a program implementing the algorithm.
2. Run the program with inputs of varying size and
composition.
3. Use a system call to get running time measure.
4. Plot the results.
5. Perform a statistical analysis.

16. Experimental Studies (cont.)

17. Limitations of Experimental analysis
 Need limited set of test inputs.
 Need same hardware and software
environments.
 have to fully implement and execute an
algorithm.

18. Primitive operations
Set of primitive operations:
1. Assigning a value to a variable.
2. Calling a method.
3. Performing an arithmetic operation (for example, adding two numbers).
4. Comparing two numbers.
5. Indexing into an array.
6. Following an object reference.
7. Returning from a method.

19. Example
Algorithm arrayMax(A, n)
# operations
currentMax ← A[0] 2
for i ← 1 to n − 1 do 2n
if A[i] > currentMax then 2(n − 1)
currentMax ← A[i] 2(n − 1)
{ increment counter i } 2(n − 1)
return currentMax 1
Total 8n − 2

20. Estimating Running Time
 Algorithm arrayMax executes 8n − 2 primitive
operations in the worst case.
 Define:
a = Time taken by the fastest primitive operation
b = Time taken by the slowest primitive operation
 Let T(n) be worst-case time of arrayMax. Then
a (8n − 2) ≤ T(n) ≤ b(8n − 2)
 Hence, the running time T(n) is bounded by two
linear functions.

21. Asymptotic Notation
 Uses mathematical notation for functions.
 Disregards constant factors.
 n refer to a chosen measure of the input “size”.
 Focus attention on the primary "big-picture"
aspects in a running time function.

22. Asymptotic Notation(cont.)
 Big-Oh Notation
 Big-Omega Notation
 Big-Theta Notation

23. Big – Oh Notation
Given functions are f(n) and g(n)
f(n) is O(g(n)) if there are positive constants
c>0 and n0 ≥1 such that
f(n) ≤ cg(n) for n ≥ n0

24. Big – Oh Notation (cont.)
Example: 2n + 10 is O(n)
2n + 10 ≤ cn
(c − 2) n ≥ 10
n ≥ 10/(c − 2)
Pick c = 3 and n0 = 10

25. Big – Oh Notation (cont.)
 Example: the function n2 is not O(n)
n2 ≤ cn
n ≤ c
The above inequality cannot be satisfied since c
must be a constant

27. Big – Omega Notation
Given functions are f(n) and g(n)
f(n) is Ω(g(n)) if there are positive constants
c>0 and n0 ≥1 such that
f(n) ≥ cg(n) for n ≥ n0

28. Big – Omega Notation(cont.)
Example : the function 5n2 is Ω(n2)
5n2 ≥ c n2
5n ≥ c n
c = 5 and n0 = 1

29. Big – Theta Notation
Given functions are f(n) and g(n)
f(n) is Θ(g(n)) if f(n) is O(g(n)) and f(n) is Ω(g(n)) ,
that is, there are real constants
c’> 0 and c’’ >0 and n0 ≥1 such that
c’ g(n) ≤ f(n) ≤ c’’ g(n) for n ≥ n0

30. Big – Theta Notation(cont.)
 Example : 3nlog n + 4n + 5logn is Θ(n log
n).
Justification:
3nlogn ≤ 3nlogn + 4n + 5logn ≤
(3+4+5)nlog n
for n ≥ 2

31. Thank You