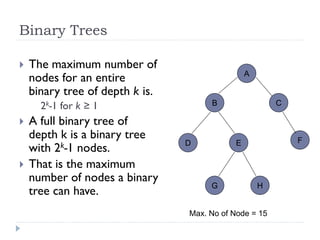
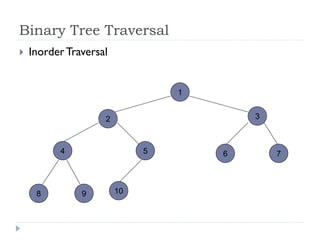
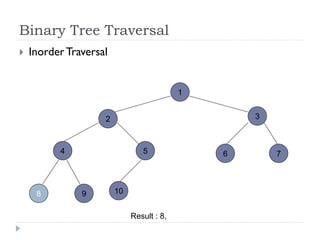
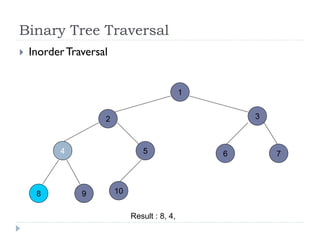
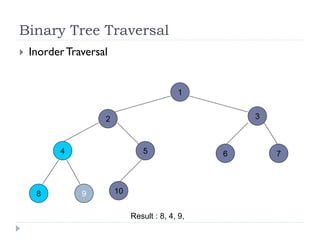
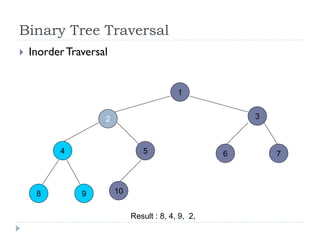
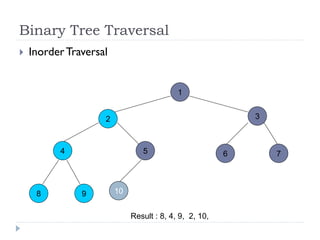
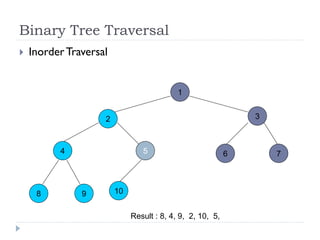
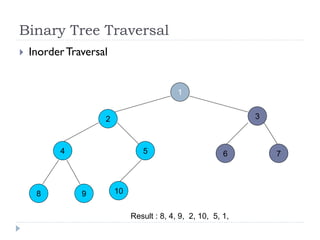
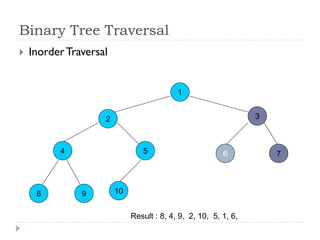
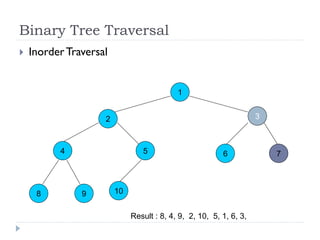
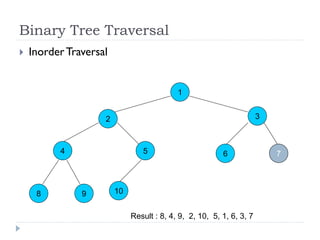
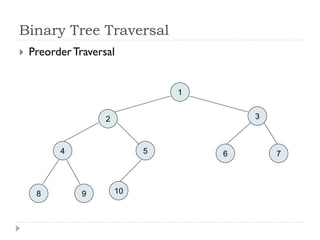
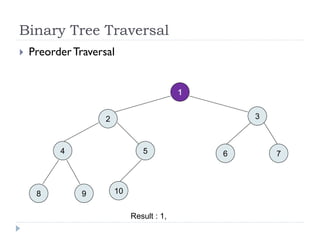
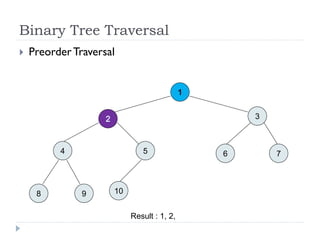
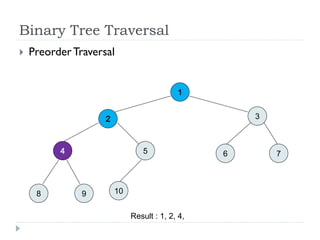
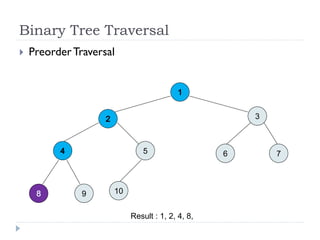
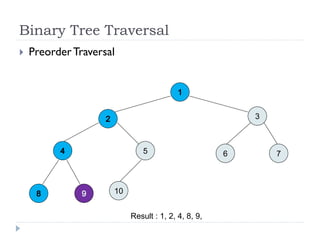
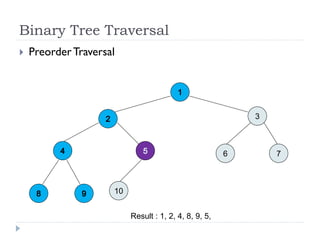
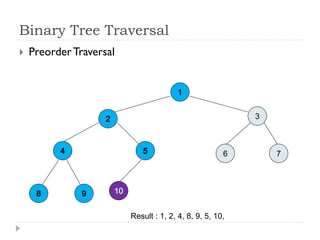
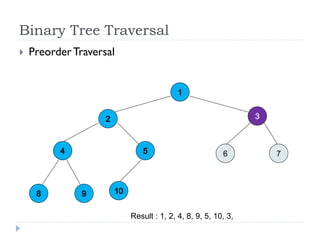
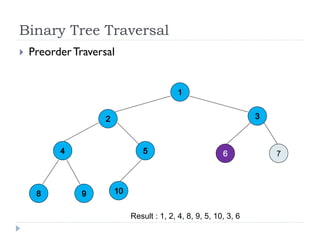
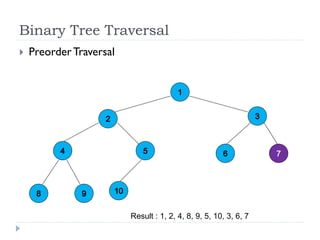
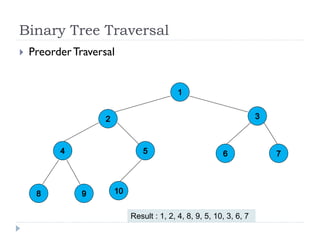
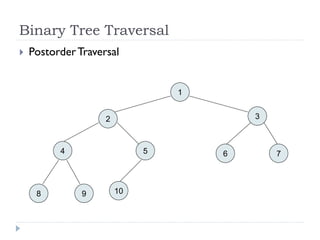
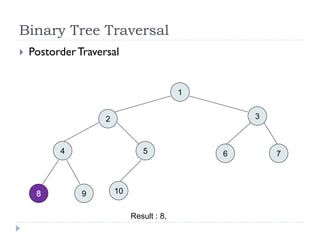
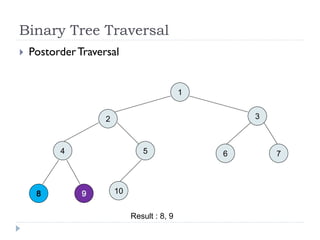
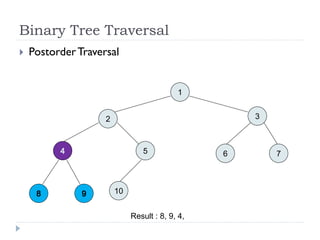
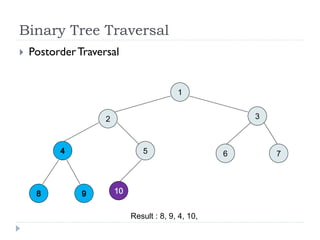
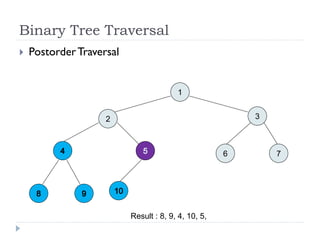
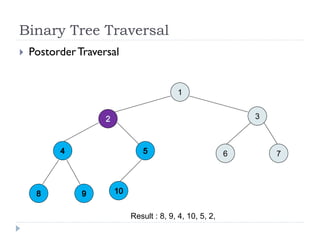
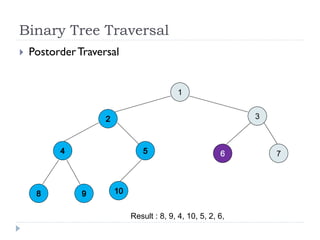
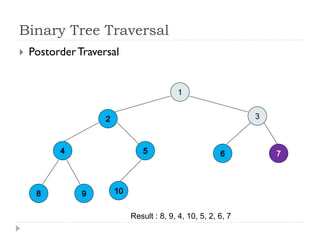
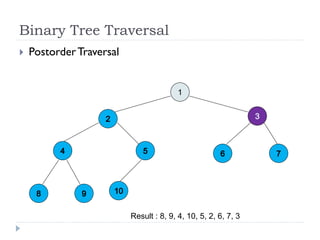
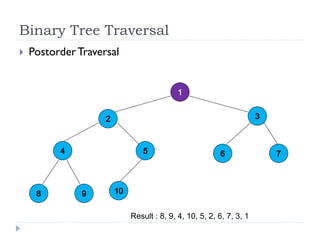
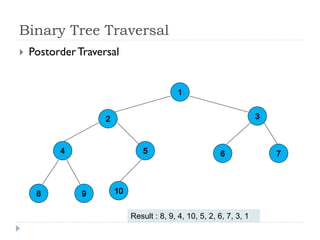
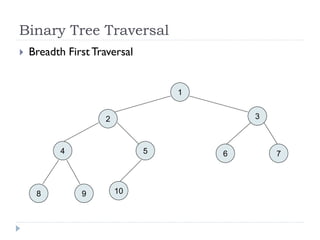
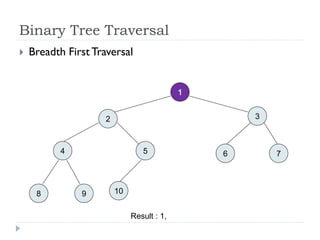
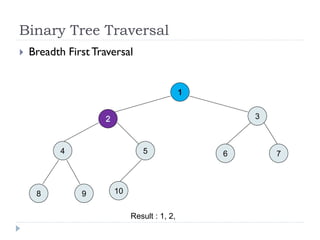
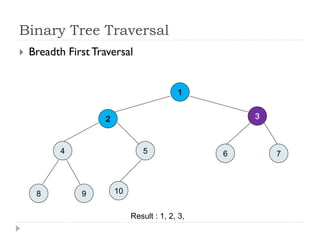
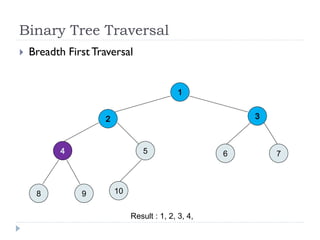
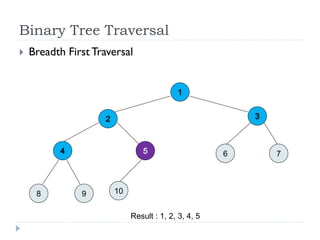
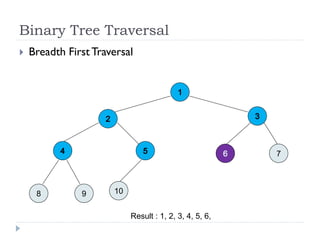
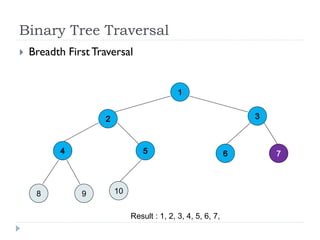
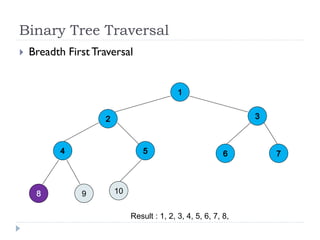
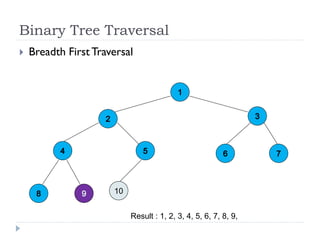
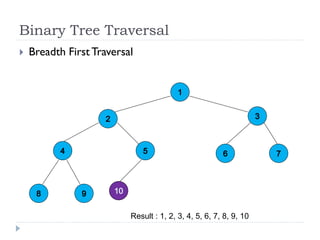
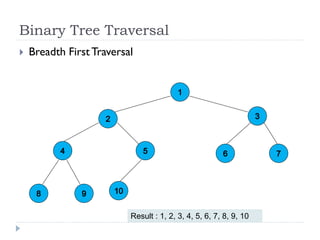
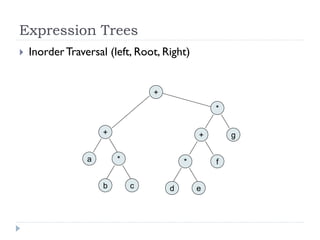
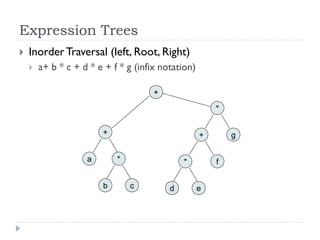
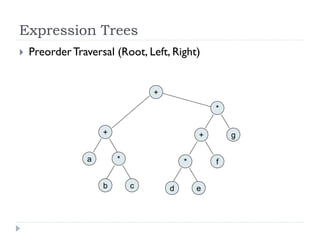
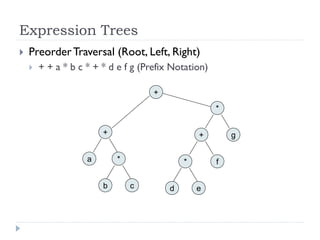
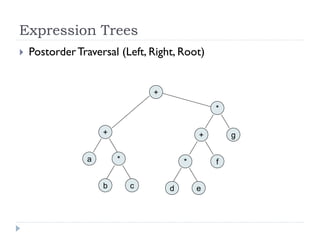
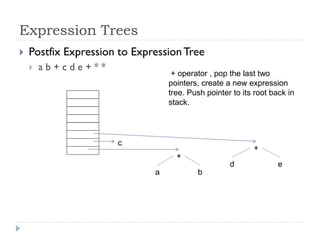
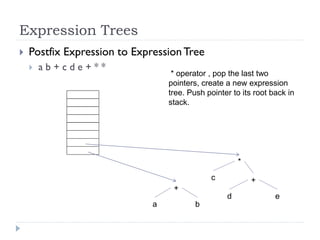
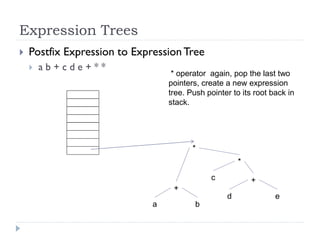
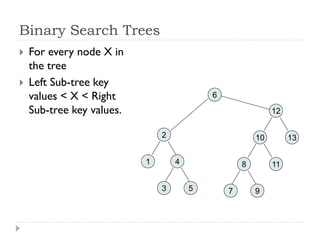
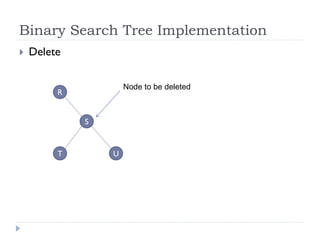
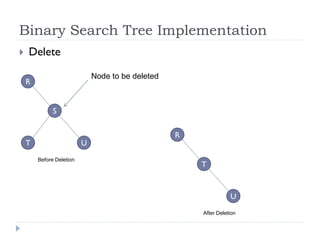
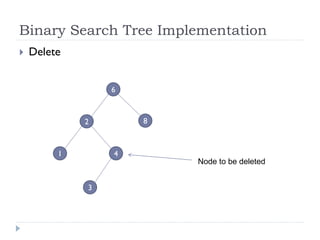
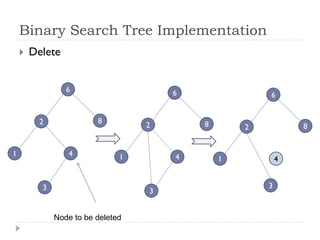
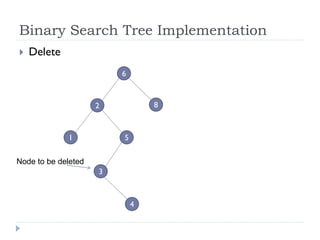
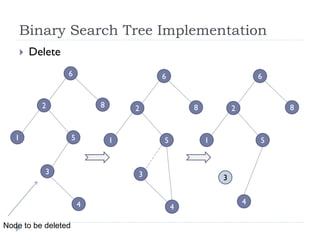
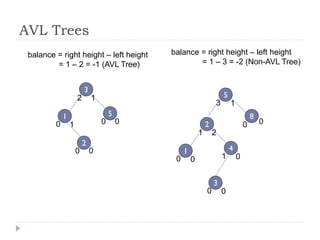
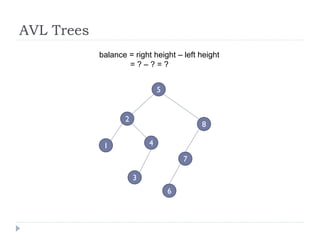
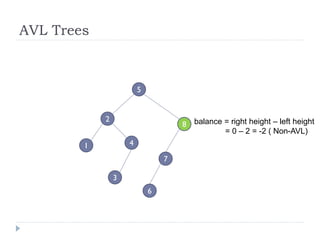
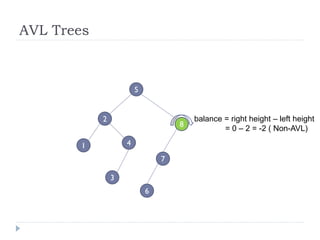
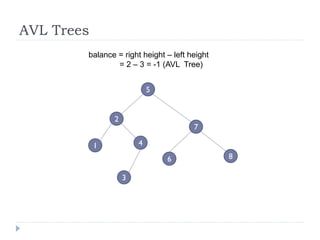
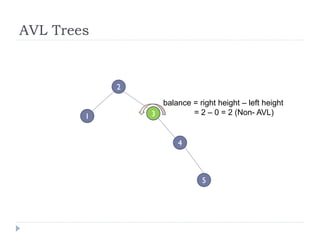
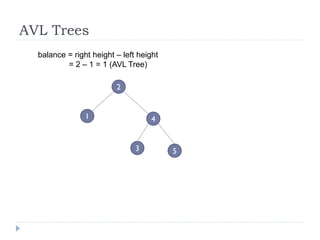
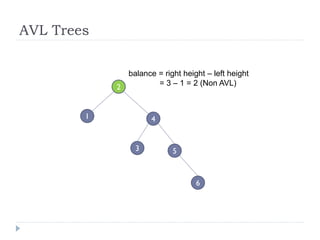
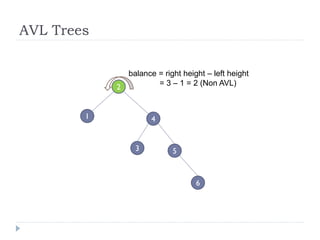
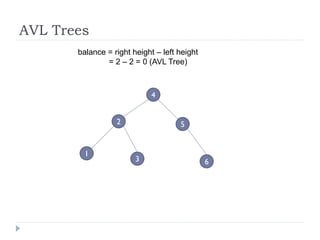
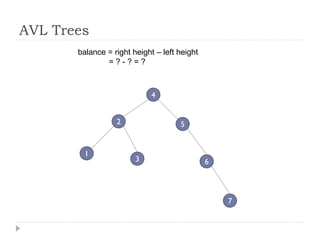
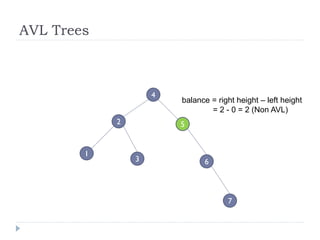
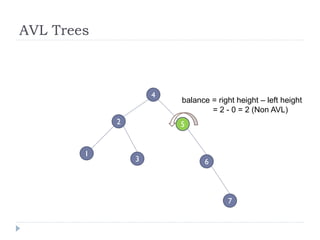
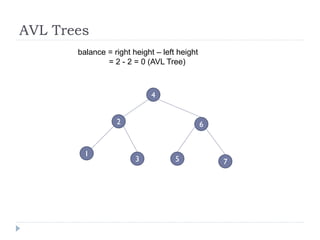
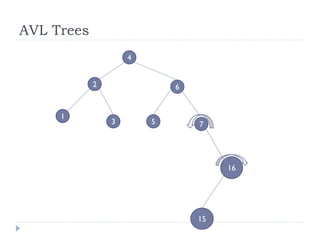
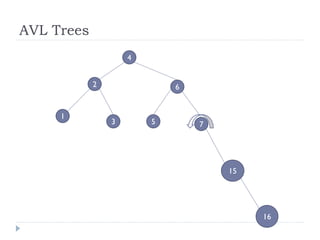
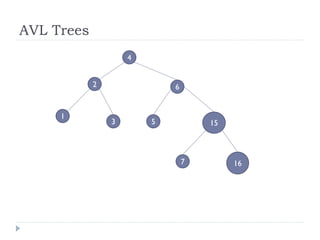
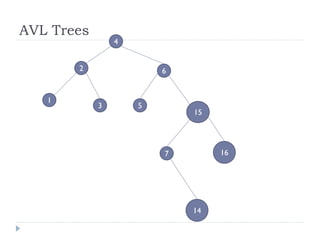
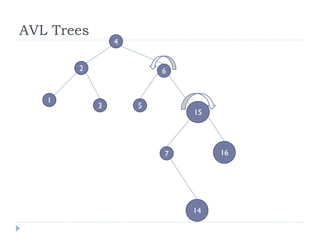
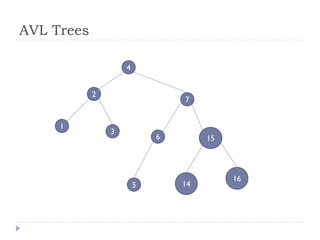
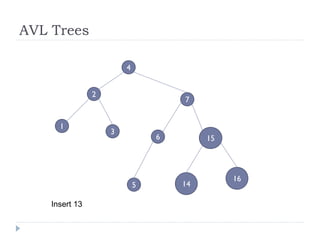
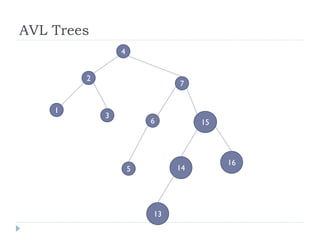
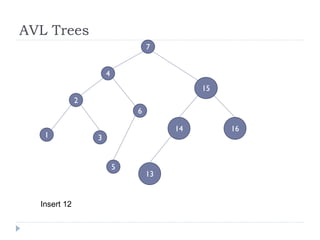
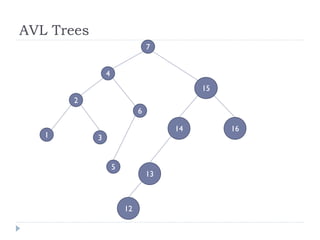
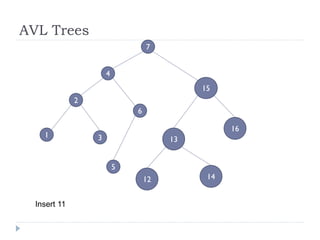
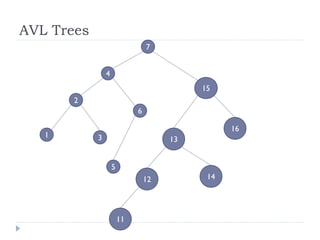
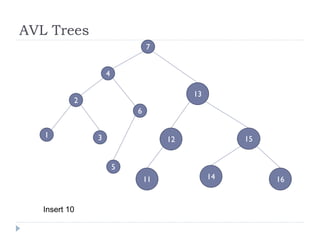
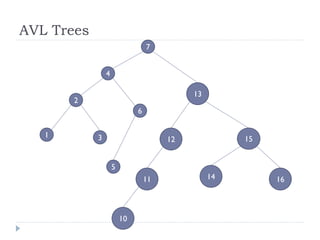
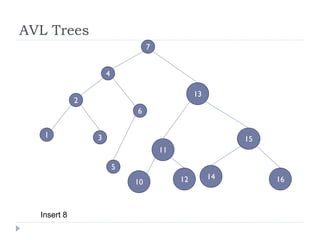
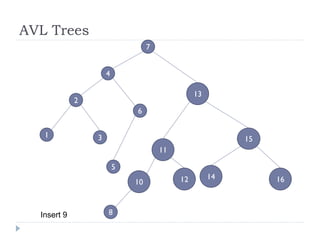
The document discusses binary trees and their implementation and traversal methods. It defines a binary tree as a tree where each node has at most two children. It describes the common traversal orders of binary trees as inorder, preorder and postorder. It also discusses breadth first traversal and storing binary trees using node structures. Expression trees are described as binary trees used to represent mathematical expressions where leaves are operands and internal nodes are operators.