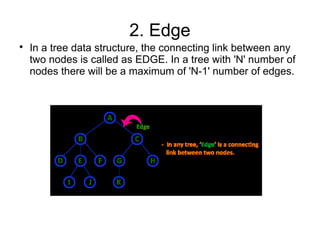
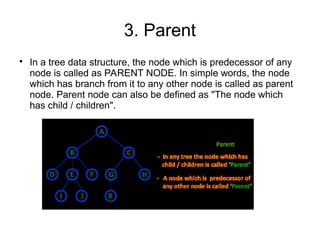
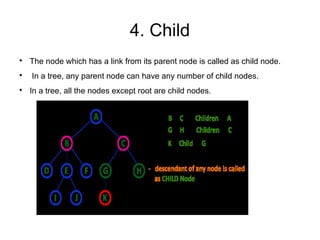
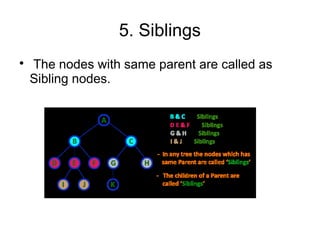
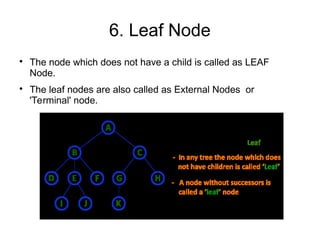
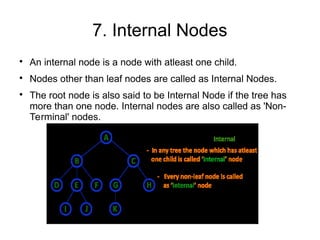
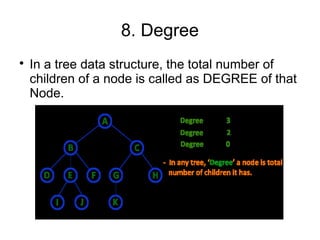
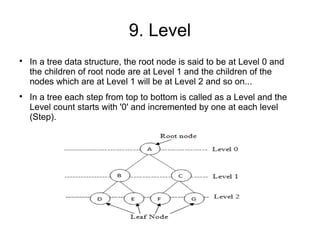
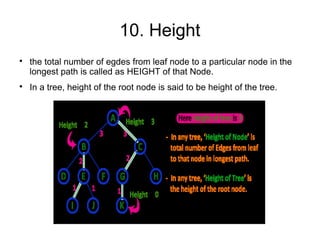
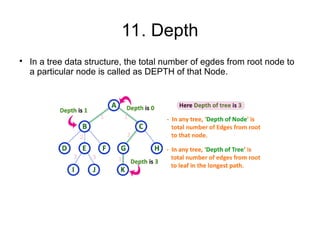
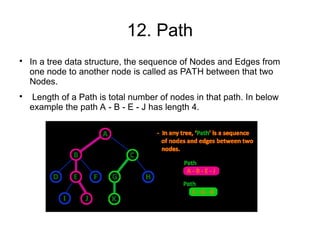
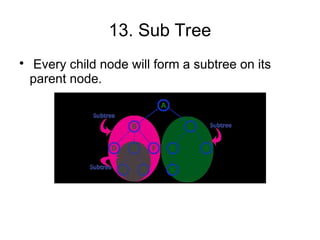
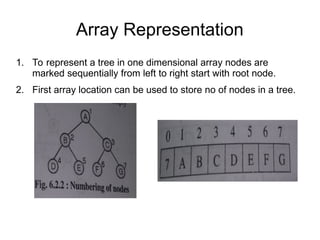
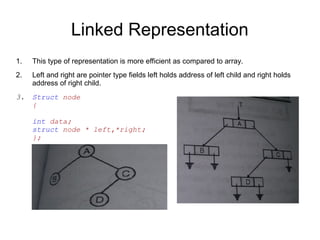
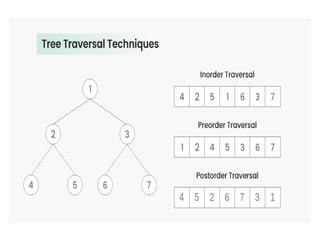
The document provides an overview of tree data structures, explaining their hierarchical organization and key terminology such as root, edge, parent, child, and various types of trees including binary trees and expression trees. It also details tree traversal methods such as preorder, inorder, and postorder, along with representations in arrays and linked lists. Additionally, the document highlights binary search trees and their properties, emphasizing the importance of organization and traversal in data management.

1. Tree: Non Linear Data
Structures
By: Bijoyeta Roy

2. Trees: Non-Linear data structure
A data structure is said to be linear if its elements form a sequence or a
linear list. Previous linear data structures that we have studied like an array,
stacks, queues and linked lists organize data in linear order.
A data structure is said to be non linear if its elements form a hierarchical
classification where, data items appear at various levels.
Trees and Graphs are widely used non-linear data structures. Tree and
graph structures represent hierarchical relationship between individual data
elements. Graphs are nothing but trees with certain restrictions removed.

3. Tree Definition
Tree is a non-linear data structure which organizes
data in hierarchical structure and this is a
recursive definition.

4. A tree data structure can also be defined as follows...
A tree is a finite set of one or more nodes such
that:
There is a specially designated node called the
root. The remaining nodes are partitioned into
n>=0 disjoint sets T1, ..., Tn, where each of
these sets is a tree. We call T1, ..., Tn are the
subtrees of the root.

5. Tree terminology...

1.Root:
 The first node is called as Root Node.
 Every tree must have root node, there must be
only one root node.
 Root node doesn't have any parent.

6. 2. Edge

In a tree data structure, the connecting link between any
two nodes is called as EDGE. In a tree with 'N' number of
nodes there will be a maximum of 'N-1' number of edges.

7. 3. Parent

In a tree data structure, the node which is predecessor of any
node is called as PARENT NODE. In simple words, the node
which has branch from it to any other node is called as parent
node. Parent node can also be defined as "The node which
has child / children".

8. 4. Child

The node which has a link from its parent node is called as child node.

In a tree, any parent node can have any number of child nodes.

In a tree, all the nodes except root are child nodes.

9. 5. Siblings

The nodes with same parent are called as
Sibling nodes.

10. 6. Leaf Node

The node which does not have a child is called as LEAF
Node.

The leaf nodes are also called as External Nodes or
'Terminal' node.

11. 7. Internal Nodes

An internal node is a node with atleast one child.

Nodes other than leaf nodes are called as Internal Nodes.

The root node is also said to be Internal Node if the tree has
more than one node. Internal nodes are also called as 'Non-
Terminal' nodes.

12. 8. Degree

In a tree data structure, the total number of
children of a node is called as DEGREE of that
Node.

13. 9. Level

In a tree data structure, the root node is said to be at Level 0 and
the children of root node are at Level 1 and the children of the
nodes which are at Level 1 will be at Level 2 and so on...

In a tree each step from top to bottom is called as a Level and the
Level count starts with '0' and incremented by one at each level
(Step).

14. 10. Height

the total number of egdes from leaf node to a particular node in the
longest path is called as HEIGHT of that Node.

In a tree, height of the root node is said to be height of the tree.

15. 11. Depth

In a tree data structure, the total number of egdes from root node to
a particular node is called as DEPTH of that Node.

16. 12. Path

In a tree data structure, the sequence of Nodes and Edges from
one node to another node is called as PATH between that two
Nodes.

Length of a Path is total number of nodes in that path. In below
example the path A - B - E - J has length 4.

17. 13. Sub Tree

Every child node will form a subtree on its
parent node.

18. Type of Trees
• General tree
• Binary tree
• Binary Search Tree

19. General Tree
• A general tree is a data structure in that each node can have infinite number of children .
• In general tree, root has in-degree 0 and maximum out-degree n.
• Height of a general tree is the length of longest path from root to the leaf of tree. Height(T)
= {max(height(child1) , height(child2) , … height(child-n) ) +1}
•

20. Binary tree
• A Binary tree is a data structure in that each node has at most two
nodes left and right
• In binary tree, root has in-degree 0 and maximum out-degree 2.
• In binary tree, each node have in-degree one and maximum out-
degree 2.
• Height of a binary tree is : Height(T) = { max (Height(Left Child) ,
Height(Right Child) + 1}

21. Representation of Binary Tree
1. Array Representation
2. Linked List Representation.

22. Representation of Binary Tree
Struct node
{
int data;
struct node * left,right;
};

23. Array Representation
1. To represent a tree in one dimensional array nodes are
marked sequentially from left to right start with root node.
2. First array location can be used to store no of nodes in a tree.

24. Linked Representation
1. This type of representation is more efficient as compared to array.
2. Left and right are pointer type fields left holds address of left child and right holds
address of right child.
3. Struct node
{
int data;
struct node * left,*right;
};

25. Binary Tree Types
1. Complete Binary Tree
2. Full Binary Tree
3. Skewed Binary Tree
4. Strictly Binary Tree
5. Expression Binary tree

26. Complete Binary Tree
A complete binary tree is a tree in which
1. All leaf nodes are at n or n-1 level
2. Levels are filled from left to right
A complete binary tree is a binary tree in which every level,
except possibly the last, is completely filled, and all nodes in
the last level are as far left as possible.

27. Full Binary Tree
A full binary tree is a binary tree in which all of the nodes
have either 0 or 2 offspring. In other terms, a full binary
tree is a binary tree in which all nodes, except the leaf
nodes, have two offspring. Also known as strict binary
tree
No of nodes= 2h
-1

28. Skewed Binary Tree
A binary tree is said to be Skewed Binary Tree if every node in the
tree contains either only left or only right sub tree. If the node
contains only left sub tree then it is called left-skewed binary
tree and if the tree contains only right sub tree then it is
called right-skewed binary tree.

29. Expression Binary tree
• Expression trees are a special kind of binary tree used to
evaluate certain expressions.
• Two common types of expressions that a binary expression
tree can represent are algebraic and boolean.
• These trees can represent expressions that contain both unary
and binary operators.
• The leaves of a binary expression tree are operands, such as
constants or variable names, and the other nodes contain
operators.
• Expression tree are used in most compilers.

31. Binary Tree Traversal
1. Preorder traversal:-In this traversal method
first process root element, then left sub tree
and then right sub tree.
Procedure:-
Step 1: Visit root node
Step 2: Visit left sub tree in preorder
Step 3: Visit right sub tree in preorder

32. 2. Inorder traversal:-
In this traversal method first process left element,
then root element and then the right element.
Procedure:-
Step 1: Visit left sub tree in inorder
Step 2: Visit root node
Step 3: Visit right sub tree in inorder

33. 3. Post order traversal:-
In this traversal first visit / process left sub tree,
then right sub tree and then the root element.
Procedure:-
Step 1: Visit left sub tree in post order
Step 2: Visit right sub tree in post order
Step 3: Visit root node

35. PREORDER-{30 , 20 , 15 , 5 , 18 , 25 , 40 , 35 , 50 , 45 , 60}
POST ORDER- {5 , 18 , 15 , 25 , 20 , 35 , 45 , 60 , 50 , 40 , 30}
IN ORDER is {5 , 15 , 18 , 20 , 25 , 30 , 35 , 40 , 45 , 50 , 60}

36. Let us consider the below traversals:
•Inorder sequence: D B E A F C
•Preorder sequence: A B D E C F
Create binary tree.
In Preorder the leftmost node represents the root of the tree

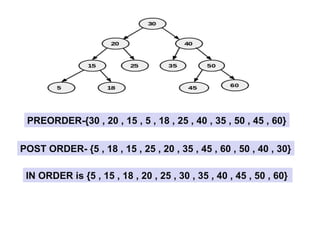
37. Input: in order = [9,3,15,20,7], post order =
[9,15,7,20,3]
Create Binary tree
In Post Order the right most node represents the root

38. Non Recursive Tree Traversal

39. Pre-order Traversal Without Recursion
The following operations are performed to traverse a binary
tree in pre-order using a stack:
1.Start with root node and push onto stack.
2.Repeat while the stack is not empty
2.1 POP the top element (PTR) from the stack and process
the node.
2.2 PUSH the right child of PTR onto to stack.
2.3 PUSH the left child of PTR onto to stack.

40. 1.
2.
4.
3.
Pre-order Traversal (Non Recursive Example)

41. 6.
5.
4.
7.

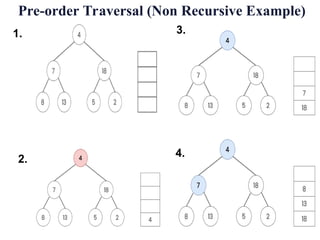
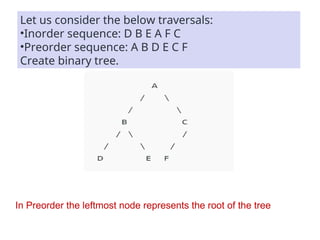
42. The nodes are processed in the order [ 4, 7, 8, 13,
18, 5, 2 ]
. This is the required preorder traversal of the given tree.
8.

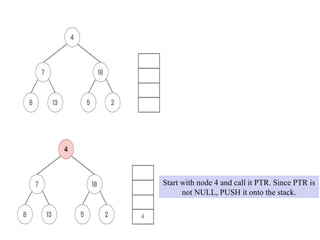
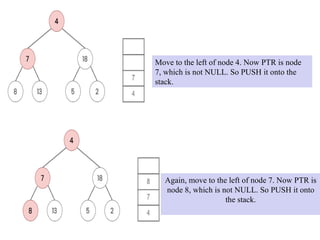
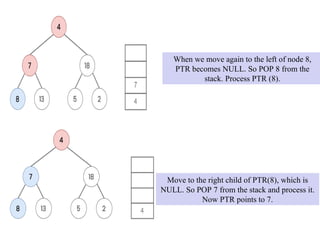
43. 1. Set TOP = 1. STACK[1] = NULL and PTR = ROOT.
2. Repeat Steps 3 to 5 while PTR ≠ NULL:
3. Apply PROCESS to PTR->DATA.
4. If PTR->RIGHT ≠ NULL, then:
Set TOP = TOP + 1, and STACK[TOP] = PTR->RIGHT.
[End of If]
5. If PTR->LEFT ≠ NULL, then:
Set PTR = PTR -> LEFT.
Else:
Set PTR = STACK[TOP] and TOP = TOP - 1.
[End of If]
[End of Step 2 loop.]
6. Exit.
Non Recursive Pre Order Traversal Algorithm

44. The following operations are performed to traverse a binary tree in in-
order using a stack:
1.Start from the root, call it PTR.
2.Push PTR onto stack if PTR is not NULL.
3.Move to left of PTR and repeat step 2.
4.If PTR is NULL and stack is not empty, then Pop element from stack
and set as PTR.
1.Process PTR and move to right of PTR , go to step 2.
In-order Traversal Without Recursion

45. Start with node 4 and call it PTR. Since PTR is
not NULL, PUSH it onto the stack.

46. Move to the left of node 4. Now PTR is node
7, which is not NULL. So PUSH it onto the
stack.
Again, move to the left of node 7. Now PTR is
node 8, which is not NULL. So PUSH it onto
the stack.

47. When we move again to the left of node 8,
PTR becomes NULL. So POP 8 from the
stack. Process PTR (8).
Move to the right child of PTR(8), which is
NULL. So POP 7 from the stack and process it.
Now PTR points to 7.

48. Move to the right child(13) of PTR and PUSH
it onto the stack.
Move to the left of node 13, which is NULL.
So POP 13 from the stack and process it.

49. Since node 13 don’t have any right child, POP
4 from the stack and process it. Now PTR
points to node 4.
Move to the right of node 4 and put it on to the
stack. Now PTR points to node 18.

50. Move to the left(5) child of 18 and put it onto
the stack. Now PTR points to node 5.
Move to the left of node 5, which is NULL. So
POP 5 from the stack and process it.

51. Move to the right(2) of node 18 and PUSH it
on to the stack.
Now, move to the right of node 5, which is
NULL. So POP 18 from the stack and process
it.

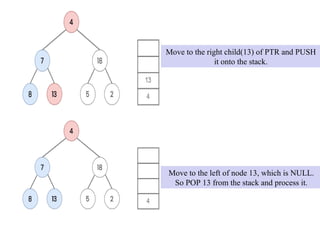
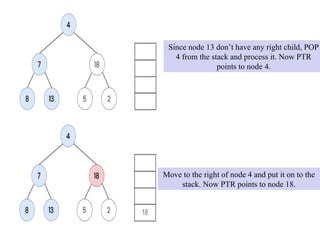
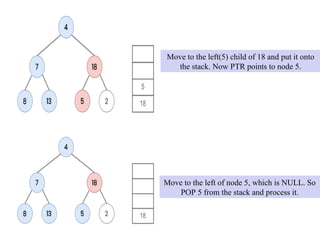
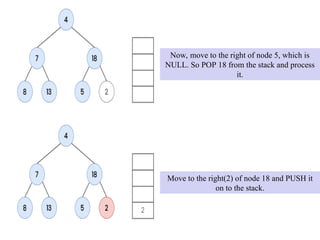
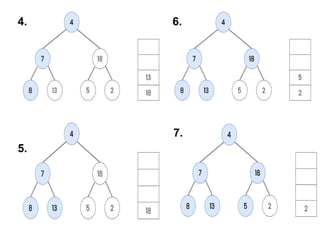
52. The nodes are processed in the order [ 8, 7, 13, 4, 5, 18, 2 ]
. This is the required in order traversal of the given tree.
Since node 2 has left child, POP 2 from the stack and process it. Now the
stack is empty and node 2 has no right child. So stop traversing

53. Binary Search Tree
A binary search tree (BST) or
"ordered binary tree" is a empty or in which
each node contains a key that satisfies
following conditions:
1. All keys are distinct.’
2. , all elements in its left subtree are less to the node
(<), and all the elements in its right subtree are greater
than the node (>).

54. Binary search tree
Binary search tree property
For every node X
All the keys in its left
subtree are smaller than
the key value in X
All the keys in its right
subtree are larger than the
key value in X

55. Binary Search Trees
A binary search tree Not a binary search tree
For more detail contact us