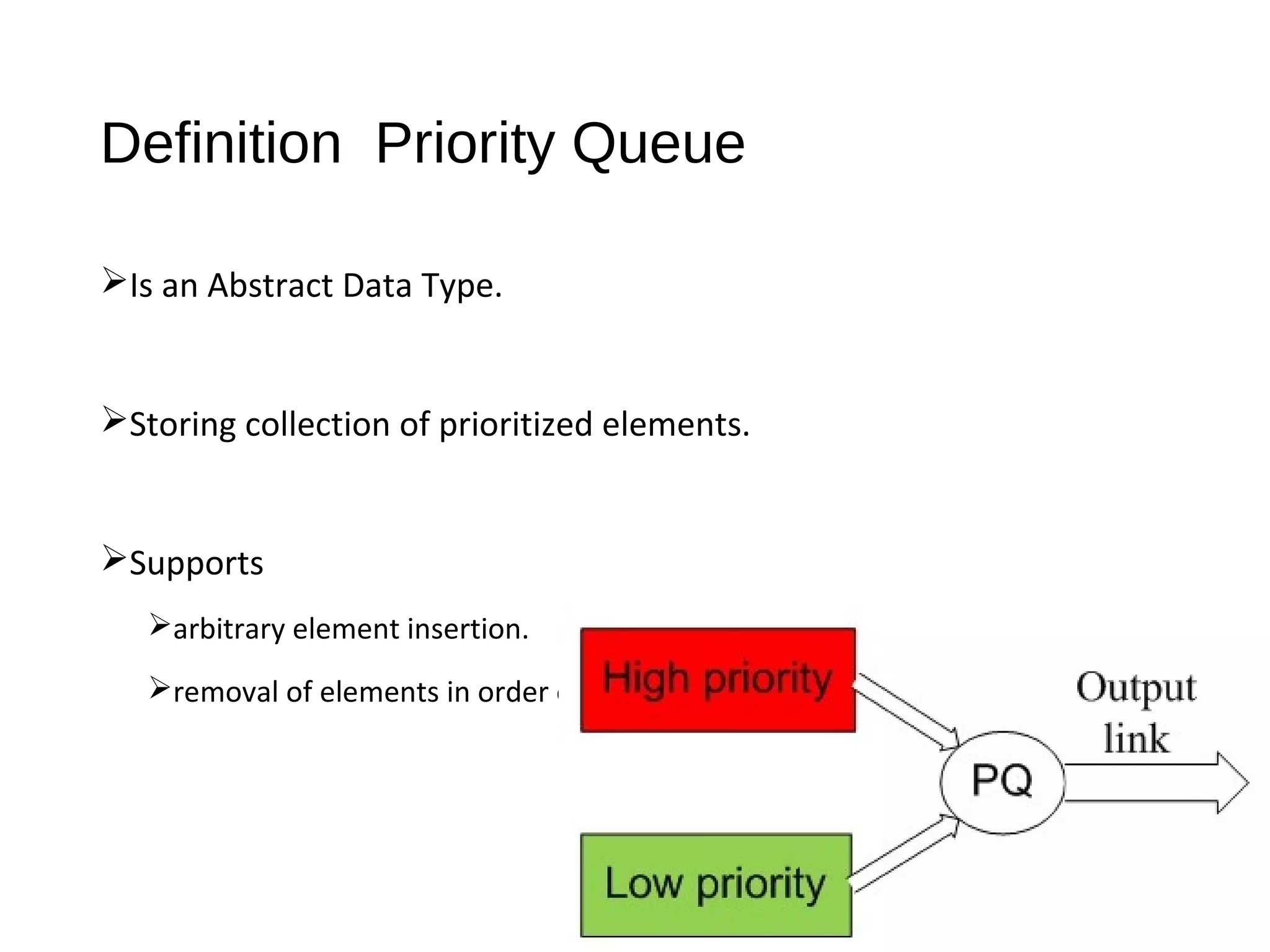
The document discusses priority queues as an abstract data type used for storing prioritized elements, where utility determines the importance of each asset. It outlines key operations and methods for managing priority queues, highlights their applications, and explains sorting methods involving priority queues. Additionally, it compares performance metrics for operations with unsorted and sorted lists.

1. Priority Queues
(Algorithms and Data Structures)
By
Priyanka Rana
By – Priyanka Rana

2. Priority Queues
Which assets (stock, company, real-estate) the company should
purchase for investment.

3. Priority Queues
Many factors determine the future value of an asset.
Let’s call this “Utility”.
Utility(asset) = priority or importance that Utility() return the
minimum value.
Use Utility() as key or order of assets in the list.

4. Definition Priority Queue
Is an Abstract Data Type.
Storing collection of prioritized elements.
Supports
arbitrary element insertion.
removal of elements in order of priority.

5. Priority Queue ADT
Each entry is a pair (key, value).
Key: used to identify or weigh that element.
Two distinct entries in a priority queue can have the same key.
Mathematical concept of total order relation, must satisfy:
Reflexive property: k ≤ k.
Antisymmetric property: if k1 ≤ k2 and k2 ≤ k1 , then k1 = k2.
Transitive property: if k1 ≤ k2 and k2 ≤ k3, then k1 ≤ k3.

6. Applications
Standby flyers.
Auctions.
Stock market.

7. Main methods of Priority Queue ADT
size():
Return the number of entries in the queue.
isEmpty():
Test whether the queue is empty.
min():
Return (do not remove) an entry with smallest key.
insert(k, x):
Insert an entry with key k and value x.
removeMin():
Remove and return the entry with smallest key.

8. Sorting with a Priority Queue
Sorting a collection S of n comparable elements
with a priority queue Q, called PriorityQueueSort.
Hint: Using insert() and removeMin()

9. Exercise
Operation Output
Insert(5,A) nil
Insert(4,B) nil
Insert(7,I) nil
removeMin() (4,B)
insert(3,J) Nil
removeMin() (3,J)
insert(6,L) nil
removeMin() (5,A)

10. Implementing a Priority Queue
• With an unsorted list :
• insert() – adds entry at last -> takes O(1)
• removeMin() – requires complete scan -> takes O(n)
• “fast insertion and slow removal”
4 5 2 3 1

11.  With a Sorted List:
 Insert() – requires complete scan -> takes O(n)
 removeMin() – always access the first element -> takes O(1)
 fast removal and slow insertions.
1 2 3 4 5

12. Method Unsorted List Sorted List
size, isEmpty O(1) O(1)
insert O(1) O(n)
Min, removeMin O(n) O(1)

13. Sorting using priority Queues
• Selection – Sort
• Insertion - Sort

14. Selection Sort – 7 4 8 2 5 3 9
7 4 8 2 5 3 9
2 4 8 7 5 3 9
2 3 8 7 5 4 9
2 3 4 7 5 8 9
2 3 4 5 7 8 9
2 3 4 5 7 8 9
2 3 4 5 7 8 9

15. Selection- Sorting using priority Queues
Sequence S Priority Queue P
Input (7,4,8,2,5,3,9) ()
Phase 1 (a)
(b)
.
.
.
(g)
(4,8,2,5,3,9)
(8,2,5,3,9)
.
.
.
()
(7)
(7,4)
.
.
.
(7,4,8,2,5,3,9)
Phase 2 (a)
(b)
(c)
(d)
(e)
(f)
(g)
(2)
(2,3)
(2,3,4)
(2,3,4,5)
(2,3,4,5,7)
(2,3,4,5,7,8)
(2,3,4,5,7,8,9)
(7,4,8,2,5,3,9)
(7,4,8,5,9)
(7,8,5,9)
(7,8,9)
(8,9)
(9)
()

16. Running Time
• First removeMin takes O(n) time
• Second removeMin takes O(n-1) time) and so on
• Till last n operation takes O(1) time
= O(n2)O(n

17. Insertion Sort – 7 4 8 2 5 3 9
7
4 7
4 7 8
2 4 7 8
2 3 4 5 7 8 9
2 3 4 5 7 8
2 4 5 7 8

18. Insertion -Sorting using priority Queues
Sequence S Priority Queue P
Input (7,4,8,2,5,3,9) ()
Phase 1 (a)
(b)
(c)
(d)
(e)
(f)
(g)
(4,8,2,5,3,9)
(8,2,5,3,9)
(2,5,3,9)
(5,3,9)
(3,9)
(9)
()
(7)
(4,7)
(4,7,8)
(2,4,7,8)
(2,4,5,7,8)
(2,3,4,5,7,8)
(2,3,4,5,7,8,9)
Phase 2 (a)
(b)
●
.
(2)
(2,3)
● .
● .
● .
(2,3,4,5,7,8,9)
(3,4,5,7,8,9)
(4,5,7,8,9)
.
.
.
()

19. Running Time
• First element -no comparison
• Second element – 1 comparison
• Third element – 2 comparisons and so on.
= O(n2)O(n

20. THANK YOU