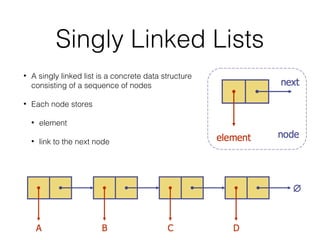
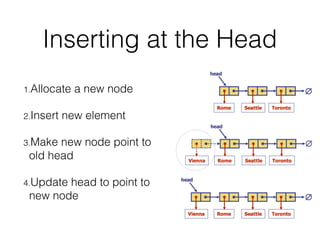
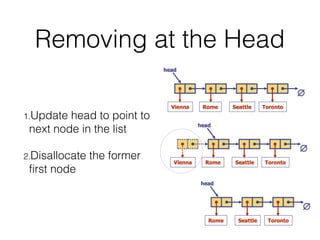
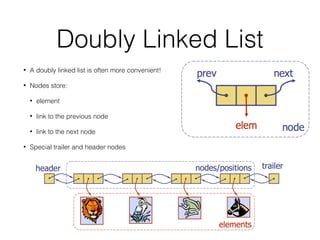
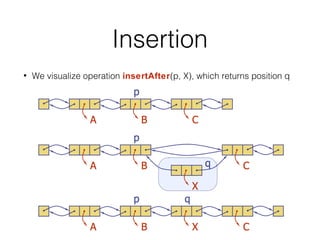
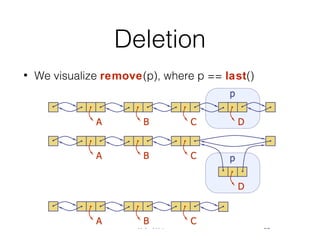
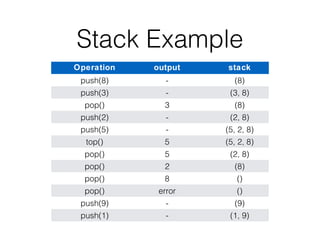
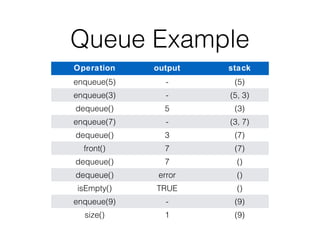
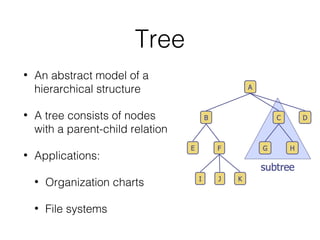
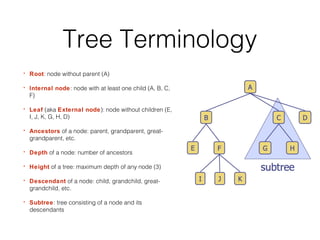
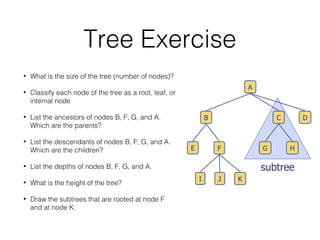
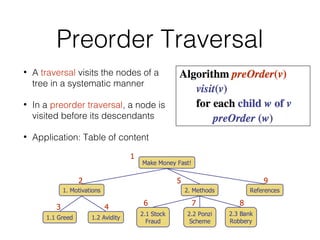
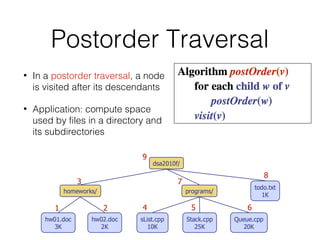
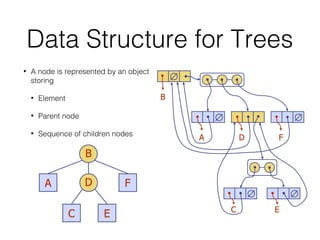
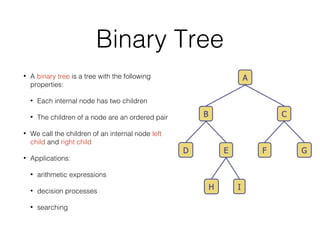
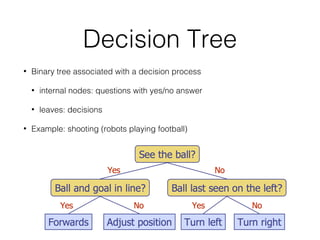
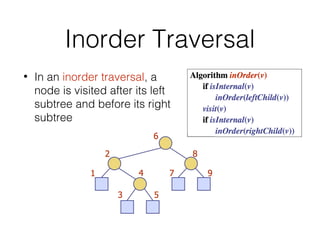
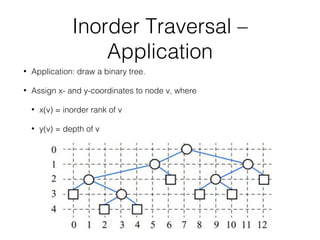
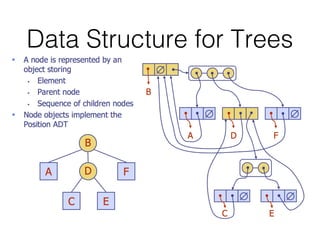
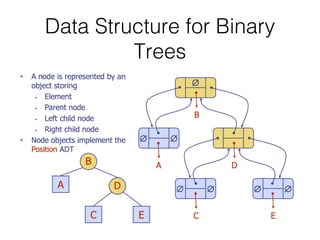
This document covers different data structures including arrays, lists, stacks, queues, and trees. It describes the basic operations and applications of each structure. For trees specifically, it defines common tree terminology, covers tree traversal methods like preorder and postorder, and describes binary trees and their properties. It provides examples of using trees to represent arithmetic expressions and decision processes.

1. Lesson 4
Data Structure

2. Arrays
• Built-in in most programming languages
• Two kinds (programmer responsibility):
• Unordered: attendance tracking
• Ordered: high scorers
• Operations:
• Insertion
• Deletion
• Search

3. List
• The List models a sequence of positions
storing arbitrary objects
• It establishes a before/after relation
between positions
• Generic methods:
• size(), isEmpty()
• Accessor methods:
• first(), last()
• prev(p), next(p)
• Update methods:
• replace(p, e)
• insertBefore(p, e),
• insertAfter(p, e),
• insertFirst(e),
• insertLast(e)
• remove(p)

4. Singly Linked Lists
• A singly linked list is a concrete data structure
consisting of a sequence of nodes
• Each node stores
• element
• link to the next node

5. Inserting at the Head
1.Allocate a new node
2.Insert new element
3.Make new node point to
old head
4.Update head to point to
new node

6. Removing at the Head
1.Update head to point to
next node in the list
2.Disallocate the former
first node

7. Doubly Linked List
• A doubly linked list is often more convenient!
• Nodes store:
• element
• link to the previous node
• link to the next node
• Special trailer and header nodes

8. Insertion
• We visualize operation insertAfter(p, X), which returns position q

9. Deletion
• We visualize remove(p), where p == last()

10. Stack
• The stack is a very common data structure used in
programs which has lot of potential
• Hold object, usually all of the same type
• Follows the concept of LIFO

11. Stack
• Main stack operations:
• push(object): inserts an element
• pop(): removes and returns the last inserted
element
• Auxiliary stack operations:
• top(): returns the last inserted element without
removing it
• size(): returns the number of elements stored
• isEmpty(): returns a Boolean value indicating
whether no elements are stored

12. Stack Example
Operation output stack
push(8) - (8)
push(3) - (3, 8)
pop() 3 (8)
push(2) - (2, 8)
push(5) - (5, 2, 8)
top() 5 (5, 2, 8)
pop() 5 (2, 8)
pop() 2 (8)
pop() 8 ()
pop() error ()
push(9) - (9)
push(1) - (1, 9)

13. Application of Stack
• Direct applications
★ Page-visited history in a Web browser
★ Undo sequence in a text editor
• Indirect applications
★ Auxiliary data structure for algorithms
★ Component of other data structures

14. Queue
• The stack is a very common data structure used in
programs which has lot of potential
• Hold object, usually all of the same type
• Follows the concept of FIFO
• Insertions are at the rear of the queue and removals
are at the front of the queue

15. Queue
• Main queue operations:
• enqueue(o): inserts element o at the end of the queue
• dequeue(): removes and returns the element at the
front of the queue
• Auxiliary queue operations:
• front(): returns the element at the front without removing
it
• size(): returns the number of elements stored
• isEmpty(): returns a Boolean value indicating whether
no elements are stored

16. Queue Example
Operation output stack
enqueue(5) - (5)
enqueue(3) - (5, 3)
dequeue() 5 (3)
enqueue(7) - (3, 7)
dequeue() 3 (7)
front() 7 (7)
dequeue() 7 ()
dequeue() error ()
isEmpty() TRUE ()
enqueue(9) - (9)
size() 1 (9)

17. Application of Queue
• Direct applications
★ Waiting lists
★ Access to shared resources (e.g., printer)
• Indirect applications
★ Auxiliary data structure for algorithms
★ Component of other data structures

18. Tree
• An abstract model of a
hierarchical structure
• A tree consists of nodes
with a parent-child relation
• Applications:
• Organization charts
• File systems

19. Tree Terminology
• Root: node without parent (A)
• Internal node: node with at least one child (A, B, C,
F)
• Leaf (aka External node): node without children (E,
I, J, K, G, H, D)
• Ancestors of a node: parent, grandparent, great-
grandparent, etc.
• Depth of a node: number of ancestors
• Height of a tree: maximum depth of any node (3)
• Descendant of a node: child, grandchild, great-
grandchild, etc.
• Subtree: tree consisting of a node and its
descendants

20. Tree Exercise
• What is the size of the tree (number of nodes)?
• Classify each node of the tree as a root, leaf, or
internal node
• List the ancestors of nodes B, F, G, and A.
Which are the parents?
• List the descendants of nodes B, F, G, and A.
Which are the children?
• List the depths of nodes B, F, G, and A.
• What is the height of the tree?
• Draw the subtrees that are rooted at node F
and at node K.

21. Tree
• Generic methods:
• integer size()
• boolean isEmpty()
• objectIterator elements()
• positionIterator positions()
• Accessor methods:
• position root()
• position parent(p)
• positionIterator children(p)
• Query methods:
• boolean isInternal(p)
• boolean isLeaf (p)
• boolean isRoot(p)
• Update methods:
• swapElements(p, q)
• object replaceElement(p, o)

22. Depth and Height
• v : a node of a tree T.
• The depth of v is the number
of ancestors of v, excluding v
itself.
• The height of a node v in a
tree T is defined recursively:
• If v is an external node, then
the height of v is 0
• Otherwise, the height of v is
one plus the maximum
height of a child of v.

23. Preorder Traversal
• A traversal visits the nodes of a
tree in a systematic manner
• In a preorder traversal, a node is
visited before its descendants
• Application: Table of content

24. Postorder Traversal
• In a postorder traversal, a node
is visited after its descendants
• Application: compute space
used by files in a directory and
its subdirectories

25. Data Structure for Trees
• A node is represented by an object
storing
• Element
• Parent node
• Sequence of children nodes

26. Binary Tree
• A binary tree is a tree with the following
properties:
• Each internal node has two children
• The children of a node are an ordered pair
• We call the children of an internal node left
child and right child
• Applications:
• arithmetic expressions
• decision processes
• searching

27. Binary Tree
• The BinaryTree extends the Tree, i.e., it inherits all the
methods of the Tree
• Update methods may be defined by data structures
implementing the BinaryTree
• Additional methods:
• position leftChild(p)
• position rightChild(p)
• position sibling(p)

28. Arithmetic Expression Tree
• Binary tree associated with an arithmetic expression
• internal nodes: operators
• leaves: operands
• Example: arithmetic expression tree for the expression (2 × (a − 1) + (3 × b))

29. Decision Tree
• Binary tree associated with a decision process
• internal nodes: questions with yes/no answer
• leaves: decisions
• Example: shooting (robots playing football)

30. Properties of Binary Trees

31. Inorder Traversal
• In an inorder traversal, a
node is visited after its left
subtree and before its right
subtree

32. Inorder Traversal –
Application
• Application: draw a binary tree.
• Assign x- and y-coordinates to node v, where
• x(v) = inorder rank of v
• y(v) = depth of v

33. Exercise
• Draw a (single) binary tree T, such that
• Each internal node of T stores a single character
• A preorder traversal of T yields EXAMFUN
• An inorder traversal of T yields MAFXUEN

34. Print Arithmetic Expressions

35. Evaluate Arithmetic
Expressions

36. Exercise
1.Draw an expression tree that has
• Four leaves, storing the values 1, 5, 6, and 7
• 3 internal nodes, storing operations +, -, *, /(operators can be used more
than once, but each internal node stores only one)
• The value of the root is 21
2. Draw a tree that represents the expression (3*45 + 10*(6-2))-(5/6 + 7*2)
• list all the internal nodes, leaf nodes. What are the height and the size of
the tree?
• list all nodes in the order visited using preorder/postorder/inorder
traversal.

37. Data Structure for Trees

38. Data Structure for Binary
Trees