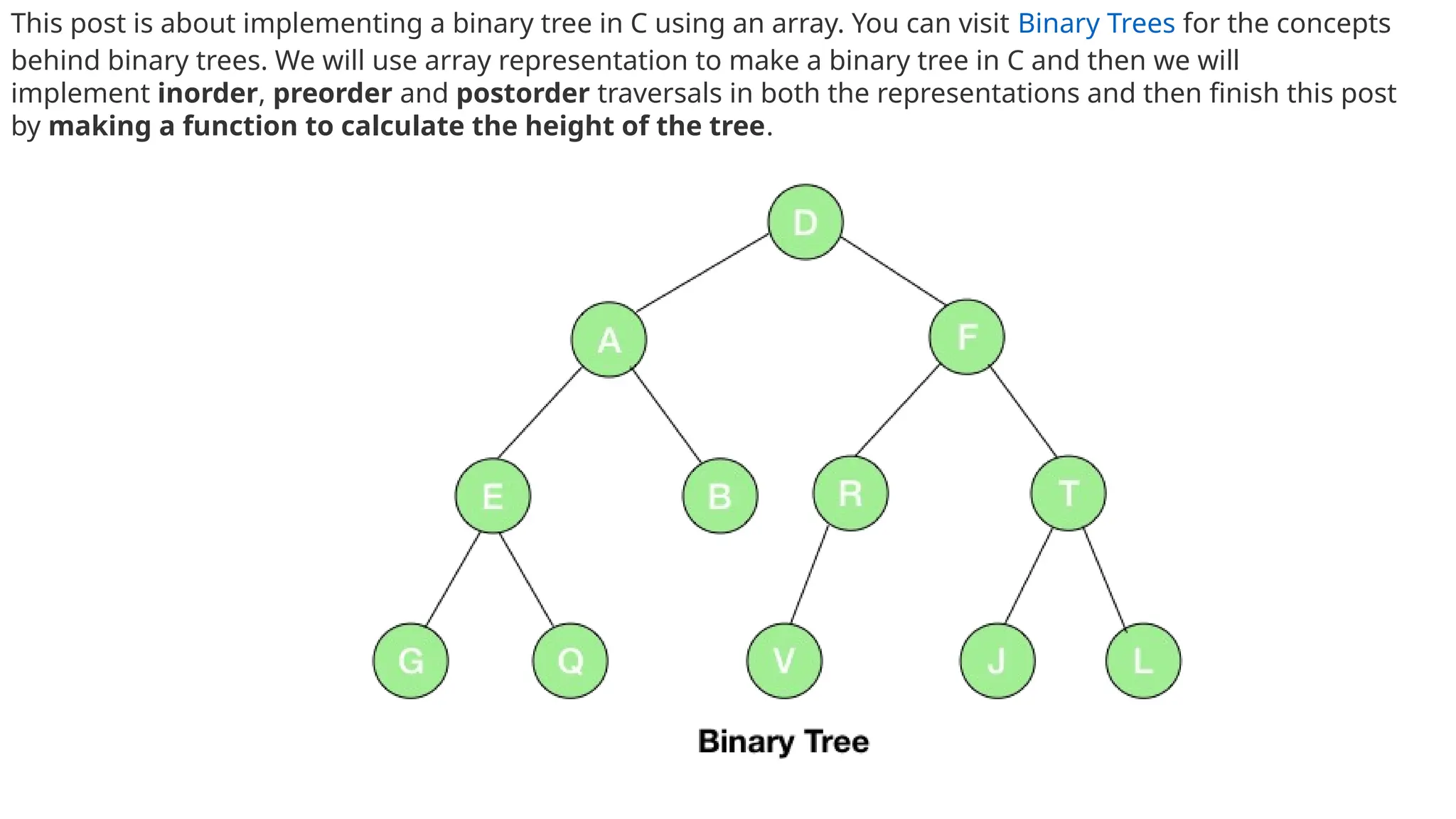
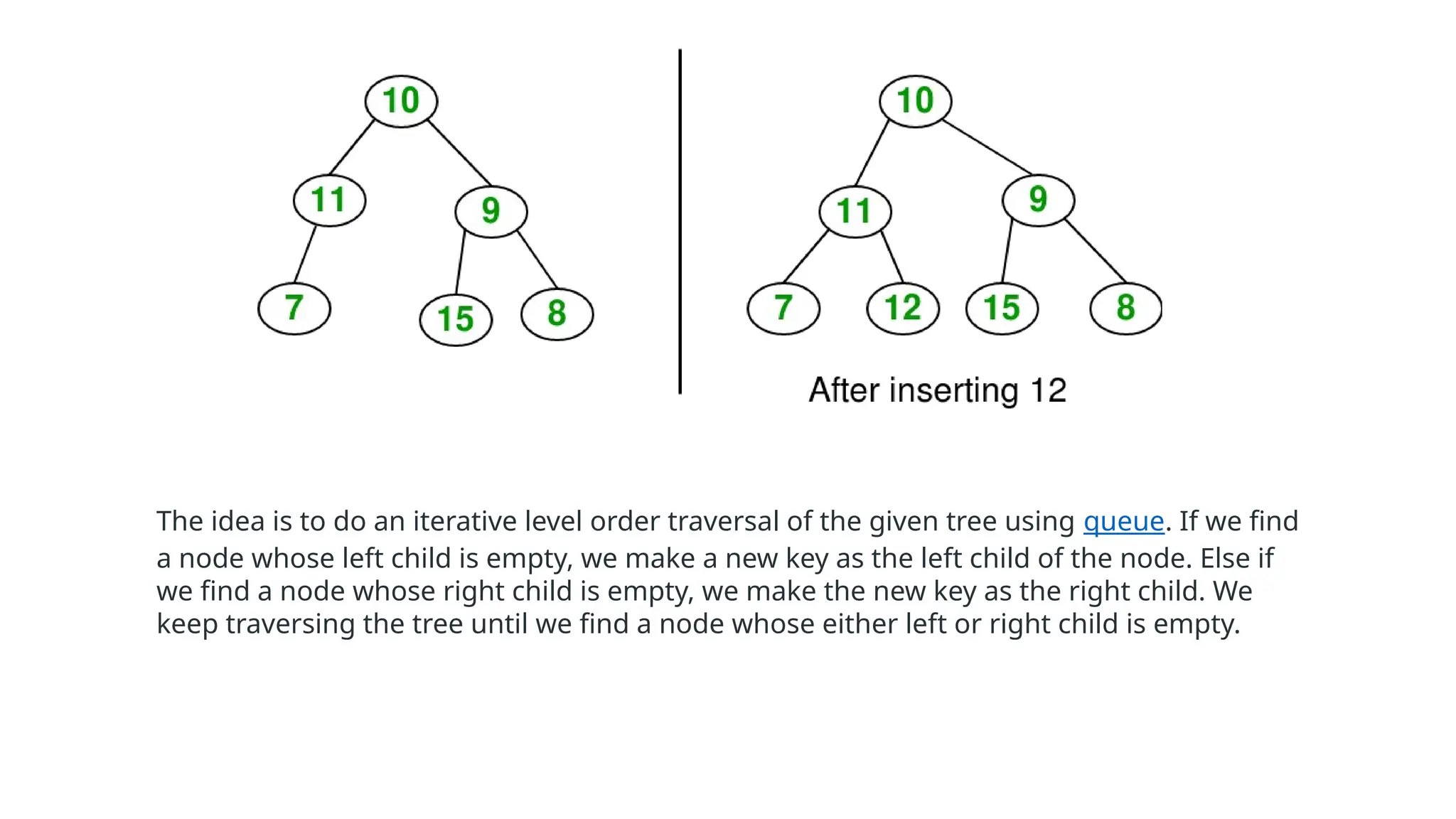
The document discusses the implementation of binary trees using arrays, explaining how an array can represent tree nodes with parent-child relationships. It covers operations such as insertion, deletion, and traversal methods including inorder, preorder, and postorder. Additionally, it addresses applications of binary trees in areas like data storage, expression evaluation, and memory allocation.

1. Implementation of Tree
Using Arrays
(Binary Tree)

2. Binary Tree (Array
implementation)
Given an array that represents a tree in such a way that array indexes are values in tree nodes and array
values give the parent node of that particular index (or node). The value of the root node index would always
be -1 as there is no parent for root. Construct the standard linked representation of given Binary Tree from
this given representation.
Do refer in order to understand how to construct binary tree from given parent array representation.
Ways to represent:
Trees can be represented in two ways as listed below:
1.Dynamic Node Representation (Linked Representation).
2.Array Representation (Sequential Representation).
Now, we are going to talk about the sequential representation of the trees. In order to represent a tree using
an array, the numbering of nodes can start either from 0–(n-1) or 1– n, consider the below illustration as
follows:
Binary Tree Representation
A Binary tree is represented by a pointer to the topmost node (commonly known as the “root”) of the tree. If
the tree is empty, then the value of the root is NULL. Each node of a Binary Tree contains the following parts:
1.Data
2.Pointer to left child
3.Pointer to right child
Basic Operation On Binary Tree:
•Inserting an element.
•Removing an element.
•Searching for an element.

3. Auxiliary Operation On Binary Tree:
•Finding the height of the tree
•Find the level of a node of the tree
•Finding the size of the entire tree.
Topic :
•Introduction
•Basic Operation
•Traversals
•Standard Problems on Binary Trees
Introduction :
1.Introduction to Binary Tree – Data Structure and Algorithm Tutorials
2.Properties of Binary Tree
3.Types of Binary Tree
4.Applications, Advantages and Disadvantages of Binary Tree
5.Binary Tree (Array implementation)
6.Complete Binary Tree
7.Perfect Binary Tree

4. Basic Operations on Binary Tree:
1.Tree Traversals (Inorder, Preorder and Postorder)
2.Level Order Tree Traversal
3.Find the Maximum Depth or Height of given Binary Tree
4.Insertion in a Binary Tree
5.Deletion in a Binary Tree
6.Enumeration of Binary Trees
Some other important Binary Tree Traversals :
1.Level order traversal in spiral form
2.Reverse Level Order Traversal
3.BFS vs DFS for Binary Tree
4.Inorder Tree Traversal without Recursion
5.Morris traversal for Preorder
6.Iterative Preorder Traversal
7.Iterative Postorder Traversal Using Two Stacks
8.Diagonal Traversal of Binary Tree
9.Boundary Traversal of binary tree
More >>

5. n C : Array Representation and Traversals
This post is about implementing a binary tree in C using an array. You can visit Binary Trees for the concepts
behind binary trees. We will use array representation to make a binary tree in C and then we will
implement inorder, preorder and postorder traversals in both the representations and then finish this post
by making a function to calculate the height of the tree.

6. We will use the above tree for the array representation. As discussed in the post Binary Trees, the array we will use
to represent the above tree will be:
Let’s start with the first step and make an array.
A binary tree is a tree data structure in which each node can have at most two children, which are referred to as
the left child and the right child.
The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. A binary
tree can be visualized as a hierarchical structure with the root at the top and the leaves at the bottom.
Binary trees have many applications in computer science, including data storage and retrieval, expression
evaluation, network routing, and game AI. They can also be used to implement various algorithms such as
searching, sorting, and graph algorithms.
Basic Operations On Binary Tree:
•Inserting an element.
•Removing an element.
•Searching for an element.
•Deletion for an element.
•Traversing an element. There are four (mainly three) types of traversals in a
binary tree which will be discussed ahead.

7. Applications of Binary Tree:
•In compilers, Expression Trees are used which is an application of binary trees.
•Huffman coding trees are used in data compression algorithms.
•Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1)
time complexity.
•Represent hierarchical data.
•Used in editing software like Microsoft Excel and spreadsheets.
•Useful for indexing segmented at the database is useful in storing cache in the system,
•Syntax trees are used for most famous compilers for programming like GCC, and AOCL to perform arithmetic
operations.
•For implementing priority queues.
•Used to find elements in less time (binary search tree)
•Used to enable fast memory allocation in computers.
•Used to perform encoding and decoding operations.
•Binary trees can be used to organize and retrieve information from large datasets, such as in inverted index
and k-d trees.
•Binary trees can be used to represent the decision-making process of computer-controlled characters in
games, such as in decision trees.
• Binary trees can be used to implement searching algorithms, such as in binary search trees which can be used
to quickly find an element in a sorted list.
•Binary trees can be used to implement sorting algorithms, such as in heap sort which uses a binary heap to
sort elements efficiently.

8. Basic Operations On Binary Tree:
•Inserting an element.
•Removing an element.
•Searching for an element.
•Deletion for an element.
•Traversing an element. There are four (mainly three) types of traversals in a binary
tree which will be discussed ahead.
Auxiliary Operations On Binary Tree:
•Finding the height of the tree
•Find the level of the tree
•Finding the size of the entire tree.
Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:
•Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or
right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first
then its left child and finally the right child.
•Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree
but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It
means that the left child is traversed first then its root node and finally the right child.
•Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and
right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first
then the right child and finally its root node.

9. The idea is to do an iterative level order traversal of the given tree using queue. If we find
a node whose left child is empty, we make a new key as the left child of the node. Else if
we find a node whose right child is empty, we make the new key as the right child. We
keep traversing the tree until we find a node whose either left or right child is empty.

10. Tree Terminologies
Various terminologies are related to the tree :
Root :
The first node of the binary tree is known as the root node of the binary tree. There
cannot be any tree without a root node, as it is the tree's origin, and the root node
has no parent element. We cannot have more than one root node in a tree.
Edge :
The connecting link between the two nodes is known as the edges of the tree. It is
also referred to as the branch of a tree. If there are n nodes in a binary tree, there
will be a total of n-1 edges.
Parent :
A node that has a connecting link to another node in the level below is known as a
parent node. In a more formal term, a node that is a predecessor of another node
is called a parent node.
Ancestors :.
Ancestors of a node are the nodes in the path from the root to the current
node, including the root node, and excluding the current node are ancestors of
the current node

11. Child :
Any node connected to a node one level above it is known as the child node. In
formal terms, every note that is a descendant of any node is known as a child node.
Every not present in the tree can be considered as a child node except the root
node.
Siblings :
The children node that shares the same parent node are referred to as siblings.
Leaf :
A node with no child is known as a leaf node. It is the terminal node of the tree.
Internal Node :
The nodes with at least one child node are known as internal nodes. Every node
(even the root node) is internal except the leaf nodes.
External Node :
A node with no child node is considered an external
node.
Height :
The height of any node is given by the of maximum number edges
from the leaf node to that particular node.

12. Binary search is a highly efficient search algorithm to locate a specific target value within a sorted array or
list. It operates by repeatedly dividing the search interval in half, significantly reducing the number of
comparisons required to find the target. The algorithm begins by examining the middle element of the array
and comparing it to the target. If the middle element matches the target, the search concludes successfully.
If the middle element is greater than the target, the search continues in the left half of the array; if it’s
smaller, the search continues in the right half. This process iterates until the target is found or the search
interval becomes empty.
Due to its halving nature, Binary search complexity exhibits an impressive time complexity of O(log n), where
n represents the number of elements in the array. This makes binary search particularly effective for large
datasets, offering a substantial improvement over linear search algorithms with a time complexity of O(n).
However, binary search demands a precondition of sorted data, which might necessitate sorting the array
initially. While incredibly efficient for sorted data, binary search is less suitable for small or frequently
changing data due to the initial sorting overhead.
Conclusion: