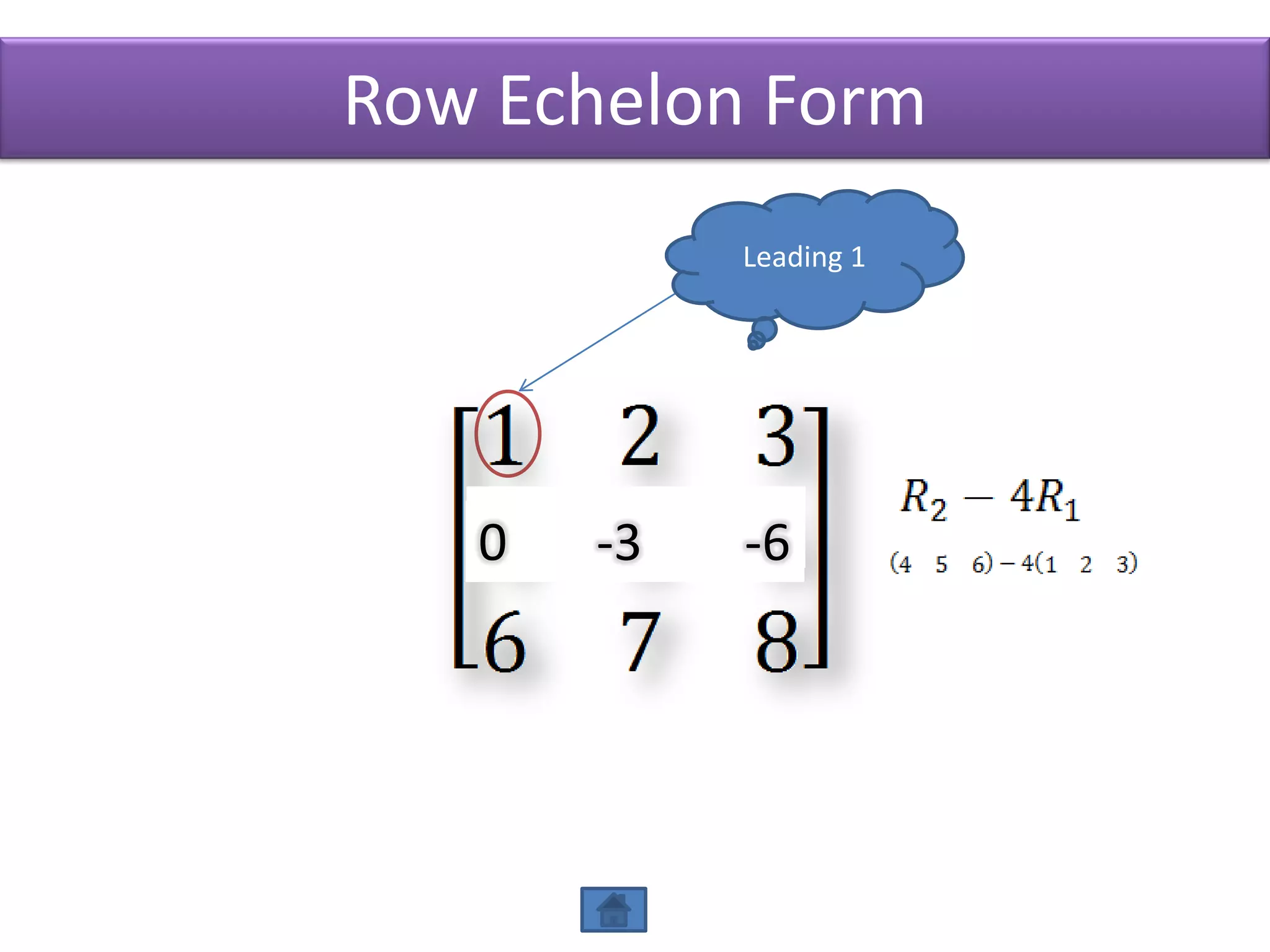
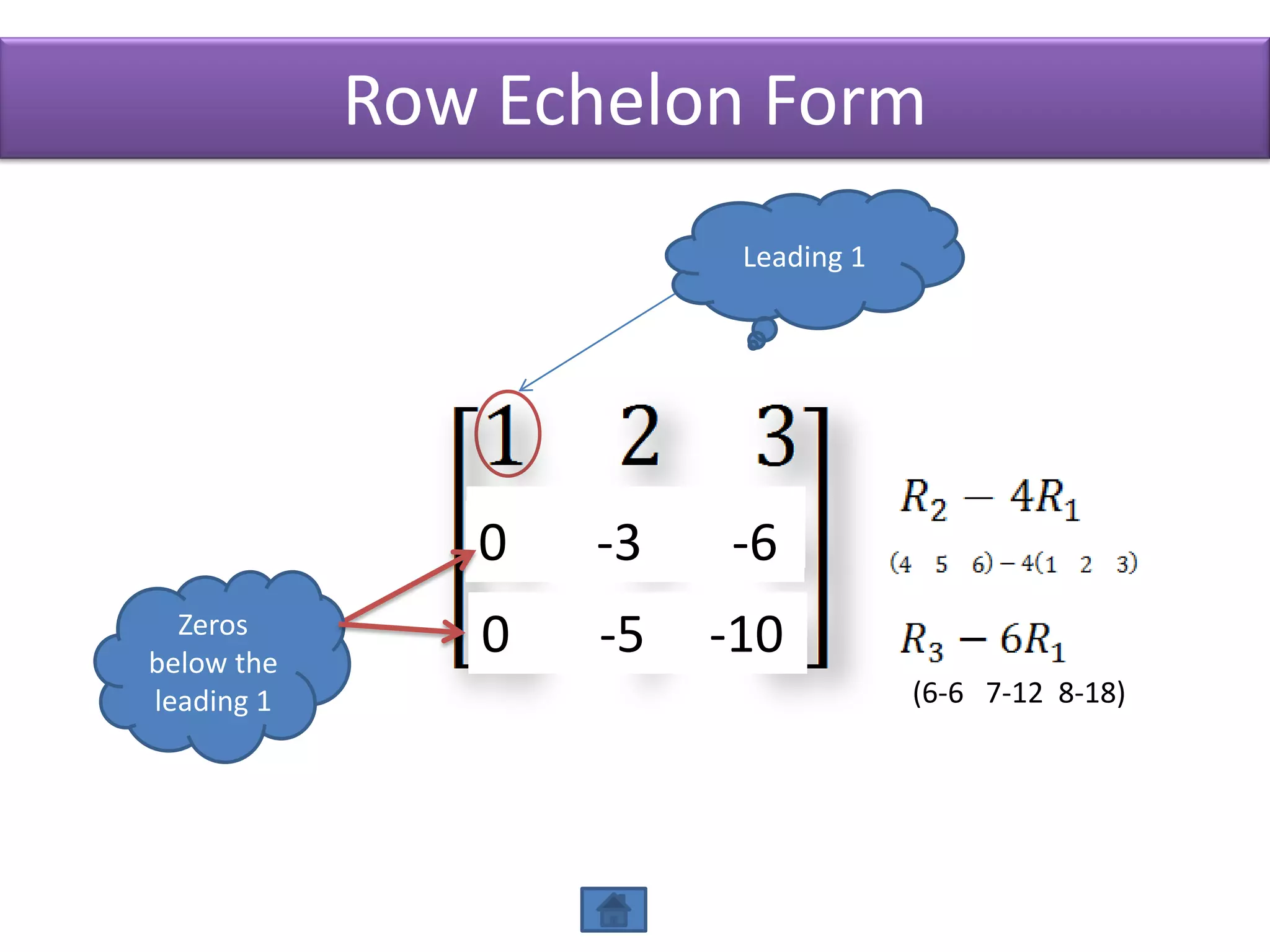
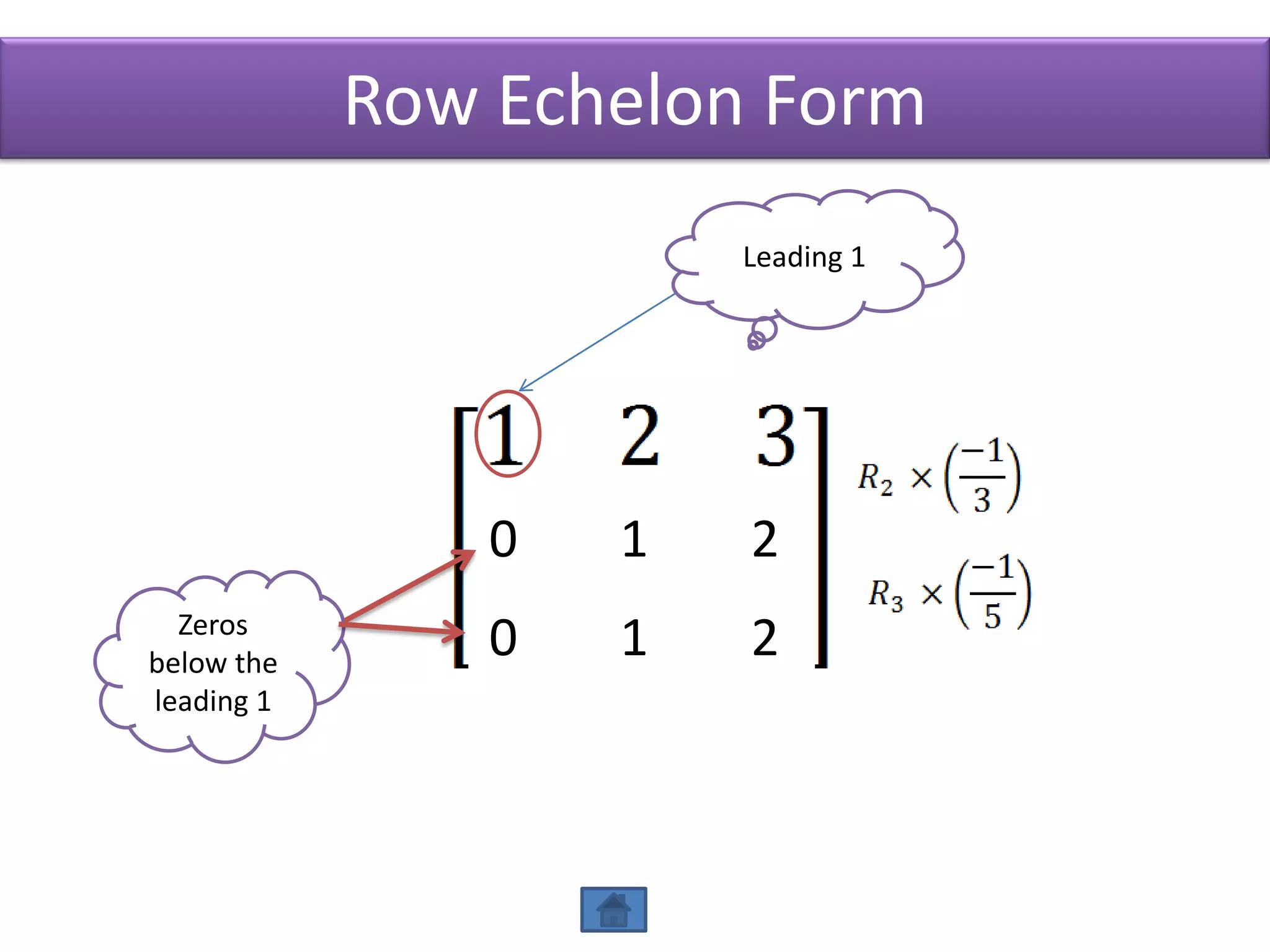
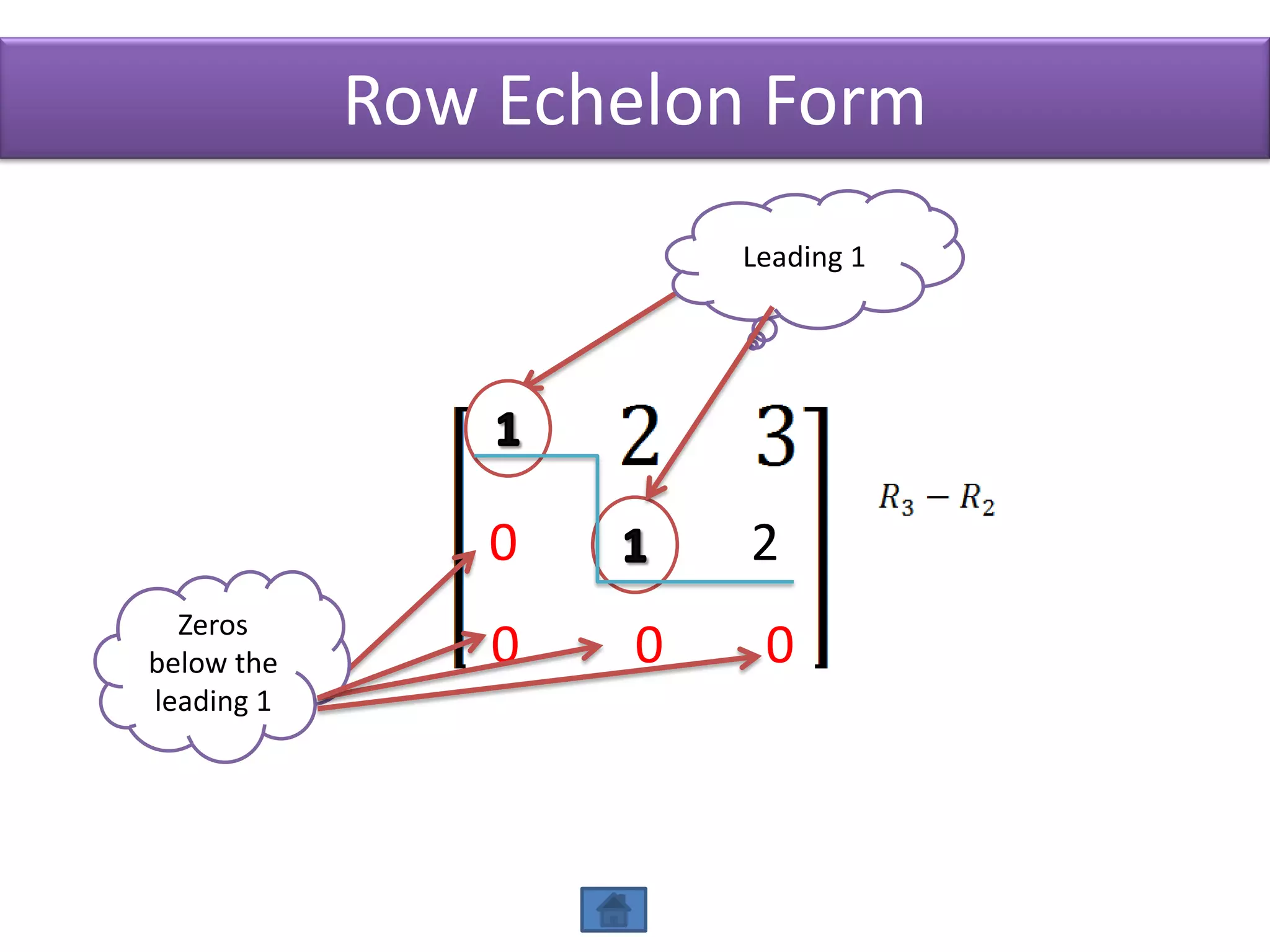
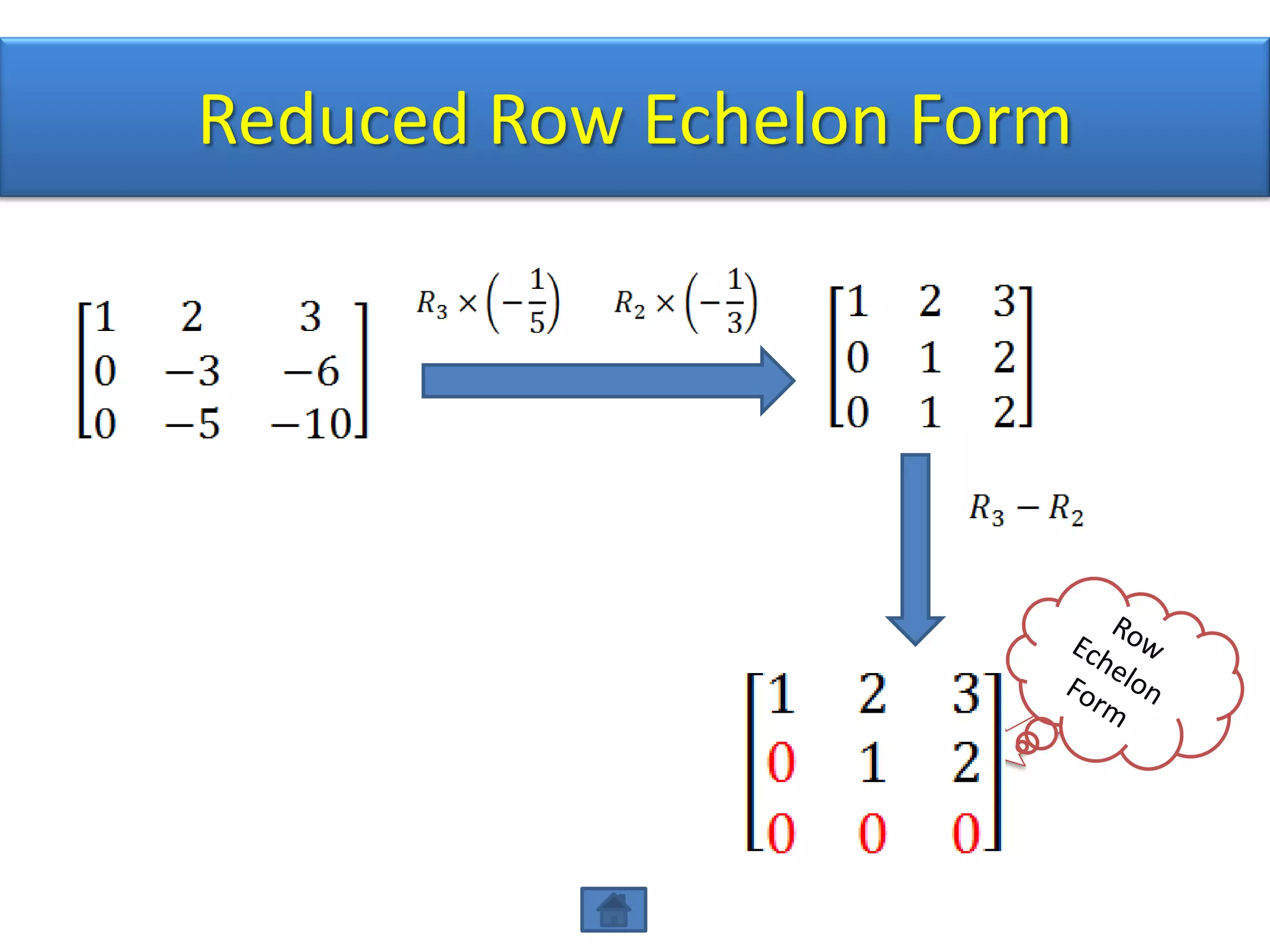
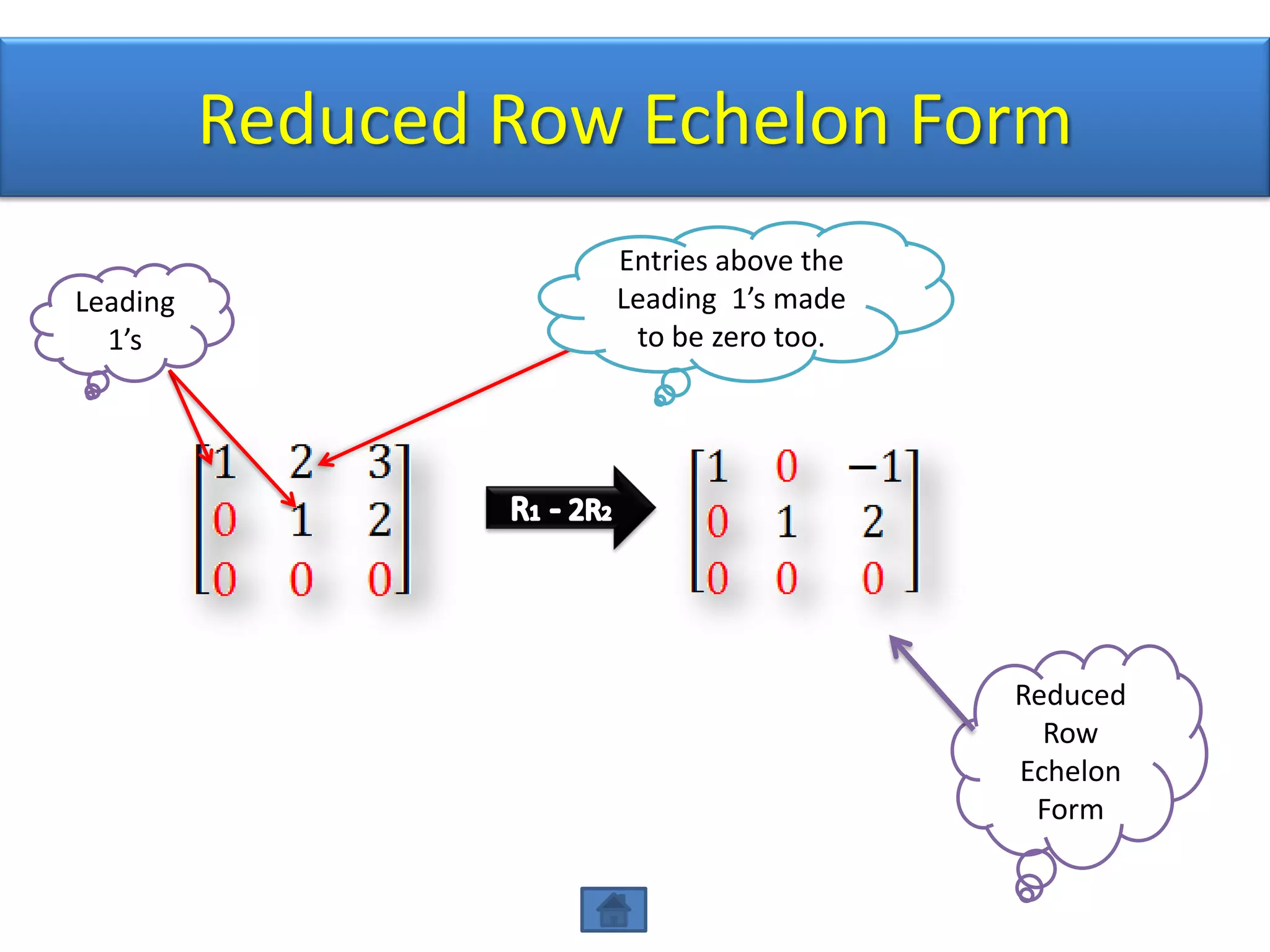
The document defines row echelon form and reduced row echelon form for matrices. Row echelon form requires that leading 1's occur farther to the right in lower rows. Reduced row echelon form further requires that all entries above leading 1's are zero. The document also discusses Gauss elimination method and elementary row operations for transforming a matrix into row echelon or reduced row echelon form.

1. Prepared By :-
Prof. K.K.Pokar
Government Engineering College Bhuj

6. Definition of Row Echelon &
Reduced Row Echelon Forms
Row Echelon Form
Reduced Row Echelon Form

7. If a row doesn’t
consist entirely of
zeros, then the
first non zero
number in the row
is a 1. We call this
as leading 1.
If there are any
rows that consist
entirely of zeros ,
then they are
grouped together
at Bottom of the
matrix.
In any two
successive rows that
do not consist
entirely of zeros, the
leading 1 in the
lower row occurs
farther to the right
than the leading 1 in
the higher row.
Each column that
contains a leading
1 has zeros
everywhere else
in that column.
Reduced Row Echelon Form
Gauss Jordan Gauss Jordan

8. 4-4 5-8 12-30 -3 -6
Leading 1
Gauss Elimination MethodRow Echelon Form

9. Gauss Elimination Method
4-4 5-8 12-30 -3 -6
Leading 1
Zeros
below the
leading 1 (6-6 7-12 8-18)
0 -5 -10
Row Echelon Form

10. Gauss Elimination Method
4-4 5-8 12-30 -3 -6
Leading 1
Zeros
below the
leading 1
0 -5 -10
0 1 2
0 1 2
Row Echelon Form

11. Gauss Elimination Method
4-4 5-8 12-30 -3 9
Leading 1
Zeros
below the
leading 1
0 -5 -10
0 1 2
0 1 20 0 0
Row Echelon Form

12. Row Echelon Form
Elementary Raw Operations

13. Row Echelon Form
Reduced Row Echelon Form

14. Reduced Row Echelon Form

15. Reduced Row Echelon Form

16. Reduced Row Echelon Form

17. Reduced Row Echelon Form
Entries above the
Leading 1’s made
to be zero too.
Leading
1’s
Reduced
Row
Echelon
Form