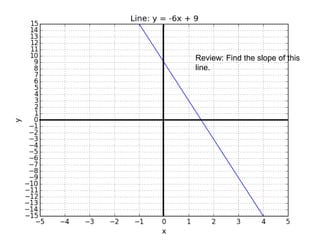
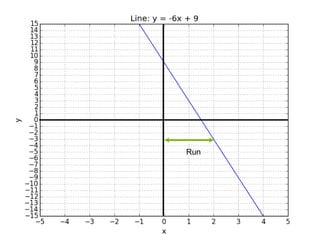
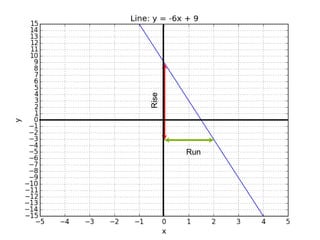
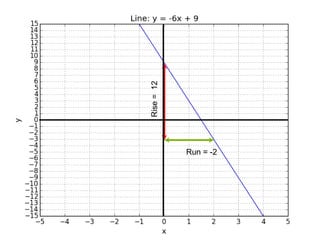
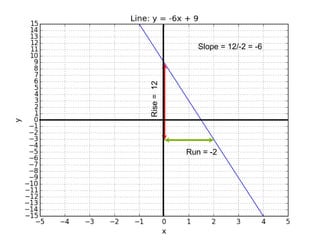
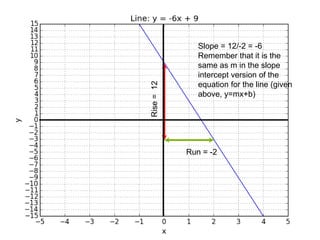
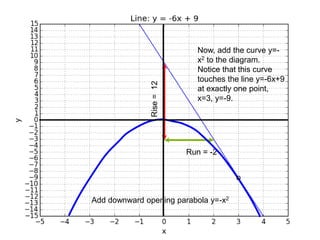
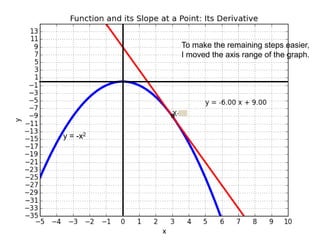
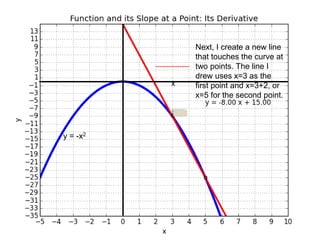
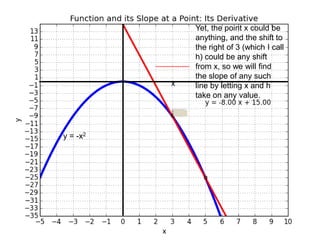
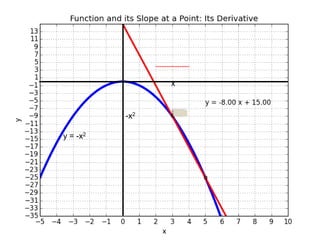
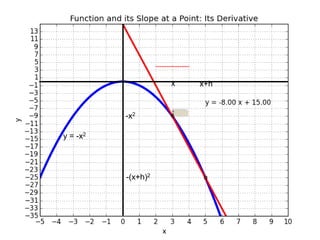
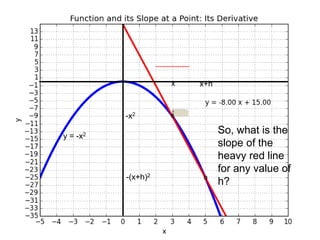
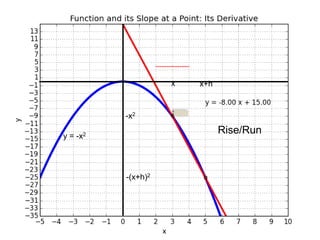
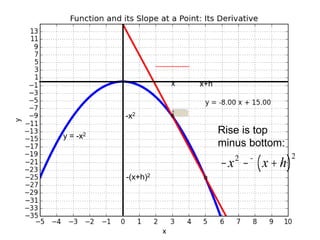
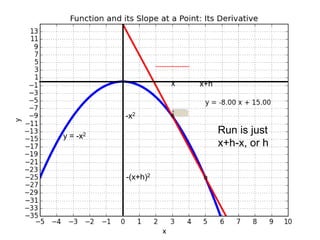
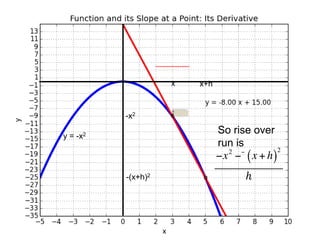
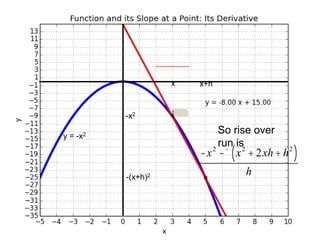
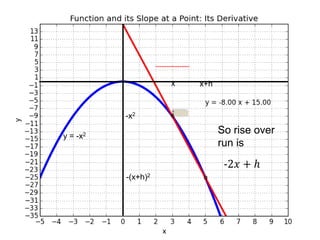
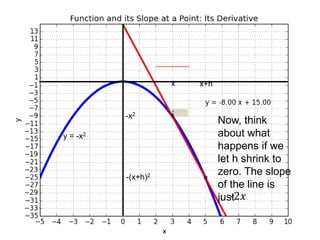
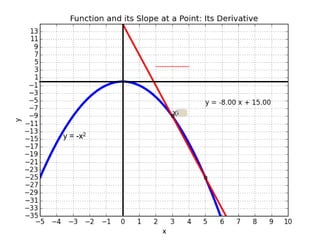
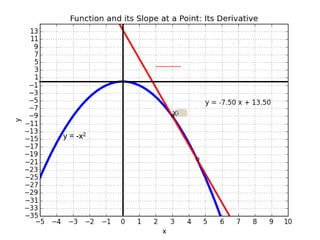
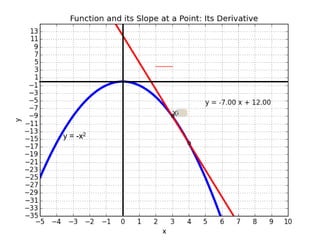
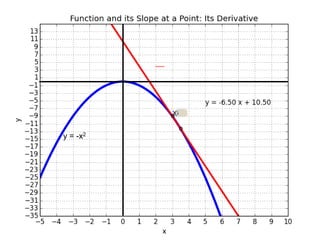
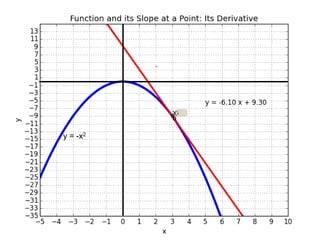
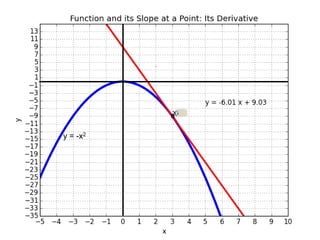
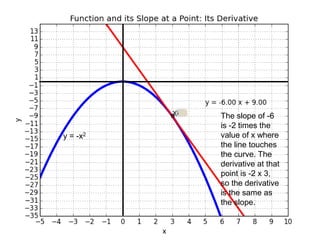
This document introduces basic differential calculus concepts focused on slopes of lines, specifically using the equation y=mx+b. It illustrates the relationship between a curve, such as y=-x^2, and its slope, leading to the understanding that the derivative at any point is -2 times the x-value at that point. The document encourages practicing similar steps with other functions like y=x^3 to solidify comprehension of calculus principles.

1. Introduction to Differential
Calculus
 Basic differential calculus for algebra students who are
becoming familiar with the concept of the slopes of lines.
 Slides by Paul E. Roundy, November 29, 2015

2. 
Review: Find the slope of this
line.

3. 
Run

4. 
RunRise

5. 
Run = -2Rise=12

6. 
Run = -2Rise=12
Slope = 12/-2 = -6

7. 
Run = -2Rise=12
Slope = 12/-2 = -6
Remember that it is the
same as m in the slope
intercept version of the
equation for the line (given
above, y=mx+b)

8. 
Run = -2Rise=12
o
Add downward opening parabola y=-x2
Now, add the curve y=-
x2 to the diagram.
Notice that this curve
touches the line y=-6x+9
at exactly one point,
x=3, y=-9.

9. y = -x2
To make the remaining steps easier,
I moved the axis range of the graph.

10. y = -x2
x
Next, I create a new line
that touches the curve at
two points. The line I
drew uses x=3 as the
first point and x=3+2, or
x=5 for the second point.

11. y = -x2
x
Yet, the point x could be
anything, and the shift to
the right of 3 (which I call
h) could be any shift
from x, so we will find
the slope of any such
line by letting x and h
take on any value.

12. y = -x2
x
-x2

13. y = -x2
x x+h
-x2
-(x+h)2

14. y = -x2
x x+h
-x2
-(x+h)2
So, what is the
slope of the
heavy red line
for any value of
h?

15. y = -x2
x x+h
-x2
-(x+h)2
Rise/Run

16. y = -x2
x x+h
-x2
-(x+h)2
Rise is top
minus bottom:
-x2
--
x+h( )
2

17. y = -x2
x x+h
-x2
-(x+h)2
Run is just
x+h-x, or h

18. y = -x2
x x+h
-x2
-(x+h)2
So rise over
run is

19. y = -x2
x x+h
-x2
-(x+h)2
So rise over
run is
-x2
--
x2
+ 2xh+ h2
( )
h

20. y = -x2
x x+h
-x2
-(x+h)2
So rise over
run is

21. y = -x2
x x+h
-x2
-(x+h)2
Now, think
about what
happens if we
let h shrink to
zero. The slope
of the line is
just

22. y = -x2

23. y = -x2

24. y = -x2

25. y = -x2

26. y = -x2

27. y = -x2

28. y = -x2
The slope of -6
is -2 times the
value of x where
the line touches
the curve. The
derivative at that
point is -2 x 3,
so the derivative
is the same as
the slope.

29. Congratulations!
 You have found the “derivative” of the curve y = -x2. It is -
2x. That means that no matter at what single point the
line touches the curve, its slope will be -2 times the value
of x at that point.
 Try the steps again for other functions, such as y = x3.
 The algebra will be more complicated, but the steps are the
same. The result for y=x3 is 3x2.